2023-2024学年初中数学九年级上册 25.3 解直角三角形 同步分层训练培优卷(沪教版五四制)
试卷更新日期:2023-07-29 类型:同步测试
一、选择题
-
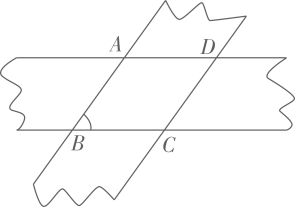
1. 如图,将两条宽度都为1的纸条重叠在一起,使 , 则四边形的面积为( )
 A、 B、 C、 D、2. 如图所示,在中,按以下步骤作图:①连接 , 以点C为圆心,以长为半径作弧,交于点F;②分别以点D,F为圆心,以长为半径作弧,两弧相交于点G;③作射线交于点E.若 , , 则的长为( )
A、 B、 C、 D、2. 如图所示,在中,按以下步骤作图:①连接 , 以点C为圆心,以长为半径作弧,交于点F;②分别以点D,F为圆心,以长为半径作弧,两弧相交于点G;③作射线交于点E.若 , , 则的长为( ) A、4 B、 C、 D、3. 如图,正方形的对角线 , 相交于点 , 平分交于点 , 若 , 则线段的长为( )
A、4 B、 C、 D、3. 如图,正方形的对角线 , 相交于点 , 平分交于点 , 若 , 则线段的长为( ) A、 B、 C、 D、4. 如图,在中, , 设所对的边边长分别为a,b,c,则下列等式正确的是( )
A、 B、 C、 D、4. 如图,在中, , 设所对的边边长分别为a,b,c,则下列等式正确的是( )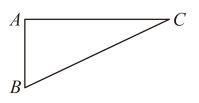 A、 B、 C、 D、5. 一沙滩球网支架示意图如图所示,AB=AC=a米,∠ABC=a,则最高点A离地面BC的高度为( )
A、 B、 C、 D、5. 一沙滩球网支架示意图如图所示,AB=AC=a米,∠ABC=a,则最高点A离地面BC的高度为( ) A、米 B、米 C、米 D、米6. 如图,在正方形中,点分别是上的动点,且 , 垂足为 , 将沿翻折,得到交于点 , 对角线交于点 , 连接 , 下列结论正确的是:①;②;③若 , 则四边形是菱形;④当点运动到的中点,;⑤ . ( )
A、米 B、米 C、米 D、米6. 如图,在正方形中,点分别是上的动点,且 , 垂足为 , 将沿翻折,得到交于点 , 对角线交于点 , 连接 , 下列结论正确的是:①;②;③若 , 则四边形是菱形;④当点运动到的中点,;⑤ . ( ) A、①②③④⑤ B、①②③⑤ C、①②③ D、①②⑤7. 在平面直角坐标系中,点A在直线l上,以A为圆心,为半径的圆与y轴的另一个交点为E,给出如下定义:若线段 , 和直线l上分别存在点B,点C和点D,使得四边形是矩形(点顺时针排列),则称矩形为直线l的“理想矩形”.例如,右图中的矩形为直线l的“理想矩形”.若点 , 则直线的“理想矩形”的面积为( )
A、①②③④⑤ B、①②③⑤ C、①②③ D、①②⑤7. 在平面直角坐标系中,点A在直线l上,以A为圆心,为半径的圆与y轴的另一个交点为E,给出如下定义:若线段 , 和直线l上分别存在点B,点C和点D,使得四边形是矩形(点顺时针排列),则称矩形为直线l的“理想矩形”.例如,右图中的矩形为直线l的“理想矩形”.若点 , 则直线的“理想矩形”的面积为( )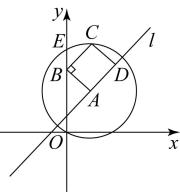 A、12 B、 C、 D、8. 赵爽弦图由四个全等的直角三角形所组成,形成一个大正方形,中间是一个小正方形(如图所示).某次课后服务拓展学习上,小浔绘制了一幅赵爽弦图,她将EG延长交CD于点I.记小正方形EFGH的面积为S1 , 大正方形ABCD的面积为S2 , 若DI=2,CI=1,S2=5S1 , 则GI的值是( )
A、12 B、 C、 D、8. 赵爽弦图由四个全等的直角三角形所组成,形成一个大正方形,中间是一个小正方形(如图所示).某次课后服务拓展学习上,小浔绘制了一幅赵爽弦图,她将EG延长交CD于点I.记小正方形EFGH的面积为S1 , 大正方形ABCD的面积为S2 , 若DI=2,CI=1,S2=5S1 , 则GI的值是( ) A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
9. 在中, , , 则 .10. 如图,在菱形中,对角线与交于点O,已知 , , 如果点E是边的中点,那么 .
 11. 一副直角三角板如图放置,点在的延长线上, , 则°.
11. 一副直角三角板如图放置,点在的延长线上, , 则°.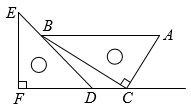 12. 如图,在等边中,过点C作射线 , 点M,N分别在边 , 上,将沿折叠,使点B落在射线上的点处,连接 , 已知 . 给出下列四个结论:①为定值;②当时,四边形为菱形;③当点N与C重合时,;④当最短时, . 其中正确的结论是(填写序号)
12. 如图,在等边中,过点C作射线 , 点M,N分别在边 , 上,将沿折叠,使点B落在射线上的点处,连接 , 已知 . 给出下列四个结论:①为定值;②当时,四边形为菱形;③当点N与C重合时,;④当最短时, . 其中正确的结论是(填写序号) 13. 如图,将平行四边形沿着对角线翻折,点的对应点为 , 交于点 , 如果 , , 且 , 那么平行四边形的周长为 .(参考数据:)
13. 如图,将平行四边形沿着对角线翻折,点的对应点为 , 交于点 , 如果 , , 且 , 那么平行四边形的周长为 .(参考数据:)
三、解答题
-
14. 如图,在中,已知 . 点为边上一点, , 求的长.
 15. 中, , , , 求边的长度.
15. 中, , , , 求边的长度.
四、综合题
-
16. 如图1,在菱形中, . 等腰的两个顶点分别在上,且 , 点在的异侧.
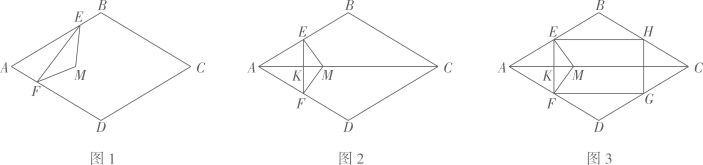 (1)、如图2,当于点时,
(1)、如图2,当于点时,①求证: , 且点在菱形的对角线上.
②如图3,若交于点交于点 , 连结 . 当 时,四边形为正方形.
(2)、如图1,①判断:点 ▲ 菱形的对角线上.(填“在”或“不在”)
②若 , 请求出的取值范围.
17. 问题情境:“综合与实践”课上,老师提出如下问题:将图1中的矩形纸片沿对角线剪开,得到两个全等的三角形纸片,表示为和 , 其中 . 将和按图2所示方式摆放,其中点与点重合(标记为点).当时,延长交于点 . 试判断四边形的形状,并说明理由.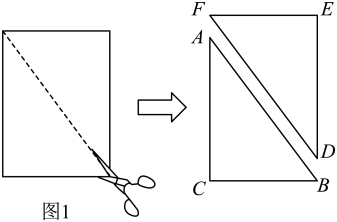 (1)、数学思考:谈你解答老师提出的问题;(2)、深入探究:老师将图2中的绕点逆时针方向旋转,使点落在内部,并让同学们提出新的问题.
(1)、数学思考:谈你解答老师提出的问题;(2)、深入探究:老师将图2中的绕点逆时针方向旋转,使点落在内部,并让同学们提出新的问题.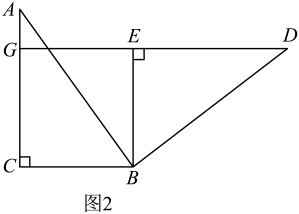
①“善思小组”提出问题:如图3,当时,过点作交的延长线于点与交于点 . 试猜想线段和的数量关系,并加以证明.请你解答此问题;
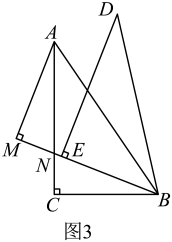
②“智慧小组”提出问题:如图4,当时,过点作于点 , 若 , 求的长.请你思考此问题,直接写出结果.