2023-2024学年初中数学九年级上册 25.2 求锐角三角比的值同步分层训练培优卷(沪教版五四制)

试卷更新日期：2023-07-29 类型：同步测试

进入出卷网下载

一、选择题

1. 已知“ $α$ 为锐角时， $s i n α$ 随着 $α$ 的增大而增大”，则 $s i n 37 °$ 的值更靠近（）

A、 $\frac{2}{5}$ B、 $\frac{3}{5}$ C、 $\frac{4}{5}$ D、 $\frac{5}{6}$

查看试题解析
2. 在 $R t △ A B C$ 中， $∠ C = 90 °$ ，若 $c o s A = \frac{1}{2}$ ，则 $∠ A$ 的大小是（）

A、 $30 °$ B、 $45 °$ C、 $60 °$ D、 $75 °$

查看试题解析
3. 下列各式中，运算结果是分数的是（）

A、 $s i n 30 °$ B、 ${(\frac{π}{2})}^{0}$ C、 ${(\frac{1}{2})}^{- 1}$ D、 $\sqrt{\frac{3}{4}}$

查看试题解析
4. 如图，在平面直角坐标系中， $R t △ A B O$ 的顶点 $B$ 在 $x$ 轴的正半轴上， $∠ A B O = 90 °$ ，点 $A$ 的坐标为 $(1 ， \sqrt{3})$ ，将 $△ A B O$ 绕点 $O$ 逆时针旋转，使点 $B$ 的对应点 $B^{'}$ 落在边 $O A$ 上，连接 $A$ 、 $A^{'}$ ，则线段 $A A^{'}$ 的长度是（）

A、1 B、2 C、 $\sqrt{3}$ D、 $2 \sqrt{3}$

查看试题解析
5. 在直角三角形ABC中， $∠ C = 90 ° ， A B = 4 ， B C = 2 \sqrt{3}$ ，则 $3 t a n \frac{A}{2}$ 的值是（）

A、 $\sqrt{3}$ B、 $2 \sqrt{3}$ C、 $3 \sqrt{3}$ D、3

查看试题解析
6. $y = \sqrt{3} x$ 与 $y = \frac{k}{x}$ 交于A、B两点， $A C ⊥ A B$ 交y轴于点C， $B C$ 延长线交双曲线于点D，若 $B D = 5$ ，则 $A D$ 为（）

A、2 B、3 C、 $\sqrt{3}$ D、 $\frac{5}{3} \sqrt{3}$

查看试题解析
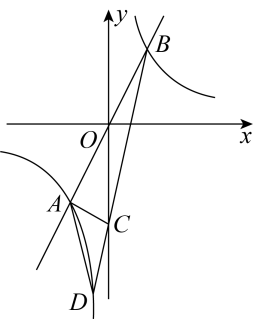7. 如图，在平行四边形OABC中，边OC在x轴上，点A（1， $\sqrt{3}$ ），点C（3，0）．按以下步骤作图：分别以点B，C为圆心，大于 $\frac{1}{2}$ BC的长为半径作弧，两弧相交于E，F两点；作直线EF，交AB于点H；连接OH，则OH的长为（）

A、 $\sqrt{5}$ B、 $\sqrt{7}$ C、2 $\sqrt{2}$ D、2 $\sqrt{2}$

查看试题解析
8. 如图坐标系中，O（0，0），A（3，3 $\sqrt{3}$ ），B（6，0），将△OAB沿直线CD折叠，使点A恰好落在线段OB上的点E处，若OE＝ $\frac{6}{5}$ ，则AC：AD的值是（）

A、1：2 B、2：3 C、6：7 D、7：8

查看试题解析

二、填空题

9. 如图，已知在 $△ A B C$ 中， $A B = 7 ， ∠ A C B = 120 °$ ，将 $△ A B C$ 绕点B顺时针旋转 $60 °$ ，点 $A 、 C$ 分别落在点 $D 、 E$ 处，联结 $D C$ ，如果 $D C ⊥ A C$ ，那么边 $B C$ 的长．

查看试题解析
10. 如图，已知在矩形 $A B C D$ 中，点 $E$ 在边 $B C$ 上， $B E = 2 C E$ ，将矩形沿着过点 $E$ 的直线翻折后，点 $C ， D$ 分别落在边 $B C$ 下方的点 $C^{'} ， D^{'}$ 处，且点 $C^{'} ， D^{'} ， B$ 在同一条直线上，折痕与边 $A D$ 交于点 $F ， D^{'} F$ 与 $B E$ 交于点 $G$ ．设 $A B = \sqrt{3}$ ，那么 $△ E F G$ 的周长为．

查看试题解析
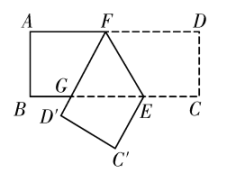11. 如图，在正方形 $A B C D$ 中，点E、F分别在边 $A D 、 A B$ 上， $E F ⊥ C E$ ．将 $△ C D E$ 沿直线CE翻折，如果点D的对应点恰好落在线段 $C F$ 上，那么 $∠ E F C$ 的正切值是．

查看试题解析
12. 如图，在锐角三角形ABC中，tanA= $\sqrt{3}$ ， BC= $\sqrt{5}$ ，线段BD、CE分别是AC、AB边上的高线，连接DE，则三角形ADE面积的最大值是

查看试题解析
13. 如图，在正方形 $A B C D$ 内部作等边 $△ E D C$ ， $A E$ 交 $B C$ 于F点，过E作 $G H ⊥ A F$ ，分别交 $A B 、 C D$ 于点G，H．则 $\frac{E H}{A F}$ 的值是．

查看试题解析

三、计算题

14. 计算： ${(\frac{1}{3})}^{- 2} + t a n 45 ° - \sqrt{{(- 10)}^{2}}$ ．

查看试题解析

四、解答题

15. 先化简，再求代数式 $(\frac{1}{x + 1} - \frac{1}{x - 1}) \div \frac{x + 1}{x^{2} + 2 x + 1}$ 的值，其中 $x = 3 t a n 30 ° + \sqrt{2} c o s 45 °$ ．

查看试题解析
16. 小岛A在港口P的南偏西45°方向，距离港口81海里处．甲船从 $A$ 出发，沿 $A P$ 方向以6海里/时的速度驶向港口，乙船从港口 $P$ 出发，沿南偏东60°方向，以15海里/时的速度驶离港口．现两船同时出发．

(1)、出发后小时两船与港口 $P$ 的距离相等；

(2)、出发几小时后乙船在甲船的正东方向?（结果精确到0.1小时，参考数据： $\sqrt{2} = 1.41 ， \sqrt{3} = 1.73)$

查看试题解析

五、综合题

17. 如图，在菱形ABCD中，对角线AC，BD相交于点 $O$ ，点P，Q分别是边BC，线段OD上的点，连接AP，QP，AP与OB相交于点 $E$ .

(1)、如图1，连接QA.当 $Q A = Q P$ 时，试判断点 $Q$ 是否在线段PC的垂直平分线上，并说明理由；

(2)、如图2， $∠ A P B = 9 0^{°}$ ，且 $∠ B A P = ∠ A D B$ ，
①求证： $A E = 2 E P$ ；

②当 $O Q = O E$ 时，设 $E P = a$ ，求PQ的长（用含a的代数式表示）.

查看试题解析
18. 如图，平行四边形 $A B C D$ 中， $A E 、 C F$ 分别是 $∠ B A D 、 ∠ B C D$ 的平分线，且 $E 、 F$ 分别在边 $B C 、 A D$ 上， $A E = A F$ ．

(1)、求证：四边形 $A E C F$ 是菱形；

(2)、若 $∠ A B C = 60 °$ ， $△ A B E$ 的面积等于 $4 \sqrt{3}$ ，求平行线 $A B$ 与 $D C$ 间的距离．

查看试题解析

2023-2024学年初中数学九年级上册 25.2 求锐角三角比的值 同步分层训练培优卷(沪教版五四制)

一、选择题

二、填空题

三、计算题

四、解答题

五、综合题

2023-2024学年初中数学九年级上册 25.2 求锐角三角比的值同步分层训练培优卷(沪教版五四制)