2023-2024学年初中数学九年级上册 25.1 锐角三角比的意义 同步分层训练基础卷(沪教版五四制)
试卷更新日期:2023-07-29 类型:同步测试
一、选择题
-
1. 如图,在中, , , , 则的值为( )
 A、 B、 C、 D、2. 在Rt△ABC中,∠C=90°,AC=4,AB=5,则cosA的值为( )A、 B、 C、 D、3. Rt△ABC中,若∠C=90°,BC=3,AC=4,则cosA的值为( )A、 B、 C、 D、4. 在中, , 若 , 则的值为( )A、 B、 C、2 D、5. 如图1是第七届国际数学教育大会()的会徽,在其主体图案中选择两个相邻的直角三角形,恰好能组合得到如图所示的四边形.如果已知 , , 则的值是( )
A、 B、 C、 D、2. 在Rt△ABC中,∠C=90°,AC=4,AB=5,则cosA的值为( )A、 B、 C、 D、3. Rt△ABC中,若∠C=90°,BC=3,AC=4,则cosA的值为( )A、 B、 C、 D、4. 在中, , 若 , 则的值为( )A、 B、 C、2 D、5. 如图1是第七届国际数学教育大会()的会徽,在其主体图案中选择两个相邻的直角三角形,恰好能组合得到如图所示的四边形.如果已知 , , 则的值是( ) A、 B、 C、 D、6. 如图,在中, , , , 则( )
A、 B、 C、 D、6. 如图,在中, , , , 则( )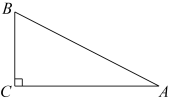 A、 B、 C、4 D、7. 如图,已知正方形ABCD的边长为2,点E、F分别为AB、BC边的中点,连接AF、DE相交于点M,则∠CDM等于( )
A、 B、 C、4 D、7. 如图,已知正方形ABCD的边长为2,点E、F分别为AB、BC边的中点,连接AF、DE相交于点M,则∠CDM等于( ) A、 B、 C、 D、8. 如图,在中, , 若 , , 点是上一点,且 , 则的值为( ).
A、 B、 C、 D、8. 如图,在中, , 若 , , 点是上一点,且 , 则的值为( ).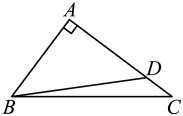 A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
9. 如图,在中, , 点D为边的中点,连接 , 若 , 则的值是.
 10. 如图,AB与CD相交于点O,AC⊥CD于点C,BD⊥CD于点D,若AC=10,OC=15,则的值为 .
10. 如图,AB与CD相交于点O,AC⊥CD于点C,BD⊥CD于点D,若AC=10,OC=15,则的值为 . 11. 如图,Rt△ABC中, , AC=5,BC=12,则cosA的值为 .
11. 如图,Rt△ABC中, , AC=5,BC=12,则cosA的值为 .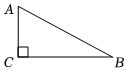 12. 如图,在一张长方形纸片中, 点 , 分别是和的中点,点是上一点,将矩形的一角沿所在的直线翻折,点恰好落在上,若 , 则的长是.
12. 如图,在一张长方形纸片中, 点 , 分别是和的中点,点是上一点,将矩形的一角沿所在的直线翻折,点恰好落在上,若 , 则的长是. 13. 图1是一种折叠式晾衣架展开时的情况,图2是示意图,两个支脚和晾衣臂 , 张开夹角 , 晾衣臂支架.
13. 图1是一种折叠式晾衣架展开时的情况,图2是示意图,两个支脚和晾衣臂 , 张开夹角 , 晾衣臂支架. (1)、当时,的度数为.(2)、当OC从水平方向旋转到时,的面积为.
(1)、当时,的度数为.(2)、当OC从水平方向旋转到时,的面积为.三、解答题
-
14. 求出图中∠A的正弦值、余弦值和正切值.
 15. 为了充分利用四边形余料,小明设计了不同的方案裁剪正方形,裁剪方案与数据如下表:
15. 为了充分利用四边形余料,小明设计了不同的方案裁剪正方形,裁剪方案与数据如下表:方案设计
方案1
方案2
裁剪方案示意图


说明
图中的正方形和正方形四个顶点都在原四边形的边上
测量数据
, , , ;
任务1:探寻边角
填空: ▲ , ▲ ;
任务2:比较面积
计算或推理:正方形和正方形边长之比;
任务3:应用实践
若在余料上再截取一个最大正方形,正方形的边长为 ▲ .
四、作图题
-
16. 如图,在平面直角坐标系中,的顶点坐标分别为 , , .
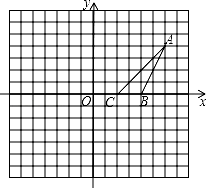 (1)、在y轴左侧,以O为位似中心,画出 , 使它与的相似比为;(2)、根据(1)的作图,.
(1)、在y轴左侧,以O为位似中心,画出 , 使它与的相似比为;(2)、根据(1)的作图,.五、综合题
-
17. 在和中,点在同一直线上,.
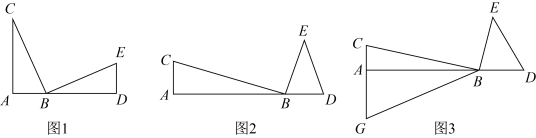 (1)、如图1,如果 , 求证:;(2)、如果 , , .
(1)、如图1,如果 , 求证:;(2)、如果 , , .如图2,当时,求的长;
如图3,点是延长线上一点,且 , 连结 , 如果 , 求的值.
18. 我们知道:如图①,点B把线段AC分成两部分,如果= , 那么称点B为线段AC的黄金分割点.它们的比值为.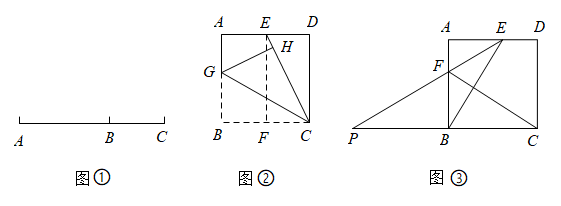 (1)、在图①中,若AC=20cm,则AB的长为cm;(2)、如图②,用边长为20cm的正方形纸片进行如下操作:对折正方形ABCD得折痕EF,连接CE,将CB折叠到CE上,点B对应点H,得折痕CG.试说明:G是AB的黄金分割点;(3)、如图③,小明进一步探究:在边长为a的正方形ABCD的边AD上任取点E(AE>DE),连接BE,作CF⊥BE,交AB于点F,延长EF、CB交于点P.他发现当PB与BC满足某种关系时,E、F恰好分别是AD、AB的黄金分割点.请猜想小明的发现,并说明理由.
(1)、在图①中,若AC=20cm,则AB的长为cm;(2)、如图②,用边长为20cm的正方形纸片进行如下操作:对折正方形ABCD得折痕EF,连接CE,将CB折叠到CE上,点B对应点H,得折痕CG.试说明:G是AB的黄金分割点;(3)、如图③,小明进一步探究:在边长为a的正方形ABCD的边AD上任取点E(AE>DE),连接BE,作CF⊥BE,交AB于点F,延长EF、CB交于点P.他发现当PB与BC满足某种关系时,E、F恰好分别是AD、AB的黄金分割点.请猜想小明的发现,并说明理由.
-