2023-2024学年初中数学九年级上册 24.5 相似三角形的性质 同步分层训练培优卷(沪教版五四制)
试卷更新日期:2023-07-29 类型:同步测试
一、选择题
-
1. 如图所示, , , , 则的长为( )
 A、 B、2 C、3 D、42. 凸透镜成像的原理如图所示,.若物体到焦点的距离与焦点到凸透镜中心线的距离之比为 , 则物体被缩小到原来的( )
A、 B、2 C、3 D、42. 凸透镜成像的原理如图所示,.若物体到焦点的距离与焦点到凸透镜中心线的距离之比为 , 则物体被缩小到原来的( ) A、 B、 C、 D、3. 如图,E,F,G,H分别是矩形四条边上的点,已知 , 若 , , 则为( )
A、 B、 C、 D、3. 如图,E,F,G,H分别是矩形四条边上的点,已知 , 若 , , 则为( )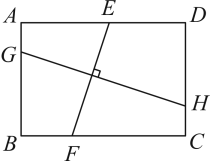 A、 B、 C、 D、4. 如图,线段 , 相交于点 , , 若 , , , 则的长是( )
A、 B、 C、 D、4. 如图,线段 , 相交于点 , , 若 , , , 则的长是( ) A、3 B、4 C、5 D、65. 如图,在中,点 , 分别在 , 上, , , 且 , , 则的长为( )
A、3 B、4 C、5 D、65. 如图,在中,点 , 分别在 , 上, , , 且 , , 则的长为( ) A、 B、4 C、5 D、6. 如图是一张矩形纸片 , 点E是中点,点F在上,把该纸片沿折叠,点A、B的对应点分别为、 , 与相交于点G,的延长线经过点C.若 , 则的值为( )
A、 B、4 C、5 D、6. 如图是一张矩形纸片 , 点E是中点,点F在上,把该纸片沿折叠,点A、B的对应点分别为、 , 与相交于点G,的延长线经过点C.若 , 则的值为( )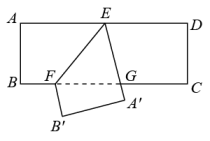 A、 B、 C、 D、7. 如图,在矩形中,点是边的三等分点 , 点是边的中点,线段 , 与对角线分别交于点 , .设矩形的面积为 , 则以下4个结论中:①;②;③;④.正确的结论有( )
A、 B、 C、 D、7. 如图,在矩形中,点是边的三等分点 , 点是边的中点,线段 , 与对角线分别交于点 , .设矩形的面积为 , 则以下4个结论中:①;②;③;④.正确的结论有( ) A、1个 B、2个 C、3个 D、4个8. 如图, , , , 分别是矩形四条边上的点,连接 , 相交于点 , 且 , , 矩形矩形 , 连接交 , 于点 , , 下列一定能求出面积的条件是( )
A、1个 B、2个 C、3个 D、4个8. 如图, , , , 分别是矩形四条边上的点,连接 , 相交于点 , 且 , , 矩形矩形 , 连接交 , 于点 , , 下列一定能求出面积的条件是( ) A、矩形和矩形的面积之差 B、矩形与矩形的面积之差 C、矩形和矩形的面积之差 D、矩形和矩形的面积之差
A、矩形和矩形的面积之差 B、矩形与矩形的面积之差 C、矩形和矩形的面积之差 D、矩形和矩形的面积之差二、填空题
-
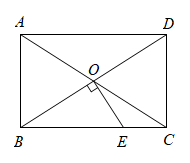
9. 如图,矩形的对角线 , 相交于点 , 过点作 , 交于点 , 若 , , 则的长为.
 10. 如图,在平面直角坐标系中, , 点A坐标是 , 若反比例函数的图像经过点B,则k的值为.
10. 如图,在平面直角坐标系中, , 点A坐标是 , 若反比例函数的图像经过点B,则k的值为. 11. 如图,面积为4的正方形中,分别是各边的中点,将一边两端点分别和对边中点连结,所得阴影部分为各边相等的八边形,则八边形每条边的长度是.
11. 如图,面积为4的正方形中,分别是各边的中点,将一边两端点分别和对边中点连结,所得阴影部分为各边相等的八边形,则八边形每条边的长度是. 12. 如图,菱形ABCD的边长为4,∠BAD=60°,点E是边AB上一动点(不与点A、B重合),过点E作EF∥BC交AC于点F,连接DF,当△ADF是等腰三角形时,AE的长为.
12. 如图,菱形ABCD的边长为4,∠BAD=60°,点E是边AB上一动点(不与点A、B重合),过点E作EF∥BC交AC于点F,连接DF,当△ADF是等腰三角形时,AE的长为. 13. 已知过原点的一条直线与反比例函数的图象交于 , 两点在的右侧.是反比例函数图象上位于点上方的一动点,连接并延长交轴于点 , 连接交轴于点.若 , 则.
13. 已知过原点的一条直线与反比例函数的图象交于 , 两点在的右侧.是反比例函数图象上位于点上方的一动点,连接并延长交轴于点 , 连接交轴于点.若 , 则.三、解答题
-
14. 雯雯和笑笑想利用皮尺和所学的几何知识测量学校操场上旗杆的高度,他们的测量方案如下:当雯雯站在旗杆正前方地面上的点D处时,笑笑在地面上找到一点G,使得点G、雯雯的头顶C以及旗杆的顶部A三点在同一直线上,并测得DG=2.8m;然后雯雯向前移动1.5m到达点F处,笑笑同样在地面上找到一点H,使得点H、雯雯的头顶E以及旗杆的顶部A三点在同一直线上,并测得GH=1.7m,已知图中的所有点均在同一平面内,AB⊥BH,CD⊥BH,EF⊥BH,雯雯的身高CD=EF=1.6m.请你根据以上测量数据,求该校旗杆的高度AB.
 15. 如图,乐乐测得学校门口栏杆的短臂长1米,长臂长4米,当短臂外端A下降米时,求长臂外端B升高多少米?
15. 如图,乐乐测得学校门口栏杆的短臂长1米,长臂长4米,当短臂外端A下降米时,求长臂外端B升高多少米?
四、作图题
-
16. 在平面直角坐标系中的位置如图所示,已知点 , , .与是以点P为位似中心的位似图形.

( 1 )请画出点P的位置,并写出点P的坐标是____;
( 2 )以点O为位似中心,在y轴左侧画出△ABC的位似图形 , 使相似比为1:1.五、综合题
-
17. 如图
 (1)、模型建立:如图1,在△ABC中,D是AB上一点,∠ACD=∠B,求证:AC²=AD·AB;(2)、类比探究:如图2,在菱形ABCD中,E、F分别为边BC、DC上的点,且 射线AE交DC的延长线于点M,射线AF交BC的延长线于点N.
(1)、模型建立:如图1,在△ABC中,D是AB上一点,∠ACD=∠B,求证:AC²=AD·AB;(2)、类比探究:如图2,在菱形ABCD中,E、F分别为边BC、DC上的点,且 射线AE交DC的延长线于点M,射线AF交BC的延长线于点N.①求证:. FA2=FC · FM
②若AF=4,CF=2,AM=10,求FN的长.
18. 如图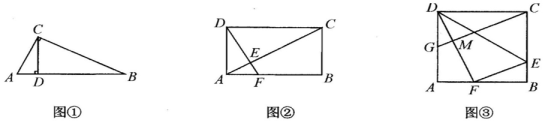 (1)、[基础巩固]如图①,在Rt△ABC中,∠ACB=90°,CD⊥AB于点D,求证:AC2 =AD·AB.(2)、[尝试应用] 如图②,在矩形ABCD中,AD=2,点F在AB上,FB=2AF,DF⊥AC于点E,求AE的长.(3)、[拓展提高] 如图③,在矩形ABCD中,点E在边BC上,NDCE与NDFE关于直线DE对称,点C的对称点F在边AB上,G为AD中点,连结GC交DF于点M,GC∥FE,若AD=2,求GM的长.
(1)、[基础巩固]如图①,在Rt△ABC中,∠ACB=90°,CD⊥AB于点D,求证:AC2 =AD·AB.(2)、[尝试应用] 如图②,在矩形ABCD中,AD=2,点F在AB上,FB=2AF,DF⊥AC于点E,求AE的长.(3)、[拓展提高] 如图③,在矩形ABCD中,点E在边BC上,NDCE与NDFE关于直线DE对称,点C的对称点F在边AB上,G为AD中点,连结GC交DF于点M,GC∥FE,若AD=2,求GM的长.
-