2023-2024学年初中数学九年级上册 24.3 三角形一边的平行线 同步分层训练培优卷(沪教版五四制)
试卷更新日期:2023-07-29 类型:同步测试
一、选择题
-
1. 某校要举办国庆联欢会,主持人站在舞台中轴线AB的黄金分割点C处(如图1)最自然得体.即 , 在数轴(如题图2)上最接近的点是( )
 A、 B、 C、 D、2. 如图,在中,点D在边上,过点D作 , 交于点E.若 , 则的值是( )
A、 B、 C、 D、2. 如图,在中,点D在边上,过点D作 , 交于点E.若 , 则的值是( ) A、 B、 C、 D、3. 我国著名数学家华罗庚曾为普及优选法作出重要贡献,优选法中有一种0.618法应用了( )A、黄金分割数 B、平均数 C、众数 D、中位数4. 小明用地理中所学的等高线的知识在某地进行野外考察,他根据当地地形画出了“等高线示意图”,如图所示(注:若某地在等高线上,则其海拔就是其所在等高线的数值;若不在等高线上,则其海拔在相邻两条等高线的数值范围内),若点 , , 三点均在相应的等高线上,且三点在同一直线上,则的值为( )
A、 B、 C、 D、3. 我国著名数学家华罗庚曾为普及优选法作出重要贡献,优选法中有一种0.618法应用了( )A、黄金分割数 B、平均数 C、众数 D、中位数4. 小明用地理中所学的等高线的知识在某地进行野外考察,他根据当地地形画出了“等高线示意图”,如图所示(注:若某地在等高线上,则其海拔就是其所在等高线的数值;若不在等高线上,则其海拔在相邻两条等高线的数值范围内),若点 , , 三点均在相应的等高线上,且三点在同一直线上,则的值为( ) A、 B、 C、 D、25. 如图,在矩形中, , 延长至点 , 使得 , 以为直径的半圆交延长线于点.欧几里得在《几何原本》中利用该图得到结论:矩形的面积等于的平方(即).现连接并延长交于点 , 若 , 则与矩形的面积之比为( )
A、 B、 C、 D、25. 如图,在矩形中, , 延长至点 , 使得 , 以为直径的半圆交延长线于点.欧几里得在《几何原本》中利用该图得到结论:矩形的面积等于的平方(即).现连接并延长交于点 , 若 , 则与矩形的面积之比为( )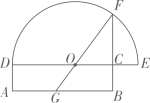 A、 B、 C、 D、6. 在中,点D、E分别在AB、AC上,如果AD::3,那么下列条件中能够判断的是( )A、 B、 C、 D、7. 如图,在矩形ABCD的外部有四个全等的直角三角形,分别为△AEB,△BFG,△CGD,△DHE,连结EC,DF交于点O,若 , 则的值为( )
A、 B、 C、 D、6. 在中,点D、E分别在AB、AC上,如果AD::3,那么下列条件中能够判断的是( )A、 B、 C、 D、7. 如图,在矩形ABCD的外部有四个全等的直角三角形,分别为△AEB,△BFG,△CGD,△DHE,连结EC,DF交于点O,若 , 则的值为( )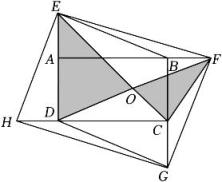 A、 B、 C、 D、8. 如图,边长为5的大正方形是由四个全等的直角三角形和一个小正方形组成,连结并延长交于点M.若 , 则的长为( )
A、 B、 C、 D、8. 如图,边长为5的大正方形是由四个全等的直角三角形和一个小正方形组成,连结并延长交于点M.若 , 则的长为( ) A、 B、 C、1 D、
A、 B、 C、1 D、二、填空题
-
9. 如图,直线AD,BC交于点O,.若 , , .则的值为 .
 10. 如图,在四边形中, , 对角线相交于点 . 若 , 则的长为 .
10. 如图,在四边形中, , 对角线相交于点 . 若 , 则的长为 .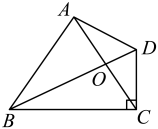 11. 如图,正方形中,E为上一点,过B作于G,延长至点F使 , 延长交于点M,连接 , 若C为中点, , 则的长为 .
11. 如图,正方形中,E为上一点,过B作于G,延长至点F使 , 延长交于点M,连接 , 若C为中点, , 则的长为 . 12. 由四个全等的直角三角形和一个小正方形组成的大正方形ABCD如图所示.将小正方形对角线EF双向延长,分别交边AB,和边BC的延长线于点G,H.若大正方形与小正方形的面积之比为5,GH=2 , 则大正方形的边长为 .
12. 由四个全等的直角三角形和一个小正方形组成的大正方形ABCD如图所示.将小正方形对角线EF双向延长,分别交边AB,和边BC的延长线于点G,H.若大正方形与小正方形的面积之比为5,GH=2 , 则大正方形的边长为 . 13. 如图,在平行四边形ABCD中, , , ,分别以A,C为圆心,大于 的长为半径画弧,两弧相交于点M,N,过M,N两点作直线,与BC交于点E,与AD交于点F,连接AE,CF,则四边形AECF的周长为.
13. 如图,在平行四边形ABCD中, , , ,分别以A,C为圆心,大于 的长为半径画弧,两弧相交于点M,N,过M,N两点作直线,与BC交于点E,与AD交于点F,连接AE,CF,则四边形AECF的周长为.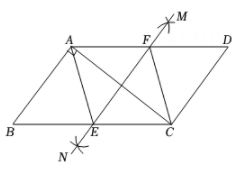
三、解答题
-
14. 如图,在中, , 若 , 求的长.
 15. 如图,梯形中, , 点E是边的中点,联结并延长交的延长线于点F,交于点G.求证: .
15. 如图,梯形中, , 点E是边的中点,联结并延长交的延长线于点F,交于点G.求证: .
四、作图题
-
16. 如图,在由边长都为1的小正方形组成的网格中,点 均为格点,点 为线段 上的动点,且满足 .

(Ⅰ)当点Q为线段 中点时 的长度等于 ▲ .
(Ⅱ)当线段 取得最小值时,请借助无刻度直尺在给定的网格中画出点Q,并简要说明你是怎么画出点Q的.
五、综合题
-
17. 课本再现
思考
我们知道,菱形的对角线互相垂直.反过来,对角线互相垂直的平行四边形是菱形吗?
可以发现并证明菱形的一个判定定理;
对角线互相垂直的平行四边形是菱形.
(1)、定理证明:为了证明该定理,小明同学画出了图形(如图1),并写出了“已知”和“求证”,请你完成证明过程.已知:在中,对角线 , 垂足为 .
求证:是菱形.
 (2)、知识应用:如图 , 在中,对角线和相交于点 , .
(2)、知识应用:如图 , 在中,对角线和相交于点 , .
①求证:是菱形;
②延长至点 , 连接交于点 , 若 , 求的值.
18. 如图,在的方格纸中,请按要求画格点线段(端点在格点上),且线段的端点均不与点A,B,C,D重合. (1)、在图1中画一条格点线段 , 使G,H分别落在边 , 上,且与互相平分.(2)、在图2上画一条格点线段 , 使M,N分别落在边 , 上,且要求分为两部分.
(1)、在图1中画一条格点线段 , 使G,H分别落在边 , 上,且与互相平分.(2)、在图2上画一条格点线段 , 使M,N分别落在边 , 上,且要求分为两部分.
-