2023-2024学年初中数学九年级上册 24.3 三角形一边的平行线 同步分层训练基础卷(沪教版五四制)
试卷更新日期:2023-07-29 类型:同步测试
一、选择题
-
1. 如图,五线谱是由等距离、等长度的五条平行横线组成的,同一条直线上的三个点A,B,C都在横线上,若线段 , 则线段的长是( )
 A、 B、 C、 D、22. 如图, , 则下列比例式成立的是( )
A、 B、 C、 D、22. 如图, , 则下列比例式成立的是( )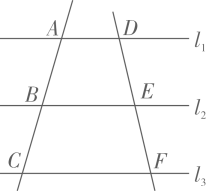 A、 B、 C、 D、3. 某校要举办国庆联欢会,主持人站在舞台中轴线AB的黄金分割点C处(如图1)最自然得体.即 , 在数轴(如题图2)上最接近的点是( )
A、 B、 C、 D、3. 某校要举办国庆联欢会,主持人站在舞台中轴线AB的黄金分割点C处(如图1)最自然得体.即 , 在数轴(如题图2)上最接近的点是( ) A、 B、 C、 D、4. 如图,在中,点D在边上,过点D作 , 交于点E.若 , 则的值是( )
A、 B、 C、 D、4. 如图,在中,点D在边上,过点D作 , 交于点E.若 , 则的值是( ) A、 B、 C、 D、5. 我国著名数学家华罗庚曾为普及优选法作出重要贡献,优选法中有一种0.618法应用了( )A、黄金分割数 B、平均数 C、众数 D、中位数6. 小明用地理中所学的等高线的知识在某地进行野外考察,他根据当地地形画出了“等高线示意图”,如图所示(注:若某地在等高线上,则其海拔就是其所在等高线的数值;若不在等高线上,则其海拔在相邻两条等高线的数值范围内),若点 , , 三点均在相应的等高线上,且三点在同一直线上,则的值为( )
A、 B、 C、 D、5. 我国著名数学家华罗庚曾为普及优选法作出重要贡献,优选法中有一种0.618法应用了( )A、黄金分割数 B、平均数 C、众数 D、中位数6. 小明用地理中所学的等高线的知识在某地进行野外考察,他根据当地地形画出了“等高线示意图”,如图所示(注:若某地在等高线上,则其海拔就是其所在等高线的数值;若不在等高线上,则其海拔在相邻两条等高线的数值范围内),若点 , , 三点均在相应的等高线上,且三点在同一直线上,则的值为( ) A、 B、 C、 D、27. 在中,点D、E分别在AB、AC上,如果AD::3,那么下列条件中能够判断的是( )A、 B、 C、 D、8. 如图,在中,点分别在边上, , 若 , 则 ( )
A、 B、 C、 D、27. 在中,点D、E分别在AB、AC上,如果AD::3,那么下列条件中能够判断的是( )A、 B、 C、 D、8. 如图,在中,点分别在边上, , 若 , 则 ( ) A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
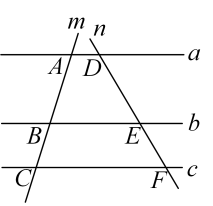
9. 若线段 , 点C是线段的一个黄金分割点(),则的长为(结果保留根号).10. 如图,直线 , 分别交直线、于点 , , , , , 若 , , 则的长为 .
 11. 如图,直线AD,BC交于点O,.若 , , .则的值为 .
11. 如图,直线AD,BC交于点O,.若 , , .则的值为 . 12. 如图,在四边形中, , 对角线相交于点 . 若 , 则的长为 .
12. 如图,在四边形中, , 对角线相交于点 . 若 , 则的长为 .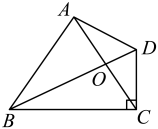 13. 如图,在菱形中,点E,F,G,H分别是 , , , 上的点,且 , 若菱形的面积等于24, , 则 .
13. 如图,在菱形中,点E,F,G,H分别是 , , , 上的点,且 , 若菱形的面积等于24, , 则 .
三、解答题
-
14. 如图,在中, , 若 , 求的长.
 15. 如图,梯形中, , 点E是边的中点,联结并延长交的延长线于点F,交于点G.求证: .
15. 如图,梯形中, , 点E是边的中点,联结并延长交的延长线于点F,交于点G.求证: .
四、作图题
-
16. 在的方格纸中,每个小正方形的边长为1,的顶点都是格点,请用无刻度的直尺作图.
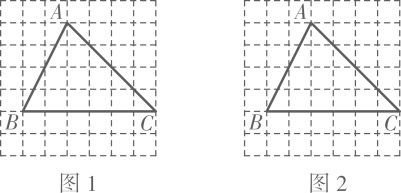 (1)、在图1中AB边上画点D,使得 .(2)、在图2中作的高CE.
(1)、在图1中AB边上画点D,使得 .(2)、在图2中作的高CE.五、综合题
-
17. 如图,在平面直角坐标系中,函数的图象与函数的图象相交于点A,并与轴交于点C,S△AOC=15.点D是线段AC上一点,CD:AC=2:3.
 (1)、求的值;(2)、求点D的坐标;(3)、根据图象,直接写出当时不等式的的解集.18. 课本再现
(1)、求的值;(2)、求点D的坐标;(3)、根据图象,直接写出当时不等式的的解集.18. 课本再现思考
我们知道,菱形的对角线互相垂直.反过来,对角线互相垂直的平行四边形是菱形吗?
可以发现并证明菱形的一个判定定理;
对角线互相垂直的平行四边形是菱形.
(1)、定理证明:为了证明该定理,小明同学画出了图形(如图1),并写出了“已知”和“求证”,请你完成证明过程.已知:在中,对角线 , 垂足为 .
求证:是菱形.
 (2)、知识应用:如图 , 在中,对角线和相交于点 , .
(2)、知识应用:如图 , 在中,对角线和相交于点 , .
①求证:是菱形;
②延长至点 , 连接交于点 , 若 , 求的值.
-