2023-2024学年初中数学八年级上册 19.9 勾股定理 同步分层训练培优卷(沪教版五四制)
试卷更新日期:2023-07-29 类型:同步测试
一、选择题
-
1. 如图,在△ABC中,AB=AC=10,BC=12,AD平分∠BAC,则AD等于( )
 A、6 B、7 C、8 D、92. 如图,以直角三角形的各边边长分别向外做等边三角形,再把较小的两个三角形按如图2的方式放置在最大的三角形内,是小梯形面积,是三个三角形重叠部分的面积,是大梯形的面积,是平行四边形的面积,则下列关系一定成立的是( )
A、6 B、7 C、8 D、92. 如图,以直角三角形的各边边长分别向外做等边三角形,再把较小的两个三角形按如图2的方式放置在最大的三角形内,是小梯形面积,是三个三角形重叠部分的面积,是大梯形的面积,是平行四边形的面积,则下列关系一定成立的是( ) A、 B、 C、 D、3. 如图,正方形ABCD的边长为10,AG=CH=8,BG=DH=6,则线段GH的长为( )
A、 B、 C、 D、3. 如图,正方形ABCD的边长为10,AG=CH=8,BG=DH=6,则线段GH的长为( )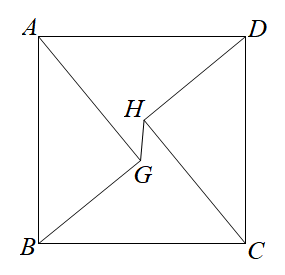 A、 B、 C、 D、4. 下列各组数据为三角形三边,能构成直角三角形的是( )A、 , , B、 , , C、 , , D、 , ,5. △ABC的三条边分别为a,b,c,下列条件不能判断△ABC是直角三角形的是( )A、a2+b2=c2 B、∠A=∠B+∠C C、∠A∶∠B∶∠C=3∶4∶5 D、a=5,b=12,c=136. 在下列条件中:①;②;③;④ , 能确定是直角三角形的条件有( )A、1个 B、2个 C、3个 D、4个7. 下列各组数据中的三个数,可作为三边长构成直角三角形的是( )A、1、2、3 B、7、8、9 C、6、8、10 D、5、12、208. 如图,在三角形ABC中, , , , , 将三角形沿射线的方向平移个单位长度得到三角形 , 连接 , 则下列结论:①且;②四边形的面积等于四边形DFCG的面积;③四边形的周长为;④其中正确结论的个数为( )
A、 B、 C、 D、4. 下列各组数据为三角形三边,能构成直角三角形的是( )A、 , , B、 , , C、 , , D、 , ,5. △ABC的三条边分别为a,b,c,下列条件不能判断△ABC是直角三角形的是( )A、a2+b2=c2 B、∠A=∠B+∠C C、∠A∶∠B∶∠C=3∶4∶5 D、a=5,b=12,c=136. 在下列条件中:①;②;③;④ , 能确定是直角三角形的条件有( )A、1个 B、2个 C、3个 D、4个7. 下列各组数据中的三个数,可作为三边长构成直角三角形的是( )A、1、2、3 B、7、8、9 C、6、8、10 D、5、12、208. 如图,在三角形ABC中, , , , , 将三角形沿射线的方向平移个单位长度得到三角形 , 连接 , 则下列结论:①且;②四边形的面积等于四边形DFCG的面积;③四边形的周长为;④其中正确结论的个数为( )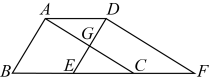 A、1个 B、2个 C、3个 D、4个
A、1个 B、2个 C、3个 D、4个二、填空题
-
9. 如图,∠AOB=30°,点D为∠AOB平分线OC上一点,OD的垂直平分线交OA、OB分别于点P,Q,点E是OA上异于点P的一点,且DE=OP=6,则△ODE的面积为.
 10. 如图,在中, , D为的中点,连结 , 作交于点M.若 , , 则.
10. 如图,在中, , D为的中点,连结 , 作交于点M.若 , , 则.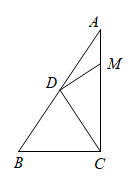 11. 气动升降桌由于高度可调节,给人们学习生活带来许多便捷.如图1所示是桌子的侧平面示意图,AC,BC,DC,DE,HG是固定钢架,HG垂直桌面MN,GE是位置可变的定长钢架.DF是两端固定的伸缩杆,其中,DE=20cm,GE=39cm,GF=13cm,∠EDC是一个固定角为150°,当GE旋转至水平位置时,伸缩杆最短,此时伸缩杆DF的长度为 cm.点D的离地高度为60cm,HG=10cm,小南将桌子调整到他觉得最舒服的高度,此时发现FD=FE,则桌面高度为 cm.
11. 气动升降桌由于高度可调节,给人们学习生活带来许多便捷.如图1所示是桌子的侧平面示意图,AC,BC,DC,DE,HG是固定钢架,HG垂直桌面MN,GE是位置可变的定长钢架.DF是两端固定的伸缩杆,其中,DE=20cm,GE=39cm,GF=13cm,∠EDC是一个固定角为150°,当GE旋转至水平位置时,伸缩杆最短,此时伸缩杆DF的长度为 cm.点D的离地高度为60cm,HG=10cm,小南将桌子调整到他觉得最舒服的高度,此时发现FD=FE,则桌面高度为 cm.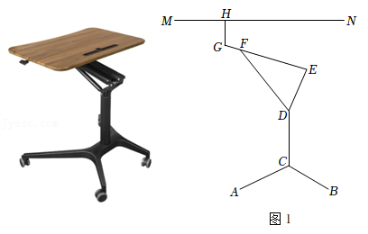 12. 如图,在中, , 于点 , 于点若 , .
12. 如图,在中, , 于点 , 于点若 , . (1)、的长为;(2)、在的腰上取一点 , 当是等腰三角形时,长为.13. 如图,在中, , 为边的中点,、分别为边、上的点,且 , 若 , , 则 , 线段的长度 .
(1)、的长为;(2)、在的腰上取一点 , 当是等腰三角形时,长为.13. 如图,在中, , 为边的中点,、分别为边、上的点,且 , 若 , , 则 , 线段的长度 .
三、解答题
-
14. 如图,在四边形ABCD中,已知∠B=90°,AB=4,BC=3,CD=12,AD=13,求四边形ABCD的面积.
 15. 如图,有两棵树,一棵高6m,另一棵高2m,两树相距5m.一只小鸟从一棵树的树梢飞到另一棵树的树梢,至少飞了多少米?(结果精确到0.1m)
15. 如图,有两棵树,一棵高6m,另一棵高2m,两树相距5m.一只小鸟从一棵树的树梢飞到另一棵树的树梢,至少飞了多少米?(结果精确到0.1m)
四、作图题
-
16. 在直角坐标系中,我们把横坐标、纵坐标均为整数的点称为整点.如图,直线AB分别与x轴、y轴交于点A (-3,0),B(0,4). 请在所给的网格区域(含边界)作图.
 (1)、画一个等腰三角形ABC, 且点C为第一象限内的整点,并写出点C的坐标.(2)、画一个△OAD,使△OAD与△AOB重叠部分的面积是△AOB面积的一半,且点D为整点,并写出点D的坐标.
(1)、画一个等腰三角形ABC, 且点C为第一象限内的整点,并写出点C的坐标.(2)、画一个△OAD,使△OAD与△AOB重叠部分的面积是△AOB面积的一半,且点D为整点,并写出点D的坐标.五、综合题
-
17. 已知线段垂直直线于点 , 点在直线上,分别以 , 为边作等边三角形(点在边的右侧)和等边三角形 , 直线交直线于点 .
 (1)、当点在线段上时,如图1,求证:;(2)、①当点在线段的延长线上时(如图2),请直接写出线段 , , 之间的数量关系;
(1)、当点在线段上时,如图1,求证:;(2)、①当点在线段的延长线上时(如图2),请直接写出线段 , , 之间的数量关系;②当点在线段的延长线上时(如图3),请直接写出线段 , , 之间的数量关系;
③在①和②中,选择其中一个进行证明;
(3)、当 , 且时,请直接写出的长.18. 如图,在直角坐标平面内,已知点、 , 过点A、B分别作x轴的垂线,垂足为点D、E.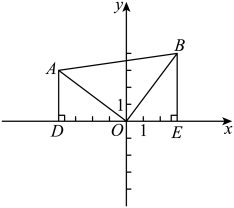 (1)、说明的理由;(2)、求的面积(3)、在x轴上找到点P,使是以为腰的等腰三角形,请直接写出点P的坐标.
(1)、说明的理由;(2)、求的面积(3)、在x轴上找到点P,使是以为腰的等腰三角形,请直接写出点P的坐标.
-