2023-2024学年初中数学八年级上册 19.8 直角三角形全等的性质同步分层训练培优卷(沪教版五四制)

试卷更新日期：2023-07-29 类型：同步测试

进入出卷网下载

一、选择题

1. 如图，等边 $△ A B C$ 中， $B D$ 是 $A C$ 边上的高， $D E ⊥ A B$ 交 $A B$ 于点E，若 $B E = 3$ ，则 $△ A B C$ 的边长为（）

A、3 B、4 C、5 D、无法确定

查看试题解析
2. 如图，等边三角形ABC中，D、E分别为AB、BC边上的两个动点，且总使BD＝CE，AE与CD交于点F，AG⊥CD于点G，则以下结论：（1）△ACE≌△CBD；（2）∠AFG＝60°；（3）AF＝2FG；（4）AC＝2CE.其中正确的结论有（）个

A、4 B、3 C、2 D、1

查看试题解析
3. 如图，Rt△ACB中，∠ACB=90°，∠A=60°，CD、CE分别是△ABC的高和中线，下列说法错误的是（）

A、AD = $\frac{1}{4}$ AB B、S_△CEB= S_△ACE C、AC、BC的垂直平分线都经过E D、图中只有一个等腰三角形

查看试题解析
4. 如图，在 $R t △ A B C$ 中， $∠ A C B = 90 °$ ， $C D ⊥ A B$ 于点D， $∠ 1 = 30 °$ ， $B D = 2$ ，则 $A D$ 的长为（）

A、4 B、6 C、8 D、10

查看试题解析
5. 如图所示，已知 $∠ A O B = 60 °$ ，点P在边OA上， $O P = 8$ ，点M，N在边 $O B$ 上， $P M = P N$ ，若 $M N = 1$ ，则 $O M$ 的长为（）

A、3 B、3.5 C、4 D、4.5

查看试题解析
6. 如图：点 $A (0 ， 2)$ 在 $y$ 轴上， $B$ 是 $x$ 轴上的动点，将线段 $A B$ 绕点 $A$ 逆时针旋转 $60 °$ 得线段 $A C$ ，则 $O C$ 长的最小值为（）

A、 $\frac{\sqrt{3}}{2}$ B、 $1$ C、 $\sqrt{3}$ D、 $2$

查看试题解析
7. 如图，边长为a的等边△ABC中，BF是AC上中线且BF＝b，点D在BF上，连接AD，在AD的右侧作等边△ADE，连接EF，则△AEF周长的最小值是（）

A、 $\frac{1}{2} a + \frac{2}{3} b$ B、 $\frac{1}{2} a + b$ C、a+ $\frac{1}{2}$ b D、 $\frac{3}{2}$ a

查看试题解析
8. 如图，在△ABC中，AB＝AC＝5，BC＝6，D，E分别为线段AB，AC上一点，且AD＝AE，连接BE、CD交于点G，延长AG交BC于点F.以下四个结论正确的是（）
①BF＝CF；②若BE⊥AC，则CF＝DF；③若BE平分∠ABC，则FG＝ $\frac{3}{2}$ ；④连结EF，若BE⊥AC，则∠DFE＝2∠ABE.

A、①②③ B、③④ C、①②④ D、①②③④

查看试题解析

二、填空题

9. 如图，边长为6的等边三角形 $A B C$ 中，若点 $M$ 是高 $A D$ 所在直线上一点，连接 $C M$ ，以 $C M$ 为边在直线 $C M$ 的下方画等边三角形 $C M N$ ，连接 $D N$ ，则 $D N$ 长度的最小值为.

查看试题解析
10. 如图，∠AOP=∠BOP=15°，PC $/ /$ OA，PD⊥OA，若PC=4，则∠COP= ， PD=.

查看试题解析
11. 如图，在 $R t △ A B C$ 中， $∠ A C B = 90 °$ ， $∠ B A C = 30 °$ ， $B C = 5$ ，直线l是 $B C$ 边的垂直平分线，点P是直线l上的一动点，则 $A P + C P$ 的最小值为．

查看试题解析
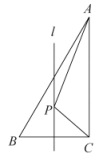12. 如图， $△ A B C$ 是等边三角形，直线 $M N ⊥ A C$ 于点C，点D在直线MN上运动，以AD为边向右作等边 $△ A D E$ ，连接CE，若 $A B = 4$ ，则CE的最小值是．

查看试题解析
13. 如图，点E在等边△ABC的边BC上，BE＝12，射线CD⊥BC于点C，点P是射线CD上一动点，点F是线段AB上一动点，当EP+PF的值最小时，BF＝14，则AC的长为．

查看试题解析

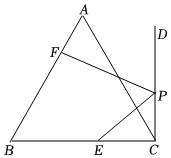
三、解答题

14. 为了推进节能减排，助力实现碳达峰、碳中和，某市新换了一批新能源公交车（如图1）．图2、图3分别是该公交车双开门关闭、打开中某一时刻的俯视（从上面往下看）示意图． $M E$ ， $E F$ ， $F N$ 是门轴的滑动轨道， $∠ E = ∠ F = 90 °$ ，两门 $A B$ ， $C D$ 的门轴 $A$ ， $B$ ， $C$ ， $D$ 都在滑动轨道上，两门关闭时（如图2），点 $A$ ， $D$ 分别在点 $E$ ， $F$ 处，门缝忽略不计（ $B$ ， $C$ 重合），两门同时开启时，点 $A$ ， $D$ 分别沿 $E \to M$ ， $F \to N$ 的方向同时以相同的速度滑动，如图3，当点 $B$ 到达点 $E$ 处时，点 $C$ 恰好到达点 $F$ 处，此时两门完全开启，若 $E F = 1$ 米， $A B = C D$ ，在两门开启的过程中，当 $∠ A B E = 60 °$ 时，求 $B C$ 的长度．

查看试题解析
15. 如图，△ABC中，CD、BE分别是高，M、N分别是线段BC、DE的中点．求证：MN⊥DE.

查看试题解析

四、综合题

16. 如图1，在 $△ A B C$ 中， $C D ， B E$ 分别是 $A B ， A C$ 边上的高线，M，N分别是线段 $B C ， D E$ 的中点.

(1)、求证： $M N ⊥ D E$ .

(2)、连接 $D M ， M E$ ，猜想 $∠ A$ 与 $∠ D M E$ 之间的关系，并说明理由.

(3)、若将锐角三角形 $A B C$ 变为钝角三角形 $A B C$ ，其余条件不变，如图2，直接写出 $∠ B A C$ 与 $∠ D M E$ 之间的关系.

查看试题解析
17. 如图，在等边 $△ A B C$ 中，点D，E分别是 $A C ， A B$ 上的动点，且 $A E = C D$ ， $B D$ 交 $C E$ 于点P.

(1)、如图1，求证： $∠ B P C = 120 °$ ；

(2)、点M是边 $B C$ 的中点，连接 $P A ， P M$ .
①如图2，若点A，P，M三点共线，则 $P A$ 与 $P M$ 的数量关系是 .

②若点A，P，M三点不共线，问①中的结论还成立吗？若成立，请给出证明，若不成立，说明理由.

查看试题解析

2023-2024学年初中数学八年级上册 19.8 直角三角形全等的性质 同步分层训练培优卷(沪教版五四制)

一、选择题

二、填空题

三、解答题

四、综合题

2023-2024学年初中数学八年级上册 19.8 直角三角形全等的性质同步分层训练培优卷(沪教版五四制)