2023-2024学年初中数学八年级上册 19.6 轨迹 同步分层训练培优卷(沪教版五四制)
试卷更新日期:2023-07-29 类型:同步测试
一、选择题
-
1. 已知∠AOB,在射线OA,OB上分别截取OD=OE,分别以点D,E为圆心,以大于 DE且同样长为半径画弧,在∠AOB内两弧交于点C,作射线OC,OC就是∠AOB的角平分线.作图依据是( )A、SAS B、ASA C、SSS D、HL2. 如图,点A在点O的北偏西30°的方向上,AB⊥OA,垂足为A.根据已知条件和图上尺规作图的痕迹判断,下列说法正确的是( )
 A、点O在点A的南偏东60°方向上 B、点B在点A的北偏东30°方向上 C、点B在点O的北偏东60°方向上 D、点B在点O的北偏东30°方向上3. 下列选项中的尺规作图(各图中的点P都在△ABC的边上),能推出PA=PC的是( )A、
A、点O在点A的南偏东60°方向上 B、点B在点A的北偏东30°方向上 C、点B在点O的北偏东60°方向上 D、点B在点O的北偏东30°方向上3. 下列选项中的尺规作图(各图中的点P都在△ABC的边上),能推出PA=PC的是( )A、 B、
B、 C、
C、 D、
D、 4. 如图,在△ABC中,∠C=90°,使点P到AB、BC的距离相等,则符合要求的作图痕迹( )A、
4. 如图,在△ABC中,∠C=90°,使点P到AB、BC的距离相等,则符合要求的作图痕迹( )A、 B、
B、 C、
C、 D、
D、 5. 如图,已知线段AB,以点A,B为圆心,5为半径作弧相交于点C,D.连结CD,点E在CD上,连结CA,CB,EA,EB.若与的周长之差为4,则AE的长为( )
5. 如图,已知线段AB,以点A,B为圆心,5为半径作弧相交于点C,D.连结CD,点E在CD上,连结CA,CB,EA,EB.若与的周长之差为4,则AE的长为( )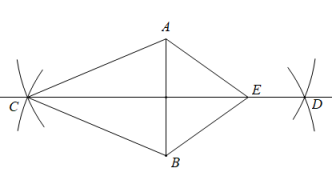 A、1 B、2 C、3 D、46. 如图,在△ABC中,AC=BC>AB,点P为△ABC所在平面内一点,且点P与△ABC的任意两个顶点构成△PAB,△PBC,△PAC均是等腰三角形,则满足上述条件的所有点P的个数为( )
A、1 B、2 C、3 D、46. 如图,在△ABC中,AC=BC>AB,点P为△ABC所在平面内一点,且点P与△ABC的任意两个顶点构成△PAB,△PBC,△PAC均是等腰三角形,则满足上述条件的所有点P的个数为( ) A、3 B、4 C、6 D、77. 如图,在已知的△ABC中,按以下步骤作图:①分别以B、C为圆心,以大于 BC的长为半径作弧,两弧相交于点M、N;②作直线MN交AB于点D , 连接CD , 若CD=AD , ∠B=20°,则下列结论中不正确是( )
A、3 B、4 C、6 D、77. 如图,在已知的△ABC中,按以下步骤作图:①分别以B、C为圆心,以大于 BC的长为半径作弧,两弧相交于点M、N;②作直线MN交AB于点D , 连接CD , 若CD=AD , ∠B=20°,则下列结论中不正确是( )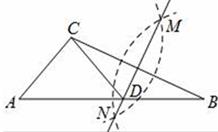 A、∠CAD=40° B、∠ACD=70° C、点D为△ABC的外心 D、∠ACB=90°8. 如图,锐角 中, ,若想找一点P,使得 与 互补,甲、乙、丙三人作法分别如下:
A、∠CAD=40° B、∠ACD=70° C、点D为△ABC的外心 D、∠ACB=90°8. 如图,锐角 中, ,若想找一点P,使得 与 互补,甲、乙、丙三人作法分别如下:甲:以B为圆心,AB长为半径画弧交AC于P点,则P即为所求;
乙:分别以B,C为圆心,AB,AC长为半径画弧交于P点,则P即为所求;
丙:作BC的垂直平分线和 的平分线,两线交于P点,则P即为所求.
对于甲、乙、丙三人的作法,下列叙述正确的是( )
 A、三人皆正确 B、甲、丙正确,乙错误 C、甲正确,乙、丙错误 D、甲错误,乙、丙正确
A、三人皆正确 B、甲、丙正确,乙错误 C、甲正确,乙、丙错误 D、甲错误,乙、丙正确二、填空题
-
9. 如图△ABC中,∠C=90°,以顶点A为圆心,任意长为半径画弧,分别交AC,AB于点M,N,再分别以点M,N为圆心,大于 MN的长为半径画弧,两弧交干点P,作射线AP交边BC于点D,若CD=4,BD=5,AC=12,则△ABD的面积是;
 10. 如图,在△ABC中,∠C=30°,∠B=50°,AD平分∠CAB,那么∠ADC的度数是
10. 如图,在△ABC中,∠C=30°,∠B=50°,AD平分∠CAB,那么∠ADC的度数是 11. 经过定点P,且半径等于2cm的圆的圆心的轨迹 .12. 下面是“求作∠AOB的角平分线”的尺规作图过程.
11. 经过定点P,且半径等于2cm的圆的圆心的轨迹 .12. 下面是“求作∠AOB的角平分线”的尺规作图过程.已知:如图,钝角∠AOB.
求作:∠AOB的角平分线.
作法:
①在OA和OB上,分别截取OD、OE,使OD=OE;
②分别以D、E为圆心,大于 DE的长为半径作弧,在∠AOB内,两弧交于点C;
③作射线OC.
所以射线OC就是所求作的∠AOB的角平分线.
请回答:该尺规作图的依据是 .
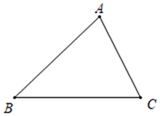
 13. 在等边△ABC所在平面内有点P,且使得△ABP,△ACP,△BCP均为等腰三角形,则符合条件的点P共有个.
13. 在等边△ABC所在平面内有点P,且使得△ABP,△ACP,△BCP均为等腰三角形,则符合条件的点P共有个.三、解答题
-
14. 尺规作图:如图,某地有两个工厂M、N和两条相交叉的公路a,b现计划修建一座物资仓库,希望仓库到两个工厂的距离相等,到两条公路的距离也相等.你能确定仓库应该建在什么位置吗?在所给的图形中画出你的设计方案.(保留作图痕迹).
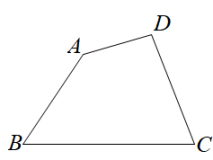
 15. 已知:四边形 .
15. 已知:四边形 .求作:点 , 使 , 且点到边和的距离相等.(写出作图的方法,不必写具体步骤,保留作图痕迹)
四、作图题
-
16. 如图,已知 ,请按步骤用尺规作图并回答下列问题:
第一步:在 和 上分别截取 , ,使 .
第二步:分别以 为圆心,以大于 长为半径作弧,两弧在 内交于点E.
第三步:过点 作射线 .(保留作图痕迹)
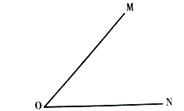 (1)、 与 的关系是什么?请说明理由.(2)、在 上任取一点 ,过点 分别作 于点 , 于点 , 与 相等吗?为什么?
(1)、 与 的关系是什么?请说明理由.(2)、在 上任取一点 ,过点 分别作 于点 , 于点 , 与 相等吗?为什么?五、综合题
-
17. 有三条长度均为a的线段,分别按以下要求画圆.
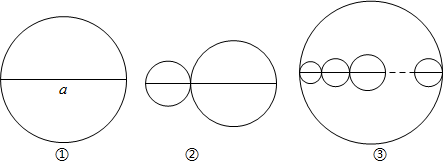 (1)、如图①,以该线段为直径画一个圆,记该圆的周长为C1;如图②,在该线段上任取一点,再分别以两条小线段为直径画两个圆,这两个圆的周长的和为C2 , 请指出C1和C2的数量关系,并说明理由;(2)、如图③,当a=11时,以该线段为直径画一个大圆,再在大圆内画若干小圆,这些小圆的直径都和大圆的直径在同一条直线上,且小圆的直径的和等于大圆的直径,那么图中所有小圆的周长的和为.(直接填写答案,结果保留π)18. 如图,在四边形ABCD中, , 点E在AD上,点F在BC上.
(1)、如图①,以该线段为直径画一个圆,记该圆的周长为C1;如图②,在该线段上任取一点,再分别以两条小线段为直径画两个圆,这两个圆的周长的和为C2 , 请指出C1和C2的数量关系,并说明理由;(2)、如图③,当a=11时,以该线段为直径画一个大圆,再在大圆内画若干小圆,这些小圆的直径都和大圆的直径在同一条直线上,且小圆的直径的和等于大圆的直径,那么图中所有小圆的周长的和为.(直接填写答案,结果保留π)18. 如图,在四边形ABCD中, , 点E在AD上,点F在BC上. (1)、尺规作图:用没有刻度的直尺和圆规,在四边形内部找一点M,使得点M到AD,AB的距离相等,且;(2)、在(1)的条件下,延长AM交BC于点N,且 , 连接EF,求证:E,M,F三点共线.
(1)、尺规作图:用没有刻度的直尺和圆规,在四边形内部找一点M,使得点M到AD,AB的距离相等,且;(2)、在(1)的条件下,延长AM交BC于点N,且 , 连接EF,求证:E,M,F三点共线.
-