2023-2024学年初中数学八年级上册 19.6 轨迹 同步分层训练基础卷(沪教版五四制)
试卷更新日期:2023-07-29 类型:同步测试
一、选择题
-
1. 如图,在中,分别以点A,B为圆心,大于长为半径画弧,两弧相交于点E,F,连接 , 作直线交于点M,连接 , 则下列判断不正确的是( )
 A、 B、 C、 D、2. 如图,在中,分别以 , 为圆心,大于长为半径作弧,两弧分别相交于 , 两点,作直线 , 分别交线段 , 于点 , . 若 , 的周长为 , 则的周长为( )
A、 B、 C、 D、2. 如图,在中,分别以 , 为圆心,大于长为半径作弧,两弧分别相交于 , 两点,作直线 , 分别交线段 , 于点 , . 若 , 的周长为 , 则的周长为( )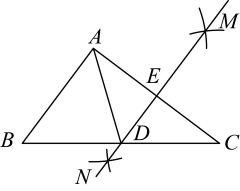 A、 B、 C、 D、3. 如图,用直尺和圆规作出的角平分线 , 在作角平分线过程中,用到的三角形全等的判定方法是( )
A、 B、 C、 D、3. 如图,用直尺和圆规作出的角平分线 , 在作角平分线过程中,用到的三角形全等的判定方法是( )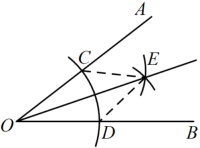 A、 B、 C、 D、4. 如图,在中, . 根据尺规作图痕迹,可得的大小为( )
A、 B、 C、 D、4. 如图,在中, . 根据尺规作图痕迹,可得的大小为( ) A、 B、 C、 D、5. 如图,在中,分别以A,C为圆心,大于长为半径作弧,两弧分别相交于M,N两点,作直线MN,分别交线段BC,AC于点D,E,若的周长为 , 则的周长为( )
A、 B、 C、 D、5. 如图,在中,分别以A,C为圆心,大于长为半径作弧,两弧分别相交于M,N两点,作直线MN,分别交线段BC,AC于点D,E,若的周长为 , 则的周长为( ) A、 B、 C、 D、6. 如图,△ABC中,AB<AC<BC,如果要使用尺规作图的方法在BC上确定一点P,使PA+PB=BC,那么符合要求的作图痕迹是( )A、
A、 B、 C、 D、6. 如图,△ABC中,AB<AC<BC,如果要使用尺规作图的方法在BC上确定一点P,使PA+PB=BC,那么符合要求的作图痕迹是( )A、 B、
B、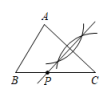 C、
C、 D、
D、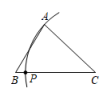 7. 内找一点P,使P到B、C两点的距离相等,并且P到C的距离等于A到C的距离.下列尺规作图正确的是( )A、
7. 内找一点P,使P到B、C两点的距离相等,并且P到C的距离等于A到C的距离.下列尺规作图正确的是( )A、 B、
B、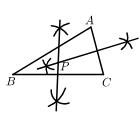 C、
C、 D、
D、 8. 如图是三个基本作图的作图痕迹,关于①,②,③,④四条弧下列说法中错误的是( )
8. 如图是三个基本作图的作图痕迹,关于①,②,③,④四条弧下列说法中错误的是( ) A、弧①是以点O为圆心,以任意长为半径所作的弧 B、弧②是以点B为圆心,以任意长为半径所作的弧 C、弧③是以点A为圆心,以大于的长为半径所作的弧 D、弧④是以点C为圆心,以大于的长为半径所作的弧
A、弧①是以点O为圆心,以任意长为半径所作的弧 B、弧②是以点B为圆心,以任意长为半径所作的弧 C、弧③是以点A为圆心,以大于的长为半径所作的弧 D、弧④是以点C为圆心,以大于的长为半径所作的弧二、填空题
-
9. 到点A的距离等于6cm的点的轨迹是 .10. 如图,在中, , 利用尺规在上分别截取;分别以点M,N为圆心,大于的长为半径作弧,两弧在内部交于点E,作射线交于点F,若 , 点H为线段上的一动点,则的最小值是 .
 11. 如图,将放在每个小正方形边长均为1的网格中,点A、B、C均落在格点上,若点B的坐标为 , 点C的坐标为 , 则到三个顶点距离相等的点的坐标为 .
11. 如图,将放在每个小正方形边长均为1的网格中,点A、B、C均落在格点上,若点B的坐标为 , 点C的坐标为 , 则到三个顶点距离相等的点的坐标为 .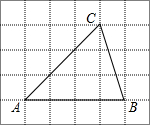 12. 在△中,按以下步骤作图:
12. 在△中,按以下步骤作图:①.分别以为圆心,大于的长为半径画弧相交于两点;②.作直线交于点.连接;若 , 则的度数为 .
 13. 如图所示,在平面直角坐标系中,以O为圆心,适当长为半径画弧,交x轴于点M,交y轴于点N,再分别以点M,N为圆心,大于MN的长为半径画弧,两弧在第二象限交于点P.若点P的坐标为(a,b),则a与b的数量关系为
13. 如图所示,在平面直角坐标系中,以O为圆心,适当长为半径画弧,交x轴于点M,交y轴于点N,再分别以点M,N为圆心,大于MN的长为半径画弧,两弧在第二象限交于点P.若点P的坐标为(a,b),则a与b的数量关系为
三、解答题
-
14. 数学教科书八年级上册告诉我们一种作已知角的平分线的方法.
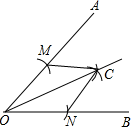
已知:∠AOB.
求作:∠AOB的平分线.
作法:
⑴以点O为圆心,适当长为半径画弧,交OA于点M,交OB于点N.
⑵分别以点M,N为圆心,大于的长为半径画弧,两弧在∠AOB的内部相交于点C.
⑶画射线OC.射线OC即为所求(如图所示).
请你证明:射线OC是∠AOB的平分线.
15. 如图,电信部门要在S区修建一座电视信号发射塔,按照设计要求,发射塔到两个城镇A,B的距离必须相等,到两条高速公路m和n的距离也必须相等,发射塔应修建在什么位置?在图上标出它的位置.(要求用尺规作图,保留作图痕迹,不写作法,要写明结论)
四、作图题
-
16. 如图,在学习了《简单的轴对称图形》一节后,小颖画了一个平角 , 然后利用尺规按照如下步骤作图:
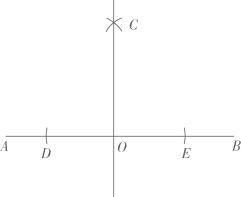
(1)在和上分别截取 , , 使.
(2)分别以 , 为圆心,以大于的长为半径作弧,两弧相交于点.
(3)作直线.于是小颖说直线垂直于.你认为小颖说的对吗?为什么?
五、综合题