2023-2024学年初中数学八年级上册 19.5 角的平分线 同步分层训练培优卷(沪教版五四制)
试卷更新日期:2023-07-29 类型:同步测试
一、选择题
-
1. 如图,点B,A,D在同一条直线上,平分 , 下列不能判定的条件是( )
 A、 B、 C、 D、2. 如图, , 平分 , D是的中点, , 则( )
A、 B、 C、 D、2. 如图, , 平分 , D是的中点, , 则( )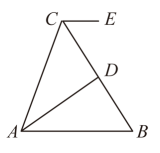 A、 B、 C、 D、3. 在直角三角形ABC中,∠C=90°,AD平分∠BAC交BC于点D,BE平分∠ABC交AC于点E,AD、BE相交于点F,过点D作DG∥AB,过点B作BG⊥DG交DG于点G.下列结论:①∠AFB=135°;②∠BDG=2∠CBE;③BC平分∠ABG;④∠BEC=∠FBG.其中正确的个数是( )
A、 B、 C、 D、3. 在直角三角形ABC中,∠C=90°,AD平分∠BAC交BC于点D,BE平分∠ABC交AC于点E,AD、BE相交于点F,过点D作DG∥AB,过点B作BG⊥DG交DG于点G.下列结论:①∠AFB=135°;②∠BDG=2∠CBE;③BC平分∠ABG;④∠BEC=∠FBG.其中正确的个数是( ) A、1个 B、2个 C、3个 D、4个4. 如图,已知直线和相交于点 , 是直角,平分 , , 则的度数为( )
A、1个 B、2个 C、3个 D、4个4. 如图,已知直线和相交于点 , 是直角,平分 , , 则的度数为( )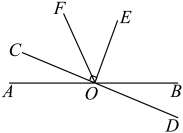 A、 B、 C、 D、72°5. 如图,在△ABC中,AB=AC,AD平分∠BAC,DE⊥AB于E点,DF⊥AC于点F,则下列四个结论:①AD上任意一点到AB,AC两边的距离相等; ②AD⊥BC且BD=CD;③∠BDE=∠CDF;④AE=AF.其中正确的有( )
A、 B、 C、 D、72°5. 如图,在△ABC中,AB=AC,AD平分∠BAC,DE⊥AB于E点,DF⊥AC于点F,则下列四个结论:①AD上任意一点到AB,AC两边的距离相等; ②AD⊥BC且BD=CD;③∠BDE=∠CDF;④AE=AF.其中正确的有( ) A、②③ B、①③ C、①②④ D、①②③④6. 如图,已知△ABC是等边三角形,点D、E分别在边AB、BC上,CD、AE交于点F,∠AFD=60°.FG为△AFC的角平分线,点H在FG的延长线上,HG=CD,连接HA、HC.①BD=CE;②∠AHC=60°;③FC=CG;④S△CBD=S△CGH;其中说法正确的有( )
A、②③ B、①③ C、①②④ D、①②③④6. 如图,已知△ABC是等边三角形,点D、E分别在边AB、BC上,CD、AE交于点F,∠AFD=60°.FG为△AFC的角平分线,点H在FG的延长线上,HG=CD,连接HA、HC.①BD=CE;②∠AHC=60°;③FC=CG;④S△CBD=S△CGH;其中说法正确的有( ) A、1个 B、2个 C、3个 D、4个7. 有一题目:“如图,∠ABC=40°,BD平分∠ABC , 过点D作DE∥AB交BC于点E , 若点F在AB上,且满足DF=DE , 求∠DFB的度数.”小贤的解答:以D为圆心,DE长为半径画圆交AB于点F , 连接DF , 则DE=DF , 由图形的对称性可得∠DFB=∠DEB . 结合平行线的性质可求得∠DFB=140°.而小军说:“小贤考虑的不周全,∠DFB还应有另一个不同的值”.下列判断正确的是( )
A、1个 B、2个 C、3个 D、4个7. 有一题目:“如图,∠ABC=40°,BD平分∠ABC , 过点D作DE∥AB交BC于点E , 若点F在AB上,且满足DF=DE , 求∠DFB的度数.”小贤的解答:以D为圆心,DE长为半径画圆交AB于点F , 连接DF , 则DE=DF , 由图形的对称性可得∠DFB=∠DEB . 结合平行线的性质可求得∠DFB=140°.而小军说:“小贤考虑的不周全,∠DFB还应有另一个不同的值”.下列判断正确的是( ) A、小军说的对,且∠DFB的另一个值是40° B、小军说的不对,∠DFB只有140°一个值 C、小贤求的结果不对,∠DFB应该是20° D、两人都不对,∠DFB应有3个不同值8. 如图,点E是的中点, , , 平分 , 下列结论:①;②;③;④.其中正确的是( )
A、小军说的对,且∠DFB的另一个值是40° B、小军说的不对,∠DFB只有140°一个值 C、小贤求的结果不对,∠DFB应该是20° D、两人都不对,∠DFB应有3个不同值8. 如图,点E是的中点, , , 平分 , 下列结论:①;②;③;④.其中正确的是( ) A、①②④ B、①②③④ C、②③④ D、①③
A、①②④ B、①②③④ C、②③④ D、①③二、填空题
-
9. 如图,在中, , 按以下步骤作图:
①以B为圆心,以任意长为半径作弧,分别交 , 于点M,N;
②分别以M、N为圆心,以大于的长为半径作弧,两弧在内交于点P;
③作射线 , 交于点D.若 , 则点D到直线的距离是 .
 10. 如图,直线 , 的平分线交直线于点D,若 , 则的度数为 .
10. 如图,直线 , 的平分线交直线于点D,若 , 则的度数为 . 11. 如图,在锐角中, , 、为的角平分线.且、交于点 , 连接 . 有下列四个结论:①;②;③;④ . 其中结论正确的序号是 .
11. 如图,在锐角中, , 、为的角平分线.且、交于点 , 连接 . 有下列四个结论:①;②;③;④ . 其中结论正确的序号是 .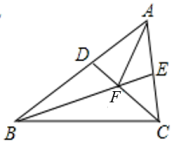 12. 如图,△ABC为等边三角形,点D与点C关于直线AB对称,E,F分别是边BC和AC上的点,BE=CF,AE与BF交于点G.DG交AB于点H.下列四个结论中:①△ABE≌△BCF;②AG+BG=DG;③HG+GE=GF;④△AHF为等边三角形.所有正确结论的序号是 .
12. 如图,△ABC为等边三角形,点D与点C关于直线AB对称,E,F分别是边BC和AC上的点,BE=CF,AE与BF交于点G.DG交AB于点H.下列四个结论中:①△ABE≌△BCF;②AG+BG=DG;③HG+GE=GF;④△AHF为等边三角形.所有正确结论的序号是 . 13. 如图,在中, , , , 是的平分线.若P,Q分别是和上的动点,则的最小值是 .
13. 如图,在中, , , , 是的平分线.若P,Q分别是和上的动点,则的最小值是 .
三、解答题
-
14. 如图,直线 , 相交于点 , 平分 , 已知: . 求和的度数.
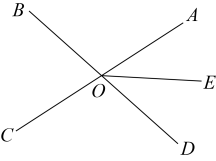 15. 如图,已知 , 平分交的延长线于点E,平分交的延长线于点F,且与交于点G,求证: .
15. 如图,已知 , 平分交的延长线于点E,平分交的延长线于点F,且与交于点G,求证: .
四、作图题
-
16. 如图,点B和点C分别为∠MAN两边上的点,AB=AC.
 (1)、按下列语句画出图形:
(1)、按下列语句画出图形:① AD⊥BC,垂足为D;
② ∠BCN的平分线CE与AD的延长线交于点E
③ 连结BE.
(2)、在完成(1)后不添加线段和字母的情况下,请你写出除△ABD≌△ACD外的两对全等三角形:≌ , ≌;并选择其中的一对全等三角形予以证明.五、综合题
-
17. 已知平分 , 如图1所示,点B在射线上,过点B作于点A,在射线上取一点C,使得 .
 (1)、若线段 , 求线段的长;(2)、如图2,点D是线段上一点,作 , 使得的另一边交于点E,连接 .
(1)、若线段 , 求线段的长;(2)、如图2,点D是线段上一点,作 , 使得的另一边交于点E,连接 .①是否成立,请说明理由;
②请判断三条线段的数量关系,并说明理由.
18. 如图1,在四边形ABCD中, , , 点E在AB边上,DE平分∠ADC.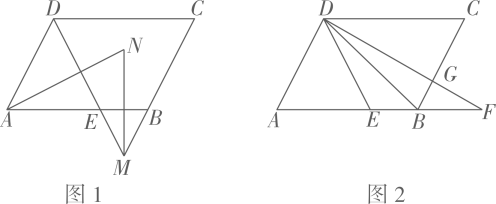 (1)、分别延长DE、CB交于点M,∠DAB与∠CMD的平分线AN、MN交于点N,若∠ADE的度数为56°,求∠N的度数;(2)、如图2,已知DF⊥BC交BC边于点G,交AB边的延长线于点F,且DB平分∠EDF,若∠BDC<45°,试比较∠F与∠EDF的大小,并说明理由.
(1)、分别延长DE、CB交于点M,∠DAB与∠CMD的平分线AN、MN交于点N,若∠ADE的度数为56°,求∠N的度数;(2)、如图2,已知DF⊥BC交BC边于点G,交AB边的延长线于点F,且DB平分∠EDF,若∠BDC<45°,试比较∠F与∠EDF的大小,并说明理由.
-