2023-2024学年初中数学八年级上册 19.4 线段的垂直平分线同步分层训练培优卷(沪教版五四制)

试卷更新日期：2023-07-29 类型：同步测试

进入出卷网下载

一、选择题

1. 如图，△ABC中，D点在AB上，E点在BC上，DE为AB的中垂线．若∠B=∠C，且∠EAC>90°，则根据图中标示的角，下列结论正确的是（）

A、∠1=∠2，∠1<∠3 B、∠1=∠2，∠1>∠3 C、∠l≠∠2，∠1<∠3 D、∠1≠∠2，∠1>∠3

查看试题解析
2. 如图，在△ABC中，AB的垂直平分线分别交BC，AB于D，E两点，若 $A E = 3 c m$ ， △ADC的周长为9 cm，则△ABC的周长是（）

A、6 cm B、12 cm C、15 cm D、24 cm

查看试题解析
3. 已知，如图， $△ A B C$ 中， $A B = A C$ ， $∠ A = 120 °$ ， $B C = 12 c m$ ， $A B$ 的垂直平分线交 $B C$ 于点M，交 $A B$ 于点E， $A C$ 的垂直平分线交 $B C$ 于点N，交 $A C$ 于点F，则 $M N$ 的长为（）

A、3cm B、4cm C、6cm D、12cm

查看试题解析
4. 如图，已知 $△ A B C$ $(A C < B C)$ ，用尺规在 $B C$ 边上确定一点P，使 $P A + P C = B C$ ．下面四种作图中，正确的是（）

A、以B为圆心， $B A$ 为半径画弧，交 $B C$ 于点P，点P为所求 B、以C为圆心， $C A$ 为半径画弧，交 $B C$ 于点P，点P为所求 C、作 $A C$ 的垂直平分线交 $B C$ 于点P，点P为所求 D、作 $A B$ 的垂直平分线交 $B C$ 于点P，点P为所求

查看试题解析
5. 如图，在 $△ A B C$ 中，按以下步骤作图： $①$ 分别以 $B 、 C$ 为圆心，大于 $\frac{1}{2} B C$ 的长为半径作弧，两相交于两点 $M 、 N$ ；②作直线 $M N$ 交 $A B$ 于点 $D$ ，连接 $C D$ .若 $C D = A C ， ∠ A = 50 °$ .则 $∠ A C B$ 的度数为（）

A、 $90 °$ B、 $95 °$ C、 $100 °$ D、 $105 °$

查看试题解析
6. 如图， $B C = 4$ ， $△ B C E$ 的周长为9， $A B$ 的垂直平分线交 $A C$ 于点E，垂足为D，则 $A C =$ （）

A、6 B、5 C、4 D、9

查看试题解析
7. 如图，已知△ABC中高AD恰好平分边BC，∠B=30°，点P是BA延长线上一点，点O是线段AD上一点且OP=OC，下面的结论：①∠APO+∠DCO=30°；②△OPC是等边三角形；③AC=AO+AP；④S_△ABC=S_四_边_形AOCP．其中正确的为（）

A、①②③④ B、①②③ C、②③ D、②③④

查看试题解析
8. 如图，在等腰 $△ A B C$ 中， $A B = A C$ ， $∠ B A C = 120 °$ ， $A D ⊥ B C$ 于点D，点P是 $C A$ 延长线上一点，点O在 $A D$ 延长线上， $O P = O B$ ，下面的结论：① $∠ A P O - ∠ O B D = 30 °$ ；② $△ B P O$ 是正三角形；③ $A B - A P = A O$ ；④ $S_{四边形 A O B P} = 2 S_{△ B O C}$ ，其中正确的个数是（）

A、1个 B、2个 C、3个 D、4个

查看试题解析

二、填空题

9. 如图所示，在边长为2的等边 $△ A B C$ 中，点 $G$ 为 $B C$ 的中点，点 $D$ 为 $A G$ 的中点，过点 $D$ 作 $E F ∥ B C$ 交 $A B$ 于点 $E$ ，交 $A C$ 于点 $F$ ，点 $P$ 是线段 $E F$ 上一个动点，连接 $B P$ ， $G P$ ，则 $△ B P G$ 的周长的最小值是.

查看试题解析
10. 如图，在 $△ A B E$ 中， $A D ⊥ B E$ 于点D，C是 $B E$ 上一点， $B D = D C$ ，且点C在 $A E$ 的垂直平分线上.若 $△ A B C$ 的周长为30，则 $D E$ 的长为.

查看试题解析
11. 如图，已知 $Δ A B C$ 三内角的角平分线交于点D，三边的垂直平分线交于点E，若 $∠ B D C = 130 °$ ，则 $∠ B E C =$ 度．

查看试题解析
12. 如图，在锐角△ABC中，∠ABC＝30°，AC＝3，△ABC的面积为8，P为△ABC内部一点，分别作点P关于AB，BC，AC的对称点P₁ ， P₂ ， P₃ ，连接P₁P₂ ， PP₃ ，则2P₁P₂+PP₃的最小值为．

查看试题解析
13. 如图，将等边△ABC折叠，使得点B恰好落在AC边上的点D处，折痕为EF，O为折痕EF上一动点，若AD=1，AC=3，△OCD周长的最小值是．

查看试题解析

三、解答题

14. 如图，在 $△ A B C$ 中，点D是 $B C$ 的中点，过点D作 $D E ⊥ B C$ 交 $A B$ 于点E，连接 $C E$ ．若 $△ A C E$ 的周长为13， $B C = 5$ ，求 $△ A B C$ 的周长．

查看试题解析

15. 根据以下素材，探索完成任务.

三角形背景下角的关系探索
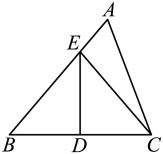
素材1	如图，已知等腰△ABC中，BA＝BC，在腰BC的延长线上取点E，连结AE，作AE的中垂线交射线BC于点D，连结AD.
素材2	研究一个几何问题时，一般先根据几何语言画出几何图形.可能需要分类讨论.
素材3	当我们要论证一个一般性结论时，常常将问题先分成几种特例，在研究特例的过程中寻求规律，总结方法，猜测结论，再将规律、方法和结论迁移到一般情形中，这种数学推理方法叫做归纳法.
问题解决
任务1	补全图形	请根据素材1，把图形补全.你画的点D在点C的 ▲ 侧.
任务2	特例猜想	有下列条件：①AB＝AC；②∠B＝40°；③∠CEA＝20°；④∠CEA＝50°；请从中选择你认为合适的一个或两个条件作为已知条件，求出∠BAD和∠CAE的大小，并猜测∠BAD与∠CAE的数量关系.
任务3	一般结论	请根据你在任务1中所画的一般情况下的图形，写出∠BAD与∠CAE的数量关系，并说明理由.
任务4	拓展延伸	除了你在任务1中所画的情形外，点D相对于点C的位置还有不同的情形吗？若有，请画出图形，并直接写出∠BAD与∠CAE的数量关系.

查看试题解析

四、作图题

16. 下面是小明同学设计的“作一个角等于已知角的2倍”的尺规作图的过程．
已知：如图1， $∠ A O B$ ．
求作： $∠ A D C$ ，使 $∠ A D C = 2 ∠ A O B$ ，且点D在射线 $O A$ 上．
作法：
①如图2，在射线 $O B$ 上任取一点C；
②作线段 $O C$ 的垂直平分线 $M N$ ，交 $O A$ 于点D；
③连接 $D C$ ．
则 $∠ A D C$ 即为所求作的角．
根据上述作图过程，回答问题：

(1)、用直尺和圆规，补全图2中的图形（保留作图痕迹）；

(2)、完成下面的证明：
证明： $∵ M N$ 是线段 $O C$ 的垂直平分线，
$∴ O D =$ ▲ （）（填推理的依据）．
$∴ ∠ A O B = ∠ D C O$ （）（填推理的依据）．
$∵ ∠ A D C = ∠ A O B + ∠ D C O$ ，
$∴ ∠ A D C = 2 ∠ A O B$ ．

查看试题解析

五、综合题

17. 如图，在 $△ ABC$ 中，已知 $AB = AC$ ， $AD$ 是 $BC$ 边上的中线，点 $E$ 是 $AB$ 边上一动点，点 $P$ 是 $AD$ 上的一个动点．

(1)、若 $∠ BAD = 37 °$ ，求 $∠ ACB$ 的度数；

(2)、若 $BC = 6$ ， $AD = 4$ ， $AB = 5$ ，且 $CE ⊥ AB$ 时，求 $CE$ 的长；

(3)、在（2）的条件下，请直接写出 $BP + EP$ 的最小值．

查看试题解析
18. 在 $△ A B C$ 中， $∠ B A C = 110 °$ ， $A C = A B$ ，射线 $A D$ ， $A E$ 的夹角为 $55 °$ ，过点 $B$ 作 $B F ⊥ A D$ 于点 $F$ ，直线 $B F$ 交 $A E$ 于点 $G$ ，连结 $C G$ ．

(1)、如图1，射线 $A D$ ， $A E$ 都在 $∠ B A C$ 的内部．
①设 $∠ B A D = α$ ，则 $∠ C A G =$ （用含有 $α$ 的式子表示）；
②作点 $B$ 关于直线 $A D$ 的对称点 $B^{'}$ ，则线段 $B^{'} G$ 与图1中已有线段的长度相等；

(2)、如图2，射线 $A E$ 在 $∠ B A C$ 的内部，射线 $A D$ 在 $∠ B A C$ 的外部，其他条件不变，用等式表示线段 $B F$ ， $B G$ ， $C G$ 之间的数量关系，并证明．

查看试题解析

2023-2024学年初中数学八年级上册 19.4 线段的垂直平分线 同步分层训练培优卷(沪教版五四制)

一、选择题

二、填空题

三、解答题

四、作图题

五、综合题

2023-2024学年初中数学八年级上册 19.4 线段的垂直平分线同步分层训练培优卷(沪教版五四制)