【备考2024年】中考数学广东卷真题变式分层精准练第4题
试卷更新日期:2023-07-29 类型:二轮复习
一、原题
-
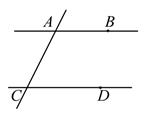
1. 如图,街道与平行,拐角 , 则拐角 ( )
 A、 B、 C、 D、
A、 B、 C、 D、二、基础
-
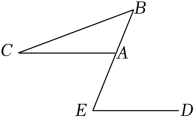
2. 如图,AC∥ED,∠C=26°,∠B=37°,则∠E的大小是( )
 A、53° B、63° C、73° D、833. 如图,直线 , , , 则( )
A、53° B、63° C、73° D、833. 如图,直线 , , , 则( ) A、 B、 C、 D、4. 如图,直线被射线所截, , 若°,则的度数为( )
A、 B、 C、 D、4. 如图,直线被射线所截, , 若°,则的度数为( ) A、 B、 C、 D、5. 将△ABC沿AB方向平移到△EFD的位置,若∠1=31°,∠2=57°,则∠D的度数为( )
A、 B、 C、 D、5. 将△ABC沿AB方向平移到△EFD的位置,若∠1=31°,∠2=57°,则∠D的度数为( ) A、91° B、90° C、92° D、105°6. 如图,直线 , 若 , 则的度数为( )
A、91° B、90° C、92° D、105°6. 如图,直线 , 若 , 则的度数为( ) A、 B、 C、 D、7. 如图,将纸片沿着线段EF剪成两个图形,已知AB∥CD,∠1=75°,则∠2的度数是( )
A、 B、 C、 D、7. 如图,将纸片沿着线段EF剪成两个图形,已知AB∥CD,∠1=75°,则∠2的度数是( ) A、55° B、65° C、75° D、85°8. 如图,直线 , 的平分线交于点 , , 则等于( )
A、55° B、65° C、75° D、85°8. 如图,直线 , 的平分线交于点 , , 则等于( ) A、 B、 C、 D、9. 如图,在平行四边形ABCD中,∠ABC的平分线BE交AD于E,∠AEB=25°,则∠A的大小为( )
A、 B、 C、 D、9. 如图,在平行四边形ABCD中,∠ABC的平分线BE交AD于E,∠AEB=25°,则∠A的大小为( ) A、100° B、120° C、130° D、150°10. 如图,的直角顶点A在直线a上,斜边在直线b上,若 , 则( )
A、100° B、120° C、130° D、150°10. 如图,的直角顶点A在直线a上,斜边在直线b上,若 , 则( ) A、 B、 C、 D、11. 如图,直线 , 则的度数为( )
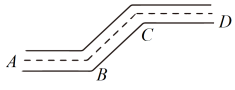
A、 B、 C、 D、11. 如图,直线 , 则的度数为( ) A、 B、 C、 D、12. 如图,工人师傅在工程施工中需在同一平面内弯制一个变形管道ABCD,使AB∥CD,若拐角∠BCD=30°,则∠ABC的度数为( ).
A、 B、 C、 D、12. 如图,工人师傅在工程施工中需在同一平面内弯制一个变形管道ABCD,使AB∥CD,若拐角∠BCD=30°,则∠ABC的度数为( ). A、120° B、130° C、140° D、150°
A、120° B、130° C、140° D、150°三、提高
-
13. 如图,在中,E,F分别是 , 上的点,且 , 是的平分线,分别交 , 于点H,D,则、和之间的数量关系为( )
 A、 B、 C、 D、14. 如图, , BE和DF分别平分∠ABF和∠CDE, , 则∠CDE的度数为( )
A、 B、 C、 D、14. 如图, , BE和DF分别平分∠ABF和∠CDE, , 则∠CDE的度数为( ) A、48° B、32° C、54° D、36°15. 如图,已知直线 , , , 且比大 , 那么的大小是( )
A、48° B、32° C、54° D、36°15. 如图,已知直线 , , , 且比大 , 那么的大小是( )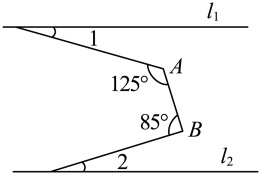 A、 B、 C、 D、16. 公元前200年,古希腊地理学家埃拉托色尼将天文学与测地学结合起来测量地球圆周,他提出设想:在夏至日那天,分别在两地同时观察太阳的位置,并根据地物阴影的长度差异,加以研究分析,从而总结出计算地球圆周的科学方法.他发现,在当时的城市塞恩(图中的A点),直立的杆子在某个时刻没有影子,而此时在500英里以外的亚历山大(图中的B点),直立的杆子的影子却偏离垂直方向(图中角等于).根据这个数据,可以算出地球一周的总长约等于 , 这是因为弧AB的长地球周长的缘故,其中弧AB的长大约为 . 题目中运用到的平行线相关定理是( )
A、 B、 C、 D、16. 公元前200年,古希腊地理学家埃拉托色尼将天文学与测地学结合起来测量地球圆周,他提出设想:在夏至日那天,分别在两地同时观察太阳的位置,并根据地物阴影的长度差异,加以研究分析,从而总结出计算地球圆周的科学方法.他发现,在当时的城市塞恩(图中的A点),直立的杆子在某个时刻没有影子,而此时在500英里以外的亚历山大(图中的B点),直立的杆子的影子却偏离垂直方向(图中角等于).根据这个数据,可以算出地球一周的总长约等于 , 这是因为弧AB的长地球周长的缘故,其中弧AB的长大约为 . 题目中运用到的平行线相关定理是( ) A、对顶角相等 B、两直线平行,同位角相等 C、同旁内角互补,两直线平行 D、两直线平行,内错角相等17. 如图所示的“箭头”图形中,AB∥CD, , 则图中∠G的度数是( )
A、对顶角相等 B、两直线平行,同位角相等 C、同旁内角互补,两直线平行 D、两直线平行,内错角相等17. 如图所示的“箭头”图形中,AB∥CD, , 则图中∠G的度数是( ) A、 B、 C、 D、18. 如图a是长方形纸带,∠DEF=26°,将纸带沿EF折叠成图b,再沿BF折叠成图c,则图c中的∠CFE的度数是( )
A、 B、 C、 D、18. 如图a是长方形纸带,∠DEF=26°,将纸带沿EF折叠成图b,再沿BF折叠成图c,则图c中的∠CFE的度数是( )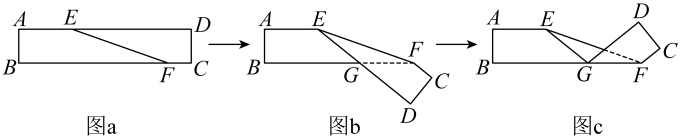 A、102° B、108° C、124° D、128°19. 如图,在中, , 按如图所示进行翻折,使 , , 则的度数是( )
A、102° B、108° C、124° D、128°19. 如图,在中, , 按如图所示进行翻折,使 , , 则的度数是( )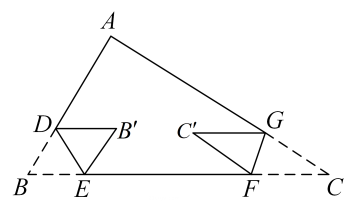 A、 B、 C、 D、20. 已知M,N分别是长方形纸条ABCD边AB,CD上两点(AM>DN),如图1所示,沿M,N所在直线进行第一次折叠,点A,D的对应点分别为点E,F,EM交CD于点P;如图2所示,继续沿PM进行第二次折叠,点B,C的对应点分别为点G,H,若∠1=∠2.则∠CPM的度数为( )
A、 B、 C、 D、20. 已知M,N分别是长方形纸条ABCD边AB,CD上两点(AM>DN),如图1所示,沿M,N所在直线进行第一次折叠,点A,D的对应点分别为点E,F,EM交CD于点P;如图2所示,继续沿PM进行第二次折叠,点B,C的对应点分别为点G,H,若∠1=∠2.则∠CPM的度数为( )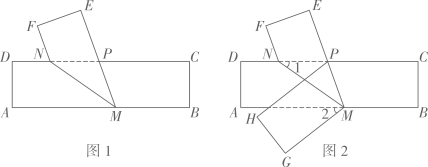 A、74° B、72° C、70° D、68°21. 某同学在一次数学实践活动课中将-条对边互相平行的纸带进行两次折叠(如图) .折痕分别为AB,CD,若CD∥BE,且∠CBE=∠ABC,则∠1为( )
A、74° B、72° C、70° D、68°21. 某同学在一次数学实践活动课中将-条对边互相平行的纸带进行两次折叠(如图) .折痕分别为AB,CD,若CD∥BE,且∠CBE=∠ABC,则∠1为( )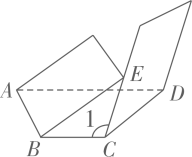 A、106° B、108° C、109° D、110°22. 如图,AB∥EF,∠C=90°,则α、β、γ的关系为( )
A、106° B、108° C、109° D、110°22. 如图,AB∥EF,∠C=90°,则α、β、γ的关系为( )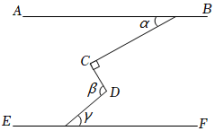 A、α+β-γ=90° B、β=α+γ C、α+β+γ=180° D、β+γ-α=90°
A、α+β-γ=90° B、β=α+γ C、α+β+γ=180° D、β+γ-α=90°四、培优
-
23. 如图, , 为上一点, , 且平分 , 过点作于点 , 且 , 则下列结论:
①;②;③平分;④平分 . 其中正确的是( )
 A、①② B、①②③ C、②③④ D、①②③④24. 如图,长方形纸片ABCD分别沿着EF、DH折叠后,点A,B,C分别落在点A′,B′,C′的位置,当DA'∥B'C'时,∠1=67°,则∠2=( ).
A、①② B、①②③ C、②③④ D、①②③④24. 如图,长方形纸片ABCD分别沿着EF、DH折叠后,点A,B,C分别落在点A′,B′,C′的位置,当DA'∥B'C'时,∠1=67°,则∠2=( ). A、23° B、46° C、56° D、67°25. 如图 , 一副直角三角板和 , 将和按图放置,已知 , 在图的位置上,绕点按逆时针旋转至与重合,在旋转过程中,当与的边平行,旋转的角度是;;;;其中正确的是( )
A、23° B、46° C、56° D、67°25. 如图 , 一副直角三角板和 , 将和按图放置,已知 , 在图的位置上,绕点按逆时针旋转至与重合,在旋转过程中,当与的边平行,旋转的角度是;;;;其中正确的是( )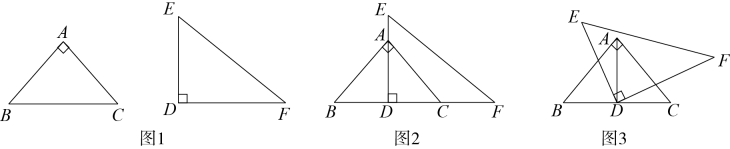 A、 B、 C、 D、26. 如图, , , 平分 , 平分 , 则( )
A、 B、 C、 D、26. 如图, , , 平分 , 平分 , 则( )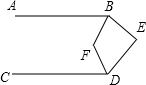 A、 B、 C、 D、27. 如图,已知AB∥CD, , .则 与 之间满足的数量关系是( )
A、 B、 C、 D、27. 如图,已知AB∥CD, , .则 与 之间满足的数量关系是( ) A、 B、 C、 D、28. 如图1,当光线从空气斜入射到某种透明的液体时发生了折射,满足入射角∠1与折射角∠2的度数比为3∶2.如图2,在同一平面上,两条光线同时从空气斜射入这种液体中,两条入射光线与水平液面夹角分别为α,β,在液体中两条折射光线的夹角为γ,则α,β,γ三者之间的数量关系为( )
A、 B、 C、 D、28. 如图1,当光线从空气斜入射到某种透明的液体时发生了折射,满足入射角∠1与折射角∠2的度数比为3∶2.如图2,在同一平面上,两条光线同时从空气斜射入这种液体中,两条入射光线与水平液面夹角分别为α,β,在液体中两条折射光线的夹角为γ,则α,β,γ三者之间的数量关系为( ) A、 (α+β)=γ B、 (α+β)=120°-γ C、α+β=γ D、α+β+γ=180°29. 如图,在平面直角坐标系中,AB∥EG∥x轴,BC∥DE∥HG∥AP∥y轴,点D、C、P、H在x轴上,A(1,2),B(﹣1,2),D(﹣3,0),E(﹣3,﹣2),G(3,﹣2),把一条长为2022个单位长度且没有弹性的细线(细线的粗细忽略不计)的一端固定在点A处,并按A→B→C→D→E→F→G→H→P→A…的规律紧绕在图形“凸”的边上,则细线另一端所在位置的点的坐标是( )
A、 (α+β)=γ B、 (α+β)=120°-γ C、α+β=γ D、α+β+γ=180°29. 如图,在平面直角坐标系中,AB∥EG∥x轴,BC∥DE∥HG∥AP∥y轴,点D、C、P、H在x轴上,A(1,2),B(﹣1,2),D(﹣3,0),E(﹣3,﹣2),G(3,﹣2),把一条长为2022个单位长度且没有弹性的细线(细线的粗细忽略不计)的一端固定在点A处,并按A→B→C→D→E→F→G→H→P→A…的规律紧绕在图形“凸”的边上,则细线另一端所在位置的点的坐标是( ) A、(﹣1,2) B、(﹣1,1) C、(0,1) D、(0,2)30. 如图,已知直线AB,CD被直线AC所截,AB∥CD,E是平面内任意一点 (点E不在直线AB,CD,AC上),设∠BAE=α,∠DCE=β.下列各式:
A、(﹣1,2) B、(﹣1,1) C、(0,1) D、(0,2)30. 如图,已知直线AB,CD被直线AC所截,AB∥CD,E是平面内任意一点 (点E不在直线AB,CD,AC上),设∠BAE=α,∠DCE=β.下列各式:①α+β,②α-β,③β-α,④360°-α-β,
则∠AEC的度数可能是( )
 A、①②③ B、①②④ C、①③④ D、①②③④
A、①②③ B、①②④ C、①③④ D、①②③④
-