广东省历年(2019-2023年)中考数学真题分类汇编6 二次函数
试卷更新日期:2023-07-29 类型:二轮复习
一、选择题
-
1. 如图,抛物线经过正方形的三个顶点A,B,C,点B在轴上,则的值为( )
 A、 B、 C、 D、2. 抛物线 经过点 、 ,且与y轴交于点 ,则当 时,y的值为( )A、-5 B、-3 C、-1 D、53. 我国南宋时期数学家秦九韶曾提出利用三角形的三边求面积的公式,此公式与古希腊几何学家海伦提出的公式如出一辙,即三角形的三边长分别为a , b , c , 记 ,则其面积 .这个公式也被称为海伦-秦九韶公式.若 ,则此三角形面积的最大值为( )A、 B、4 C、 D、54. 二次函数 的图象与一次函数 在同一平面直角坐标系中的图象可能是( )A、
A、 B、 C、 D、2. 抛物线 经过点 、 ,且与y轴交于点 ,则当 时,y的值为( )A、-5 B、-3 C、-1 D、53. 我国南宋时期数学家秦九韶曾提出利用三角形的三边求面积的公式,此公式与古希腊几何学家海伦提出的公式如出一辙,即三角形的三边长分别为a , b , c , 记 ,则其面积 .这个公式也被称为海伦-秦九韶公式.若 ,则此三角形面积的最大值为( )A、 B、4 C、 D、54. 二次函数 的图象与一次函数 在同一平面直角坐标系中的图象可能是( )A、 B、
B、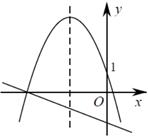 C、
C、 D、
D、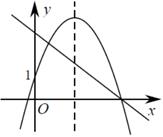 5. 二次函数y=ax2+bx+c(a≠0)的顶点坐标为(-1,n),其部分图象如图所示,以下结论错误的是( )
5. 二次函数y=ax2+bx+c(a≠0)的顶点坐标为(-1,n),其部分图象如图所示,以下结论错误的是( )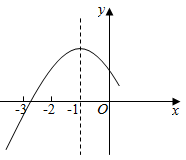 A、
A、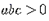 B、4ac-b2<0
C、3a+c>0
D、ax2+bx+c=n+1无实数根
6. 如图,抛物线 的对称轴是 .下列结论:① ;② ;③ ;④ ,正确的有( )
B、4ac-b2<0
C、3a+c>0
D、ax2+bx+c=n+1无实数根
6. 如图,抛物线 的对称轴是 .下列结论:① ;② ;③ ;④ ,正确的有( )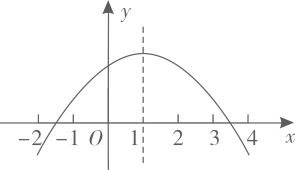 A、4个 B、3个 C、2个 D、1个7. 已知y=ax2+bx+c(a≠0)的图象如图,则y=ax+b和y= 的图象为( )
A、4个 B、3个 C、2个 D、1个7. 已知y=ax2+bx+c(a≠0)的图象如图,则y=ax+b和y= 的图象为( )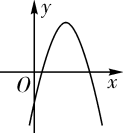 A、
A、 B、
B、 C、
C、 D、
D、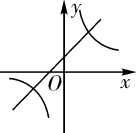
二、填空题
-
8. 把抛物线 向左平移1个单位长度,再向下平移3个单位长度,得到的抛物线的解析式为 .9. 对某条线段的长度进行了3次测量,得到3个结果(单位: )9.9,10.1,10.0,若用 作为这条线段长度的近以值,当 mm 时, 最小.对另一条线段的长度进行了 次测量,得到 个结果(单位: ) ,若用 作为这条线段长度的近似值,当 时, 最小.
三、综合题
-
10. 蔬菜大棚是一种具有出色的保温性能的框架覆膜结构,它的出现使得人们可以吃到反季节蔬菜.一般蔬菜大棚使用竹结构或者钢结构的骨架,上面覆上一层或多层保温塑料膜,这样就形成了一个温室空间.如图,某个温室大棚的横截面可以看作矩形ABCD和抛物线AED构成,其中AB=3m,BC=4m,取BC中点O,过点O作线段BC的垂直平分线OE交抛物线AED于点E,若以O点为原点,BC所在直线为x轴,OE为y轴建立如图所示平面直角坐标系.
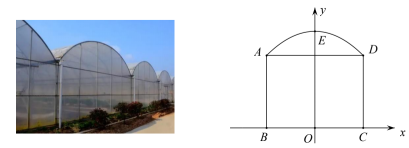
请回答下列问题:
(1)、如图,抛物线的顶点 , 求抛物线的解析式;(2)、如图,为了保证蔬菜大棚的通风性,该大棚要安装两个正方形孔的排气装置 , , 若 , 求两个正方形装置的间距的长;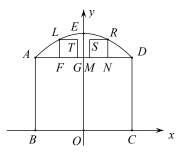 (3)、如图,在某一时刻,太阳光线透过A点恰好照射到C点,此时大棚截面的阴影为 , 求的长.
(3)、如图,在某一时刻,太阳光线透过A点恰好照射到C点,此时大棚截面的阴影为 , 求的长. 11. 端午节是我国入选世界非物质文化遗产的传统节日,端午节吃粽子是中华民族的传统习俗.市场上豆沙粽的进价比猪肉粽的进价每盒便宜10元,某商家用8000元购进的猪肉粽和用6000元购进的豆沙粽盒数相同.在销售中,该商家发现猪肉粽每盒售价50元时,每天可售出100盒;每盒售价提高1元时,每天少售出2盒.(1)、求猪肉粽和豆沙粽每盒的进价;(2)、设猪肉粽每盒售价x元 表示该商家每天销售猪肉粽的利润(单位:元),求y关于x的函数解析式并求最大利润.12. 某科技公司销售高新科技产品,该产品成本为8万元,销售单价x(万元)与销售量y(件)的关系如下表所示:
11. 端午节是我国入选世界非物质文化遗产的传统节日,端午节吃粽子是中华民族的传统习俗.市场上豆沙粽的进价比猪肉粽的进价每盒便宜10元,某商家用8000元购进的猪肉粽和用6000元购进的豆沙粽盒数相同.在销售中,该商家发现猪肉粽每盒售价50元时,每天可售出100盒;每盒售价提高1元时,每天少售出2盒.(1)、求猪肉粽和豆沙粽每盒的进价;(2)、设猪肉粽每盒售价x元 表示该商家每天销售猪肉粽的利润(单位:元),求y关于x的函数解析式并求最大利润.12. 某科技公司销售高新科技产品,该产品成本为8万元,销售单价x(万元)与销售量y(件)的关系如下表所示:x(万元)
10
12
14
16
y(件)
40
30
20
10
(1)、求y与x的函数关系式;(2)、当销售单价为多少时,有最大利润,最大利润为多少?13. 平面直角坐标系 中,抛物线 过点 , , ,顶点 不在第一象限,线段 上有一点 ,设 的面积为 , 的面积为 , .(1)、用含 的式子表示 ;(2)、求点 的坐标;(3)、若直线 与抛物线 的另一个交点 的横坐标为 ,求 在 时的取值范围(用含 的式子表示).14. 如图,平面直角坐标系 中, 的边 在 轴上,对角线 , 交于点 ,函数 的图象经过点 和点 .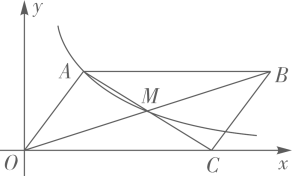 (1)、求 的值和点 的坐标;(2)、求 的周长.15. 如图,抛物线 与 轴交于 , 两点,点 , 分别位于原点的左、右两侧, ,过点 的直线与 轴正半轴和抛物线的交点分别为 , , .
(1)、求 的值和点 的坐标;(2)、求 的周长.15. 如图,抛物线 与 轴交于 , 两点,点 , 分别位于原点的左、右两侧, ,过点 的直线与 轴正半轴和抛物线的交点分别为 , , . (1)、求 , 的值;(2)、求直线 的函数解析式;(3)、点 在抛物线的对称轴上且在 轴下方,点 在射线 上,当 与 相似时,请直接写出所有满足条件的点 的坐标.16. 随着粤港澳大湾区建设的加速推进,广东省正加速布局以5G等为代表的战略性新兴产业,据统计,目前广东5G基站的数量约1.5万座,计划到2020年底,全省5G基站数是目前的4倍,到2022年底,全省5G基站数量将达到17.34万座。(1)、计划到2020年底,全省5G基站的数量是多少万座?;(2)、按照计划,求2020年底到2022年底,全省5G基站数量的年平均增长率。17. 已知抛物线(1)、当 时,请判断点(2,4)是否在该抛物线上;(2)、该抛物线的顶点随着m的变化而移动,当顶点移动到最高处时,求该抛物线的顶点坐标;(3)、已知点 、 ,若该抛物线与线段EF只有一个交点,求该抛物线顶点横坐标的取值范围.18. 已知二次函数 的图象过点 ,且对任意实数x , 都有 .(1)、求该二次函数的解析式;(2)、若(1)中二次函数图象与x轴的正半轴交点为A , 与y轴交点为C;点M是(1)中二次函数图象上的动点.问在x轴上是否存在点N , 使得以A、C、M、N为顶点的四边形是平行四边形.若存在,求出所有满足条件的点N的坐标;若不存在,请说明理由.19. 如图1,抛物线y=ax2+bx+3(a≠0)与x轴交于A(-3,0)和B(1,0),与y轴交于点C,顶点为D.
(1)、求 , 的值;(2)、求直线 的函数解析式;(3)、点 在抛物线的对称轴上且在 轴下方,点 在射线 上,当 与 相似时,请直接写出所有满足条件的点 的坐标.16. 随着粤港澳大湾区建设的加速推进,广东省正加速布局以5G等为代表的战略性新兴产业,据统计,目前广东5G基站的数量约1.5万座,计划到2020年底,全省5G基站数是目前的4倍,到2022年底,全省5G基站数量将达到17.34万座。(1)、计划到2020年底,全省5G基站的数量是多少万座?;(2)、按照计划,求2020年底到2022年底,全省5G基站数量的年平均增长率。17. 已知抛物线(1)、当 时,请判断点(2,4)是否在该抛物线上;(2)、该抛物线的顶点随着m的变化而移动,当顶点移动到最高处时,求该抛物线的顶点坐标;(3)、已知点 、 ,若该抛物线与线段EF只有一个交点,求该抛物线顶点横坐标的取值范围.18. 已知二次函数 的图象过点 ,且对任意实数x , 都有 .(1)、求该二次函数的解析式;(2)、若(1)中二次函数图象与x轴的正半轴交点为A , 与y轴交点为C;点M是(1)中二次函数图象上的动点.问在x轴上是否存在点N , 使得以A、C、M、N为顶点的四边形是平行四边形.若存在,求出所有满足条件的点N的坐标;若不存在,请说明理由.19. 如图1,抛物线y=ax2+bx+3(a≠0)与x轴交于A(-3,0)和B(1,0),与y轴交于点C,顶点为D.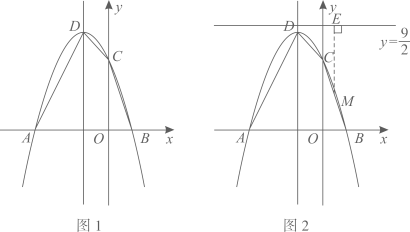 (1)、求解抛物线解析式;(2)、连接AD,CD,BC,将△OBC沿着x轴以每秒1个单位长度的速度向左平移,得到 ,点O、B、C的对应点分别为点 , , ,设平移时间为t秒,当点O'与点A重合时停止移动.记 与四边形AOCD的重叠部分的面积为S,请直接写出S与时间t的函数解析式;(3)、如图2,过抛物线上任意一点M(m,n)向直线l: 作垂线,垂足为E,试问在该抛物线的对称轴上是否存在一点F,使得ME-MF= ?若存在,请求F点的坐标;若不存在,请说明理由.20. 如图抛物线经y=ax2+bx+c过点A(-1,0),点C(0,3),且OB=OC.
(1)、求解抛物线解析式;(2)、连接AD,CD,BC,将△OBC沿着x轴以每秒1个单位长度的速度向左平移,得到 ,点O、B、C的对应点分别为点 , , ,设平移时间为t秒,当点O'与点A重合时停止移动.记 与四边形AOCD的重叠部分的面积为S,请直接写出S与时间t的函数解析式;(3)、如图2,过抛物线上任意一点M(m,n)向直线l: 作垂线,垂足为E,试问在该抛物线的对称轴上是否存在一点F,使得ME-MF= ?若存在,请求F点的坐标;若不存在,请说明理由.20. 如图抛物线经y=ax2+bx+c过点A(-1,0),点C(0,3),且OB=OC. (1)、求抛物线的解析式及其对称轴;(2)、点D、E在直线x=1上的两个动点,且DE=1,点D在点E的上方,求四边形ACDE的周长的最小值;(3)、点P为抛物线上一点,连接CP,直线CP把四边形APBC面积分为3:5两部分,求点P的坐标.21. 如图1,在平面直角坐标系中,抛物线 与 轴交于点 、 (点 在点 右侧),点 为抛物线的顶点.点 在 轴的正半轴上, 交 轴于点 , 绕点 顺时针旋转得到 ,点 恰好旋转到点 ,连接 .
(1)、求抛物线的解析式及其对称轴;(2)、点D、E在直线x=1上的两个动点,且DE=1,点D在点E的上方,求四边形ACDE的周长的最小值;(3)、点P为抛物线上一点,连接CP,直线CP把四边形APBC面积分为3:5两部分,求点P的坐标.21. 如图1,在平面直角坐标系中,抛物线 与 轴交于点 、 (点 在点 右侧),点 为抛物线的顶点.点 在 轴的正半轴上, 交 轴于点 , 绕点 顺时针旋转得到 ,点 恰好旋转到点 ,连接 .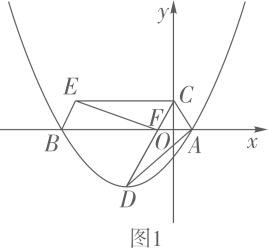
 (1)、求点 、 、 的坐标;(2)、求证:四边形 是平行四边形;(3)、如图2,过顶点 作 轴于点 ,点 是抛物线上一动点,过点 作 轴,点 为垂足,使得 与 相似(不含全等).
(1)、求点 、 、 的坐标;(2)、求证:四边形 是平行四边形;(3)、如图2,过顶点 作 轴于点 ,点 是抛物线上一动点,过点 作 轴,点 为垂足,使得 与 相似(不含全等).①求出一个满足以上条件的点 的横坐标;
②直接回答这样的点 共有几个?
22. 已知抛物线G: 有最低点。(1)、求二次函数 的最小值(用含m的式子表示);(2)、将抛物线G向右平移m个单位得到抛物线G1。经过探究发现,随着m的变化,抛物线G1顶点的纵坐标y与横坐标x之间存在一个函数关系,求这个函数关系式,并写出自变量x的取值范围;(3)、记(2)所求的函数为H,抛物线G与函数H的图像交于点P,结合图像,求点P的纵坐标的取值范围.