广东省历年(2019-2023年)中考数学真题分类汇编5 一次函数与反比例函数
试卷更新日期:2023-07-29 类型:二轮复习
一、选择题
-
1. 如图1,在中,动点P从A点运动到B点再到C点后停止,速度为2单位/s,其中长与运动时间t(单位:s)的关系如图2,则的长为( )
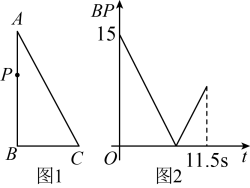 A、 B、 C、17 D、2. 一次函数 的图象过点 , , ,则( )A、 B、 C、 D、3. 若点 , , 在反比例函数 的图像上,则 的大小关系是( )A、 B、 C、 D、4. 在平面直角坐标系xOy中,矩形OABC的点A在函数 的图象上,点C在函数 的图象上,若点B的横坐标为 ,则点A的坐标为( )A、 B、 C、 D、
A、 B、 C、17 D、2. 一次函数 的图象过点 , , ,则( )A、 B、 C、 D、3. 若点 , , 在反比例函数 的图像上,则 的大小关系是( )A、 B、 C、 D、4. 在平面直角坐标系xOy中,矩形OABC的点A在函数 的图象上,点C在函数 的图象上,若点B的横坐标为 ,则点A的坐标为( )A、 B、 C、 D、二、填空题
-
5. 如图,与位于平面直角坐标系中, , , , 若 , 反比例函数恰好经过点C,则 .
 6. 某蓄电池的电压为 , 使用此蓄电池时,电流(单位:)与电阻(单位:)的函数表达式为 , 当时,的值为 .7. 一元二次方程 有两个相等的实数根,点 、 是反比例函数 上的两个点,若 ,则 (填“<”或“>”或“=”).8. 如图,已知反比例函数过A , B两点,A点坐标 ,直线 经过原点,将线段 绕点B顺时针旋转90°得到线段 ,则C点坐标为 .
6. 某蓄电池的电压为 , 使用此蓄电池时,电流(单位:)与电阻(单位:)的函数表达式为 , 当时,的值为 .7. 一元二次方程 有两个相等的实数根,点 、 是反比例函数 上的两个点,若 ,则 (填“<”或“>”或“=”).8. 如图,已知反比例函数过A , B两点,A点坐标 ,直线 经过原点,将线段 绕点B顺时针旋转90°得到线段 ,则C点坐标为 .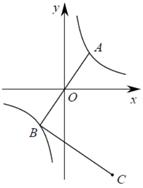 9. 如图,在平面直角坐标系中,ABCO为平行四边形,O(0,0),A(3,1),B(1,2),反比例函数 的图象经过▱OABC的顶点C,则k= .
9. 如图,在平面直角坐标系中,ABCO为平行四边形,O(0,0),A(3,1),B(1,2),反比例函数 的图象经过▱OABC的顶点C,则k= . 10. 如图,在平面直角坐标系中,A(0,-3),∠ABC=90°,y轴平分∠BAC,AD=3CD,若点C在反比例函数y= 上,则k= .
10. 如图,在平面直角坐标系中,A(0,-3),∠ABC=90°,y轴平分∠BAC,AD=3CD,若点C在反比例函数y= 上,则k= .
三、计算题
-
11.(1)、计算:;(2)、已知一次函数的图象经过点与点 , 求该一次函数的表达式.
四、解答题
-
12. 已知反比例函数 的图象分别位于第二、第四象限,化简: .
五、综合题
-
13. 某科技公司销售高新科技产品,该产品成本为8万元,销售单价x(万元)与销售量y(件)的关系如下表所示:
x(万元)
10
12
14
16
y(件)
40
30
20
10
(1)、求y与x的函数关系式;(2)、当销售单价为多少时,有最大利润,最大利润为多少?14. 粤港澳大湾区自动驾驶产业联盟积极推进自动驾驶出租车应用落地工作,无人化是自动驾驶的终极目标.某公交集团拟在今明两年共投资9000万元改装260辆无人驾驶出租车投放市场.今年每辆无人驾驶出租车的改装费用是50万元,预计明年每辆无人驾驶出租车的改装费用可下降 .(1)、求明年每辆无人驾驶出租车的预计改装费用是多少万元;(2)、求明年改装的无人驾驶出租车是多少辆.15. 如图,平面直角坐标系 中, 的边 在 轴上,对角线 , 交于点 ,函数 的图象经过点 和点 .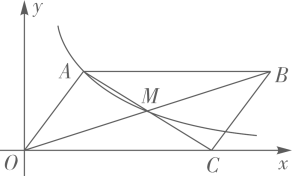 (1)、求 的值和点 的坐标;(2)、求 的周长.16. 有A,B两个发电厂,每焚烧一吨垃圾,A发电厂比B发电厂多发40度电,A焚烧20吨垃圾比B焚烧30吨垃圾少1800度电.(1)、求焚烧1吨垃圾,A和B各发电多少?(2)、A,B两个发电厂共焚烧90吨的垃圾,A焚烧的垃圾不多于B焚烧的垃圾两倍,求A厂和B厂总发电量最大为多少度?17. 已知(1)、化简P;(2)、若点(a , b)在一次函数 的图像上,求P的值。18. 如图,在平面直角坐标系xOy中,菱形ABCD的对角线AC与BD交于点P(-1,2),AB⊥x轴于点E,正比例函数y=mx的图像与反比例函数 的图像相交于A,P两点。
(1)、求 的值和点 的坐标;(2)、求 的周长.16. 有A,B两个发电厂,每焚烧一吨垃圾,A发电厂比B发电厂多发40度电,A焚烧20吨垃圾比B焚烧30吨垃圾少1800度电.(1)、求焚烧1吨垃圾,A和B各发电多少?(2)、A,B两个发电厂共焚烧90吨的垃圾,A焚烧的垃圾不多于B焚烧的垃圾两倍,求A厂和B厂总发电量最大为多少度?17. 已知(1)、化简P;(2)、若点(a , b)在一次函数 的图像上,求P的值。18. 如图,在平面直角坐标系xOy中,菱形ABCD的对角线AC与BD交于点P(-1,2),AB⊥x轴于点E,正比例函数y=mx的图像与反比例函数 的图像相交于A,P两点。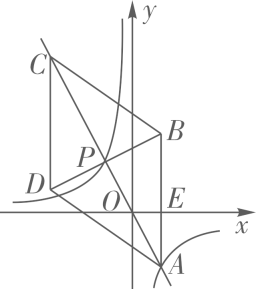 (1)、求m,n的值与点A的坐标;(2)、求证: ∽(3)、求 的值19. 综合运用
(1)、求m,n的值与点A的坐标;(2)、求证: ∽(3)、求 的值19. 综合运用如图1,在平面直角坐标系中,正方形的顶点A在轴的正半轴上,如图2,将正方形绕点逆时针旋转,旋转角为 , 交直线于点 , 交轴于点 .
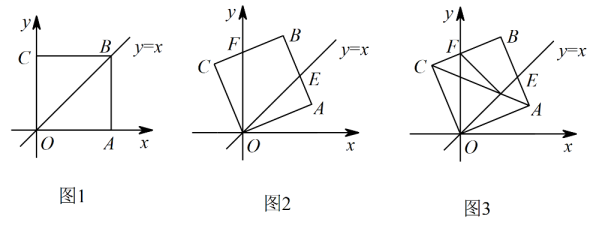 (1)、当旋转角为多少度时,;(直接写出结果,不要求写解答过程)(2)、若点 , 求的长;(3)、如图3,对角线交轴于点 , 交直线于点 , 连接 , 将与的面积分别记为与 , 设 , , 求关于的函数表达式.20. 已知抛物线(1)、当 时,请判断点(2,4)是否在该抛物线上;(2)、该抛物线的顶点随着m的变化而移动,当顶点移动到最高处时,求该抛物线的顶点坐标;(3)、已知点 、 ,若该抛物线与线段EF只有一个交点,求该抛物线顶点横坐标的取值范围.21. 在平面直角坐标系 中,一次函数 的图象与x轴、y轴分别交于A、B两点,且与反比例函数 图象的一个交点为 .(1)、求m的值;(2)、若 ,求k的值.22. 探究:是否存在一个新矩形,使其周长和面积为原矩形的2倍、 倍、k倍.(1)、若该矩形为正方形,是否存在一个正方形,使其周长和面积都为边长为2的正方形的2倍?(填“存在”或“不存在”).(2)、继续探究,是否存在一个矩形,使其周长和面积都为长为3,宽为2的矩形的2倍?
(1)、当旋转角为多少度时,;(直接写出结果,不要求写解答过程)(2)、若点 , 求的长;(3)、如图3,对角线交轴于点 , 交直线于点 , 连接 , 将与的面积分别记为与 , 设 , , 求关于的函数表达式.20. 已知抛物线(1)、当 时,请判断点(2,4)是否在该抛物线上;(2)、该抛物线的顶点随着m的变化而移动,当顶点移动到最高处时,求该抛物线的顶点坐标;(3)、已知点 、 ,若该抛物线与线段EF只有一个交点,求该抛物线顶点横坐标的取值范围.21. 在平面直角坐标系 中,一次函数 的图象与x轴、y轴分别交于A、B两点,且与反比例函数 图象的一个交点为 .(1)、求m的值;(2)、若 ,求k的值.22. 探究:是否存在一个新矩形,使其周长和面积为原矩形的2倍、 倍、k倍.(1)、若该矩形为正方形,是否存在一个正方形,使其周长和面积都为边长为2的正方形的2倍?(填“存在”或“不存在”).(2)、继续探究,是否存在一个矩形,使其周长和面积都为长为3,宽为2的矩形的2倍?同学们有以下思路:
①设新矩形长和宽为x、y , 则依题意 , ,
联立 得 ,再探究根的情况:
根据此方法,请你探究是否存在一个矩形,使其周长和面积都为原矩形的 倍;
②如图也可用反比例函数与一次函数证明 : , : ,那么,
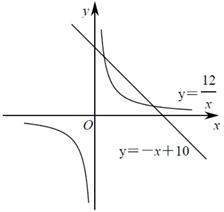
a . 是否存在一个新矩形为原矩形周长和面积的2倍?
b . 请探究是否有一新矩形周长和面积为原矩形的 ,若存在,用图像表达;
c . 请直接写出当结论成立时k的取值范围:.
23. 端午节前夕,某商铺用620元购进50个肉粽和30个蜜枣粽,肉粽的进货单价比蜜枣粽的进货单价多6元.(1)、肉粽和蜜枣粽的进货单价分别是多少元?(2)、由于粽子畅销,商铺决定再购进这两种粽子共300个,其中肉粽数量不多于蜜枣粽数量的2倍,且每种粽子的进货单价保持不变,若肉粽的销售单价为14元,蜜枣粽的销售单价为6元,试问第二批购进肉粽多少个时,全部售完后,第二批粽子获得利润最大?第二批粽子的最大利润是多少元?24. 如图,点 是反比例函数 ( )图象上一点,过点 分别向坐标轴作垂线,垂足为 , ,反比例函数 ( )的图象经过 的中点 ,与 , 分别相交于点 , .连接 并延长交 轴于点 ,点 与点 关于点 对称,连接 , .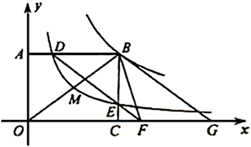 (1)、填空: ;(2)、求 的面积;(3)、求证:四边形 为平行四边形.25. 已知在平面直角坐标系中,点A(3,0),B(-3,0),C(-3,8),以线段BC为直径作圆,圆心为E,直线AC交□E于点D,连接OD.
(1)、填空: ;(2)、求 的面积;(3)、求证:四边形 为平行四边形.25. 已知在平面直角坐标系中,点A(3,0),B(-3,0),C(-3,8),以线段BC为直径作圆,圆心为E,直线AC交□E于点D,连接OD.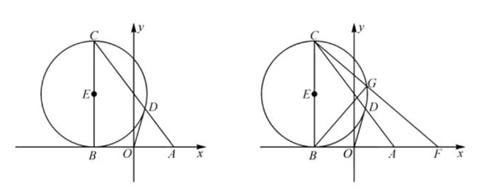 (1)、求证:直线OD是□E的切线;(2)、点F为x轴上任意一点,连接CF交□E于点G,连接BG:
(1)、求证:直线OD是□E的切线;(2)、点F为x轴上任意一点,连接CF交□E于点G,连接BG:当tan∠FCA= ,求所有F点的坐标(直接写出);
-
-