广东省历年(2019-2023年)中考数学真题分类汇编4 方程与不等式
试卷更新日期:2023-07-29 类型:二轮复习
一、选择题
-
1. 不等式 的解集在数轴上表示为( )A、
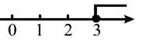 B、
B、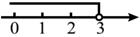 C、
C、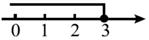 D、
D、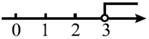 2. 一元一次不等式组的解集为 ( )A、 B、 C、 D、3. 不等式组 的解集为( )A、无解 B、 C、 D、4. 若 ,则 ( )A、 B、 C、 D、95. 《九章算术》中有问题:1亩好田是300元,7亩坏田是500元,一人买了好田坏田一共是100亩,花费了10000元,问他买了多少亩好田和坏田?设一亩好田为x元,一亩坏田为y元,根据题意列方程组得( )A、 B、 C、 D、6. 下面命题正确的是( )A、矩形对角线互相垂直 B、方程x2=14x的解为x=14 C、六边形内角和为540° D、一条斜边和一条直角边分别相等的两个直角三角形全等7. 关于x的一元二次方程 有两个实数根 , ,则k的值( )A、0或2 B、-2或2 C、-2 D、28. 已知 、 是一元二次方程 的两个实数根,下列结论错误的是( )A、 B、 C、 D、9. 某运输公司运输一批货物,已知大货车比小货车每辆多运输5吨货物,且大货车运输75吨货物所用车辆数与小货车运输50吨货物所用车辆数相同,设有大货车每辆运输x吨,则所列方程正确的是( ).A、 B、 C、 D、10. 方程 的解为( )A、 B、 C、 D、11. 以下说法正确的是( )A、平行四边形的对边相等 B、圆周角等于圆心角的一半 C、分式方程 的解为x=2 D、三角形的一个外角等于两个内角的和12. 甲、乙二人做某种机械零件,已知每小时甲比乙少做8个,甲做120个所用的时间与乙做150个所用的时间相等,设甲每小时做x个零件,下列方程正确的是( )A、 B、 C、 D、
2. 一元一次不等式组的解集为 ( )A、 B、 C、 D、3. 不等式组 的解集为( )A、无解 B、 C、 D、4. 若 ,则 ( )A、 B、 C、 D、95. 《九章算术》中有问题:1亩好田是300元,7亩坏田是500元,一人买了好田坏田一共是100亩,花费了10000元,问他买了多少亩好田和坏田?设一亩好田为x元,一亩坏田为y元,根据题意列方程组得( )A、 B、 C、 D、6. 下面命题正确的是( )A、矩形对角线互相垂直 B、方程x2=14x的解为x=14 C、六边形内角和为540° D、一条斜边和一条直角边分别相等的两个直角三角形全等7. 关于x的一元二次方程 有两个实数根 , ,则k的值( )A、0或2 B、-2或2 C、-2 D、28. 已知 、 是一元二次方程 的两个实数根,下列结论错误的是( )A、 B、 C、 D、9. 某运输公司运输一批货物,已知大货车比小货车每辆多运输5吨货物,且大货车运输75吨货物所用车辆数与小货车运输50吨货物所用车辆数相同,设有大货车每辆运输x吨,则所列方程正确的是( ).A、 B、 C、 D、10. 方程 的解为( )A、 B、 C、 D、11. 以下说法正确的是( )A、平行四边形的对边相等 B、圆周角等于圆心角的一半 C、分式方程 的解为x=2 D、三角形的一个外角等于两个内角的和12. 甲、乙二人做某种机械零件,已知每小时甲比乙少做8个,甲做120个所用的时间与乙做150个所用的时间相等,设甲每小时做x个零件,下列方程正确的是( )A、 B、 C、 D、二、填空题
-
13. 已知方程 的一个根是1,则m的值为 .14. 某商品进价4元,标价5元出售,商家准备打折销售,但其利润率不能少于10%,则最多可打折.15. 一元二次方程 有两个相等的实数根,点 、 是反比例函数 上的两个点,若 ,则 (填“<”或“>”或“=”).16. 二元一次方程组 的解为 .17. 若一元二次方程 (b , c为常数)的两根 满足 ,则符合条件的一个方程为 .18. 方程 的解是 .
三、计算题
-
19. 解方程组20. 解不等式组: .21. 解不等式组:22. 解方程组:
四、综合题
-
23. 某商场在世博会上购置A,B两种玩具,其中B玩具的单价比A玩具的单价贵25元,且购置2个B玩具与1个A玩具共花费200元.(1)、求A,B玩具的单价;(2)、若该商场要求购置B玩具的数量是A玩具数量的2倍,且购置玩具的总额不高于20000元,则该商场最多可以购置多少个A玩具?24. 民生无小事,枝叶总关情,广东在“我为群众办实事”实践活动中推出“粤菜师傅”、“广东技工”、“南粤家政”三项培训工程,今年计划新增加培训共100万人次(1)、若“广东技工”今年计划新增加培训31万人次,“粤菜师傅”今年计划新增加培训人次是“南粤家政”的2倍,求“南粤家政”今年计划新增加的培训人次;(2)、“粤菜师傅”工程开展以来,已累计带动33.6万人次创业就业,据报道,经过“粤菜师傅”项目培训的人员工资稳定提升,已知李某去年的年工资收入为9.6万元,预计李某今年的年工资收入不低于12.48万元,则李某的年工资收入增长率至少要达到多少?25. 某校为了开展“阳光体育运动”,计划购买篮球、足球共60个,已知每个篮球的价格为70元,每个足球的价格为80元.(1)、若购买这两类球的总金额为4600元,求篮球、足球各买了多少个?(2)、若购买篮球的总金额不超过购买足球的总金额,求最多可购买多少个篮球?26. 平面直角坐标系 中,抛物线 过点 , , ,顶点 不在第一象限,线段 上有一点 ,设 的面积为 , 的面积为 , .(1)、用含 的式子表示 ;(2)、求点 的坐标;(3)、若直线 与抛物线 的另一个交点 的横坐标为 ,求 在 时的取值范围(用含 的式子表示).27. 已知关于 , 的方程组 与 的解相同.(1)、求 , 的值;(2)、若一个三角形的一条边的长为 ,另外两条边的长是关于 的方程 的解.试判断该三角形的形状,并说明理由.28. 有A,B两个发电厂,每焚烧一吨垃圾,A发电厂比B发电厂多发40度电,A焚烧20吨垃圾比B焚烧30吨垃圾少1800度电.(1)、求焚烧1吨垃圾,A和B各发电多少?(2)、A,B两个发电厂共焚烧90吨的垃圾,A焚烧的垃圾不多于B焚烧的垃圾两倍,求A厂和B厂总发电量最大为多少度?29. 端午节是我国入选世界非物质文化遗产的传统节日,端午节吃粽子是中华民族的传统习俗.市场上豆沙粽的进价比猪肉粽的进价每盒便宜10元,某商家用8000元购进的猪肉粽和用6000元购进的豆沙粽盒数相同.在销售中,该商家发现猪肉粽每盒售价50元时,每天可售出100盒;每盒售价提高1元时,每天少售出2盒.(1)、求猪肉粽和豆沙粽每盒的进价;(2)、设猪肉粽每盒售价x元 表示该商家每天销售猪肉粽的利润(单位:元),求y关于x的函数解析式并求最大利润.30. 某社区拟建 , 两类摊位以搞活“地摊经济”,每个 类摊位的占地面积比每个 类摊位的占地面积多2平方米,建 类摊位每平方米的费用为40元,建 类摊位每平方米的费用为30元,用60平方米建 类摊位的个数恰好是用同样面积建 类摊位个数的 .(1)、求每个 , 类摊位占地面积各为多少平方米?(2)、该社拟建 , 两类摊位共90个,且 类摊位的数量不少于 类摊位数量的3倍.求建造这90个摊位的最大费用.31. 某学校开展了社会实践活动,活动地点距离学校12km,甲、乙两同学骑自行车同时从学校出发,甲的速度是乙的1.2倍,结果甲比乙早到10min,求乙同学骑自行车的速度.32. 端午节前夕,某商铺用620元购进50个肉粽和30个蜜枣粽,肉粽的进货单价比蜜枣粽的进货单价多6元.(1)、肉粽和蜜枣粽的进货单价分别是多少元?(2)、由于粽子畅销,商铺决定再购进这两种粽子共300个,其中肉粽数量不多于蜜枣粽数量的2倍,且每种粽子的进货单价保持不变,若肉粽的销售单价为14元,蜜枣粽的销售单价为6元,试问第二批购进肉粽多少个时,全部售完后,第二批粽子获得利润最大?第二批粽子的最大利润是多少元?33. 探究:是否存在一个新矩形,使其周长和面积为原矩形的2倍、 倍、k倍.(1)、若该矩形为正方形,是否存在一个正方形,使其周长和面积都为边长为2的正方形的2倍?(填“存在”或“不存在”).(2)、继续探究,是否存在一个矩形,使其周长和面积都为长为3,宽为2的矩形的2倍?
同学们有以下思路:
①设新矩形长和宽为x、y , 则依题意 , ,
联立 得 ,再探究根的情况:
根据此方法,请你探究是否存在一个矩形,使其周长和面积都为原矩形的 倍;
②如图也可用反比例函数与一次函数证明 : , : ,那么,
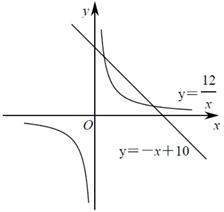
a . 是否存在一个新矩形为原矩形周长和面积的2倍?
b . 请探究是否有一新矩形周长和面积为原矩形的 ,若存在,用图像表达;
c . 请直接写出当结论成立时k的取值范围:.