2023-2024学年初中数学八年级上册 19.2 证明举例 同步分层训练培优卷(沪教版五四制)
试卷更新日期:2023-07-28 类型:同步测试
一、选择题
-
1. 甲、乙、丙3人从图书馆各借了一本书(如下表所示),他们相约在每个星期天相互交换读完的书,经过数次交换后,他们都读完了这3本书.已知甲读的第三本书是乙读的第二本书,则丙读的第二本书是( )
甲
乙
丙
书A
书B
书C
A、书A B、书B C、书C D、无法确定2. 用反证法求证:三角形中最多有一个钝角.下列假设正确的是( )A、假设三角形中至少有两个钝角 B、假设三角形中最多有两个钝角 C、假设三角形中最少有一个钝角 D、假设三角形中没有钝角3. 李明、王华、周亮和张红四名同学参加了“华罗庚杯”竞赛选拔赛,王华和张红两个同学的得分和等于周亮和李明的得分和;李明与王华的得分和大于周亮和张红的得分和,张红的得分超过周亮与王华的得分和,则这四位同学的得分由大到小的顺序是( )A、李明,张红,周亮,王华 B、李明,张红,王华,周亮 C、张红,李明,周亮,王华 D、张红,李明,王华,周亮4. 阅读下列材料,其中①~④步数学依据错误的是( )如图:已知直线 , a⊥b,求证: .
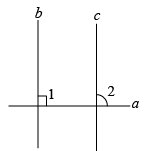
证明:∵(已知),
∴(①垂直的定义).
∵ (已知),
∴(②两直线平行,同位角相等),
∴(③同角的余角相等),
∴(④垂直的定义).
A、① B、② C、③ D、④5. 嘉淇在证明“平行于同一条直线的两条直线平行”时,给出了如下推理过程:已知:如图,b∥a,c∥a,求证:b∥c;
证明:作直线DF交直线a、b、c分
别于点D、E、F,
∵a∥b,∴∠1=∠4,又∵a∥c,
∴∠1=∠5,
∴b∥c.

小明为保证嘉淇的推理更严谨,想在方框中“∴∠1=∠5”和“∴b∥c”之间作补充,下列说法正确的是( )
A、嘉淇的推理严谨,不需要补充 B、应补充∠2=∠5 C、应补充∠3+∠5=180° D、应补充∠4=∠56. 桌子上有6只杯口朝上的茶杯,每次翻转其中的4只,经过 次翻转可使这6只杯子的杯口全部朝下,则 的最小值为( )A、 B、 C、 D、7. 若要运用反证法证明“若 , 则”,首先应该假设( )A、 B、 C、 D、8. 如图, , 为上一点, , 且平分 , 过点作于点 , 且 , 则下列结论:①;②;③平分;④平分 . 其中正确的是( )
 A、①② B、①②③ C、②③④ D、①②③④
A、①② B、①②③ C、②③④ D、①②③④二、填空题
-
9. 用反证法证明:在一个三角形中,如果两个角不相等,那么这两个角所对的边也不相等,证明时,可以先假设: .10. 反证法证明命题“同旁内角不互补的两条直线不平行”时,应先假设.11. 金乡县某中学七年级共有四个班,每班各选5名同学组成一个代表队,这四支代表队(分别用A,B,C,D表示)进行数学知识应用竞赛,前三名将参加金乡县数学知识竞赛,甲,乙,丙三位同学预测的结果分别为:甲:C得亚军;D得季军;乙:D得冠军;A得亚军;丙:C得冠军;B得亚军.已知每人的预测都是半句正确,半句错误,则冠,亚,季,殿军分别为 .12. “爆竹声中一岁除,春风送暖入屠苏.千门万户曈曈日,总把新桃换旧符.”春节将至,置办年货是中国寻常百姓家不可或缺的大事.小明随妈妈去置办年货,购买了灯笼、窗花、坚果,其中灯笼每只20元,窗花每张8元,坚果每包150元,若小明和妈妈一共用了428元(三种年货都有购买),则最多能买灯笼只.13. 为鼓励学生居家锻炼,李老师组织线上仰卧起坐接力活动.4人为一组,每人自主设定个人目标(单位:次),组内任意2人之间均需接力一场,且每场接力2人都达到个人目标即停止,记录每场接力成绩(2人所做仰卧起坐次数之和).小贾、小易、小冰、小丁为一组,他们六场接力成绩由小到大依次为86,92,94,98,100,106.若他们设定的个人目标分别记为a,b,c,d,其中 , 且 . 根据以上信息,得到三个结论:① , ;②六场接力成绩由小到大可以依次表示为: , , , , , ;③a,b,c,d的值分别为46,40,52,54.其中正确结论的序号是 .
三、解答题
-
14. 如图:EF∥AD ,∠1=∠2,∠BAC=70°,将求∠AGD的过程填写完整:
因为EF∥AD,所以∠2= ,
又因为∠1=∠2,所以∠1=∠3,
所以AB∥ ,
所以∠BAC+ =180°,
因为∠BAC=70°,所以∠AGD= .
 15. 请在下列括号内填上相应步骤或理由.
15. 请在下列括号内填上相应步骤或理由.已知:如图, , 垂足为A, .

试说明: .
解:因为(已知),
所以( ).
因为(已知),
所以 ▲ (等量代换).
所以( ).
所以( ).
因为(已知),
所以(垂直的定义).
所以( ).
所以(垂直的定义).
四、作图题
-
16. 数学课上,王老师布置如下任务:
如图,已知∠MAN<45°,点B是射线AM上的一个定点,在射线AN上求作点C,使∠ACB=2∠A.
下面是小路设计的尺规作图过程.
作法:①作线段AB的垂直平分线l,直线l交射线AN于点D;
②以点B为圆心,BD长为半径作弧,交射线AN于另一点C,则点C即为所求.

根据小路设计的尺规作图过程,
(1)、使用直尺和圆规,补全图形;(保留作图痕迹)(2)、完成下面的证明:证明:连接BD,BC,
∵直线l为线段AB的垂直平分线,
∴DA= ▲ , ( )(填推理的依据)
∴∠A=∠ABD,
∴∠BDC=∠A+∠ABD=2∠A.
∵BC=BD,
∴∠ACB=∠ ▲ , ( )(填推理的依据)
∴∠ACB=2∠A.
五、综合题
-
17.(1)、如图1,在△ABC中,D是AB上一点,E是AC上一点,BE、CD相交于点F , ∠A=62°,∠ACD=35°,∠ABE=20°.求:∠BFD的度数.对于上述问题,在以下解答过程的空白处填上适当的内容(理由或数学式).

解:∵∠BDC=∠A+∠ACD( ▲ ),
∴∠BDC=62°+35°=97°(等量代换).
∵∠BFD+∠BDC+∠ABE= ▲ ( ▲ ),
∴∠BFD=180°﹣∠BDC﹣∠ABE=180°﹣97°﹣20°=63°(等式的性质).
(2)、如图2,把一个长方形的纸ABCD沿对角线折叠(长方形对边平行且相等,四个角是直角),重合部分△FBD是个什么三角形?请证明你的结论.18. 设 , 是两个不相等的正整数,为质数,满足 , 且是整数.(1)、求证:;(2)、求的值;(3)、求 , 的值.
-