2023-2024学年初中数学八年级上册 19.1 命题与证明同步分层训练基础卷(沪教版五四制)

试卷更新日期：2023-07-28 类型：同步测试

进入出卷网下载

一、选择题

1. 下列命题属于假命题的是（）

A、三个角对应相等的两个三角形全等 B、三边对应相等的两个三角形全等 C、全等三角形的对应边相等 D、全等三角形的面积相等

查看试题解析
2. 下列语句是命题的是（）

A、作直线AB的垂线 B、在线段AB上取点C C、垂线段最短吗？ D、同旁内角互补

查看试题解析
3. 下列结论正确的是（）

A、有理数与数轴上的点一一对应 B、二次根式 $\sqrt{x^{2} + 1}$ 有意义条件是 $x > 0$ C、立方根等于它本身是 $\pm 1$ D、如果 $a^{3} = b^{3}$ ，那么 $a = b$

查看试题解析
4. 下列命题中是假命题的是（）.

A、同旁内角互补，两直线平行 B、直线 $\vec{a} ⊥ \vec{b}$ ，则a与b相交所成的角为直角 C、如果两个角互补，那么这两个角是一个锐角，一个钝角 D、若 $a ∥ b$ ， $a ⊥ c$ ，那么 $b ⊥ c$

查看试题解析
5. 对于命题“如果 $a^{2} > b^{2}$ ，那么 $a > b$ ”，下面四组关于a，b的值中，能说明这个命题是假命题的是（）

A、 $a = 3$ ， $b = - 2$ B、 $a = - 2$ ， $b = 3$ C、 $a = 3$ ， $b = 2$ D、 $a = - 3$ ， $b = 2$

查看试题解析
6. 如图， $∠ 1 = ∠ 2$ ， $A B ∥ C D$ ， $A B = A C = A E = C D$ ．有下列结论：
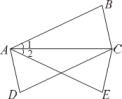
①把 $△ A B C$ 沿直线 $A C$ 翻折180°，可得到 $△ A E C$ ；
②把 $△ A D C$ 沿线段 $A C$ 的垂直平分线翻折180°，可得到 $△ A E C$ ；
③把 $△ A D C$ 沿射线DC方向平移与 $D C$ 相等的长度，可得到 $△ A B C$ ．
其中所有符合题意结论的序号是（）

A、①② B、①③ C、②③ D、①②③

查看试题解析
7. 有下列四个命题：①一次函数 $y = - 2 x + 4$ 的函数值随着x值的增大而增大；②等角的补角相等；③如果 $b ∥ a$ ， $c ∥ a$ ，那么 $b ∥ c$ ；④点 $M (- 2 ， 5)$ 关于x轴的对称点是N，则线段 $M N$ 的长是10，其中是真命题的有（）

A、4个 B、3个 C、2个 D、1个

查看试题解析
8. 下列语句中，是真命题的是（）

A、已知 $a^{2} = 4$ ，求a的值 B、面积相等的两个三角形全等 C、对顶角相等 D、若 $a > b$ ，则 $a^{2} > b^{2}$

查看试题解析

二、填空题

9. 将命题“线段垂直平分线上的点到线段两端的距离相等”改写成“如果……，那么……”的形式为．

查看试题解析
10. “若 $a b ＞ 0$ ，则 $a ＞ 0$ ， $b ＞ 0$ ”命题（选填“是”或“不是”）．

查看试题解析
11. 把命题“内错角相等”改成“如果……那么……”的形式．

查看试题解析
12. 能说明命题：“若两个角 $α$ ， $β$ 互补，则这两个角必为一个锐角一个钝角”是假命题的反例是.

查看试题解析
13. 在说明命题“若|a|＞3，则a＞3”是假命题的反例中，a的值可以是 .

查看试题解析

三、解答题

14. 以下是两位同学在复习不等式过程中的对话：
小明说：”不等式a> 2a永远都不会成立，因为如果在这个不等式两边同时除以a，就．会出现1>2这样的错误结论!”

小丽说：“如果a>b，c>d，那么一定会得出a-c>b-d．"

你认为小明的说法(填“正确”或“不正确”)；小丽的说法(填“正确”或“不正确”)，并选择其中一个人判断阐述你的理由(若认为正确，则进行证明；若认为不正确，则给出反例)．

查看试题解析

四、综合题

15. 求证：顶角是锐角的等腰三角形腰上的高与底边夹角等于其顶角的一半．

(1)、根据题意补全下图，并根据题设和结论，结合图形，用符号语言补充写出“已知”和“求证”．
已知：在锐角 $△ A B C$ 中， $A B = A C$ ， ▲ ；
求证： ▲ ．

(2)、证明：

查看试题解析
16. 如图，已知四个关系式：①AC＝DC；②BC＝EC；③∠DCA＝∠ECB：④AB＝DE．

(1)、从上面四个关系式中任取三个为条件，余下的一个为结论，组成一个命题．在组成的命题中真命题的个数是；

(2)、从（1）中选择一个真命题进行证明
已知：      ▲ ．
求证：      ▲ ．
证明：      ▲ ．

查看试题解析

2023-2024学年初中数学八年级上册 19.1 命题与证明 同步分层训练基础卷(沪教版五四制)

一、选择题

二、填空题

三、解答题

四、综合题

2023-2024学年初中数学八年级上册 19.1 命题与证明同步分层训练基础卷(沪教版五四制)