2023-2024学年初中数学八年级上册 18.4 函数的表示法 同步分层训练培优卷(沪教版五四制)
试卷更新日期:2023-07-28 类型:同步测试
一、选择题
-
1. 有一种手持烟花,点然后每隔 1.4 秒发射一发花弹。要求每一发花弹爆炸时的高度要超过 15 米,否则视为不合格,在一次测试实验中,该烟花发射出的第一发花弹的飞行高度(米)随飞行时间(秒)变化的规律如下表所示.下列这一变化过程中说法正确的是( )
 A、飞行时间 t每增加 0.5 秒,飞行高度 h 就增加 5.5 米 B、飞行时间 t 每增加 0.5 秒,飞行高度 h 就减少 5.5 米 C、估计飞行时间 t 为 5 秒时,飞行高度 h 为 11.8 米 D、只要飞行时间 t 超过 1.5 秒后该花弹爆炸,就视为合格2. 将二元一次方程 化成用x的代数式表示y的形式为( )A、 B、 C、 D、3. 一蓄水池中有水 ,打开排水阀门开始放水后水池的水量与放水时间有如下关系:
A、飞行时间 t每增加 0.5 秒,飞行高度 h 就增加 5.5 米 B、飞行时间 t 每增加 0.5 秒,飞行高度 h 就减少 5.5 米 C、估计飞行时间 t 为 5 秒时,飞行高度 h 为 11.8 米 D、只要飞行时间 t 超过 1.5 秒后该花弹爆炸,就视为合格2. 将二元一次方程 化成用x的代数式表示y的形式为( )A、 B、 C、 D、3. 一蓄水池中有水 ,打开排水阀门开始放水后水池的水量与放水时间有如下关系:
下列说法不正确的是( )
A、蓄水池每分钟放水 B、放水 分钟后,水池中水量为 C、蓄水池一共可以放水 分钟 D、放水 分钟后,水池中水量水量为4. 某地区用电量与应缴电费之间的关系如下表:则下列叙述错误的是( )用电量(千瓦•时)
1
2
3
4
…
应缴电费(元)
0.55
1.10
1.65
2.20
…
A、用电量每增加1千瓦•时,电费增加0.55元 B、若用电量为8千瓦•时,则应缴电费4.4元 C、若应缴电费为2.75元,则用电量为6千瓦•时 D、应缴电费随用电量的增加而增加5. 太原市第 37 中学校 A 同学在新冠疫情期间,妈妈每天为其测量体温,为了较直观地了 解这位同学这个月的日期和每天体温的变化趋势,可选择的比较好的方法是( )A、表格法 B、图象法 C、关系式法 D、以上三种方法均可6. 一列货运火车从某站出发,加速行驶一段时间后开始匀速行驶,过了一段时间,火车到达下一个车站停下,装完货后,火车又加速行驶,一段时间后再次开始匀速行驶,那么可以近似地刻画出火车在这段时间内的速度变化情况的是( )A、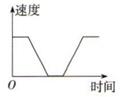 B、
B、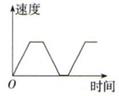 C、
C、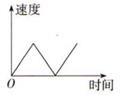 D、
D、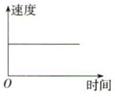 7. 如图,正方形和的周长之和为 , 设圆的半径为 , 正方形的边长为 , 阴影部分的面积为 . 当x在一定范围内变化时,y和S都随x的变化而变化,则y与x,S与x满足的函数关系分别是( )
7. 如图,正方形和的周长之和为 , 设圆的半径为 , 正方形的边长为 , 阴影部分的面积为 . 当x在一定范围内变化时,y和S都随x的变化而变化,则y与x,S与x满足的函数关系分别是( )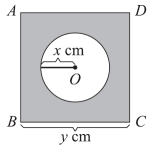 A、一次函数关系,一次函数关系 B、一次函数关系,二次函数关系 C、二次函数关系,二次函数关系 D、二次函数关系,一次函数关系8. 如果I表示汽车经撞击之后的损坏程度,经多次实验研究后知道,I与撞击时的速度v的平方之比是常数2,则I与v的函数关系为( )A、正比例函数关系 B、反比例函数关系 C、一次函数关系 D、二次函数关系
A、一次函数关系,一次函数关系 B、一次函数关系,二次函数关系 C、二次函数关系,二次函数关系 D、二次函数关系,一次函数关系8. 如果I表示汽车经撞击之后的损坏程度,经多次实验研究后知道,I与撞击时的速度v的平方之比是常数2,则I与v的函数关系为( )A、正比例函数关系 B、反比例函数关系 C、一次函数关系 D、二次函数关系二、填空题
-
9. 某地的温度T(℃)与海拔高度h(km)之间的关系如下所示:
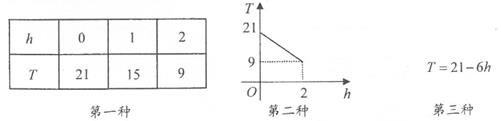
要算出海拔高度为6km时该地的温度,适宜用第种形式。
10. 长方形的周长为10cm , 其中一边为xcm(其中x>0),另一边为ycm , 则y关于x的函数表达式为 .11. 老师让同学们举一个y是x的函数的例子,同学们分别用表格、图象、函数关系式列举了如下4个x,y之间的关系:其中y一定是x的函数的是(填写所有正确的序号)
①
气温x
1
2
0
1
日期y
1
2
3
4
②
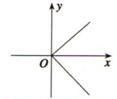
③y=kx+b(k,b为常数,k≠0)
④y=|x|
12. 点燃一根蜡烛后,蜡烛的高度h(厘米)与燃烧时间(分)之间的关系如表:则蜡烛的高度h(厘米)与燃烧时间(分)之间的关系式 ./分
0
2
4
6
8
10
h/厘米
30
29
28
27
26
25
三、解答题
-
13. 为了让学生养成热爱图书的习惯,某学校抽出一部分资金用于购买书籍.已知2020年该学校用于购买图书的费用为5000元,2022年用于购买图书的费用是7200元,求年买书资金的平均增长率.14. 在一次实验中,小明把一根弹簧的上端固定,在其下端悬挂物体,下表是测得的弹簧的长度y与所挂物体的质量x的几组对应值.
所挂物体
质量x/kg
0
1
2
3
4
5
弹簧长度
y/cm
18
20
22
24
26
28
①上述反映了哪两个变量之间的关系?哪个是自变量?哪个是因变量?②当所挂重物为3kg时,弹簧有多长?不挂重物呢?③若所挂重物为6kg时(在弹簧的允许范围内),你能说出此时弹簧的长度吗?
四、综合题
-
15. 拖拉机行驶过程中会对周围产生较大的噪声影响如图有一台拖拉机沿公路由点向点行驶,已知点为一所学校,且点与直线上两点 , 的距离分别为和 , 又 , 拖拉机周围以内为受噪声影响区域.
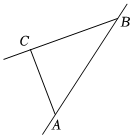 (1)、求度数;(2)、学校会受噪声影响吗?为什么?(3)、若拖拉机的行驶速度为每分钟米,拖拉机噪声影响该学校持续的时间有多少分钟?16. 据统计,某公交车每月的支出费用为3000元,每月利润(利润=票款收入-支出费用)(元)与每月的乘车人数(人)的变化关系如下表所示(公交车票价固定不变).
(1)、求度数;(2)、学校会受噪声影响吗?为什么?(3)、若拖拉机的行驶速度为每分钟米,拖拉机噪声影响该学校持续的时间有多少分钟?16. 据统计,某公交车每月的支出费用为3000元,每月利润(利润=票款收入-支出费用)(元)与每月的乘车人数(人)的变化关系如下表所示(公交车票价固定不变).每月乘车人数/人
600
900
1200
1500
1800
…
每月利润/元
-1800
-1200
-600
0
600
…
(1)、在这个变化过程中,自变量是 , 因变量是;(2)、观察表中数据可知,每月乘车人数达到人以上时,该公交车才不会亏损;(3)、由表中数据可推断出该公交车的票价为元;(4)、求每月乘车人数为5000人时的每月利润.