2023-2024学年初中数学八年级上册 17.4 一元二次方程的应用同步分层训练培优卷(沪教版五四制)

试卷更新日期：2023-07-28 类型：同步测试

进入出卷网下载

一、选择题

1. 某商场销售一种商品，原销售价为100元，为减少库存，经过两次降价，现销售价为81元，如果每次降价率都为x，则根据题意所列的方程正确的是（）.

A、 $81 (1 - x)^{2} = 100$ B、 $100 (1 - x)^{2} = 81$ C、 $100 (1 - 2 x) = 81$ D、 $100 （ 1 - x ） + 100 (1 - x)^{2} = 81$

查看试题解析
2. 2020年一2022年无锡居民人均可支配收入由5.76万元增长至6.58万元，设人均可支配收入的平均增长率为x，下列方程正确的是（）

A、 $5.76 (1 + x)^{2} = 6.58$ B、 $5.76 (1 + x^{2}) = 6.58$ C、 $5.76 (1 + 2 x) = 6.58$ D、 $5.76 x^{2} = 6.58$

查看试题解析
3. 某校“研学”活动小组在一次野外实践时，发现一种植物的 $1$ 个主干上长出 $x$ 个枝干，每个枝干上再长出 $x$ 个小分支 $.$ 若在一个主干上的主干，枝干和小分支的数量之和是 $57$ 个，则 $x$ 等于（）

A、 $5$ B、 $6$ C、 $7$ D、 $8$

查看试题解析
4. 某放射性元素经2天后，质量衰变为原来的 $\frac{1}{2}$ ．若设这种放射性元素质量的日平均减少率为 $x$ ，则可列出方程为（）

A、 $1 - 2 x = \frac{1}{2}$ B、 $2 (1 - x) = \frac{1}{2}$ C、 $(1 - x)^{2} = \frac{1}{2}$ D、 $\frac{1}{2} (1 - x)^{2} = 1$

查看试题解析
5. 为响应国家“双减政策”，某校2021年第三季度平均每周作业时长为600分钟，经过2021年第四季度和2022年第一季度两次整改后，平均每周作业时长为350分钟．设每季度平均每周作业时长的下降率为a，则可列方程为（）

A、 $600 (1 - a) = 350$ B、 $350 (1 + a) = 600$ C、 $600 {(1 - a)}^{2} = 350$ D、 $350 {(1 + a)}^{2} = 600$

查看试题解析
6. 某商品一月份售价100元，二月份涨价 $x %$ ，三月份再次涨价 $0.5 x %$ 后售价132元，下列所列方程正确的是（　　）

A、 $100 (1 + x %) (1 + 0.5 x %) = 132$ B、 $100 (1 + x %) \cdot 0.5 x % = 132$ C、 $100 (1 + x % + 0.5 x %) = 132$ D、 $100 (1 + x %) + 100 (1 + 0.5 x %) = 132$

查看试题解析
7. 如图，《九章算术》中的“折竹抵地”问题：今有竹高一丈，末折抵地，去高六尺，折高者几何？意思是：一根竹子，原高一丈（一丈＝十尺），一阵风将竹子折断，竹梢恰好抵地，抵地处离竹子底部6尺远，求折断处离地面的高度．设竹子折断处离地面x尺，根据题意，可列方程为（　　）

A、 $x^{2} + 6^{2} = 1 0^{2}$ B、 $（ 10 - x)^{2} + 6^{2} = x^{2}$ C、 $x^{2} + (10 - x)^{2} = 6^{2}$ D、 $x^{2} + 6^{2} = (10 - x)^{2}$

查看试题解析
8. 已知 $a$ ， $b$ ， $c$ 是1，3，4中的任意一个数（ $a$ ， $b$ ， $c$ 互不相等），当方程 $a x^{2} - b x + c = 0$ 的解均为整数时，以1，3和此方程的所有解为边长能构成的多边形一定是（）

A、轴对称图形 B、中心对称图形 C、轴对称图形或中心对称图形 D、非轴对称图形或中心对称图形

查看试题解析

二、填空题

9. 《九章算术》中提出了如下问题：今有户不知高、广，竿不知长短，横之不出四尺，从之不出二尺，邪之适出，问户高、广、邪各几何？这段话的意思是：今有门不知其高宽：有竿，不知其长短，横放，竿比门宽长出4尺：竖放，竿比门高长出2尺：斜放，竿与门对角线恰好相等．问门高、宽和对角线的长各是多少？则该问题中的门高是尺．

查看试题解析
10. 某学校生物兴趣小组在该校空地上围了一块面积为200m²的矩形试验田，用来种植蔬菜．如图，试验田一面靠墙，墙长35m，另外三面用49m长的篱围成，其中一边开有一扇1m宽的门（不包括篱笆）．设试验田垂直于墙的一边AB的长为xm，则所列方程为__ ．

查看试题解析
11. 在学校劳动实践基地里有一块长20米、宽10米的长方形菜地，为了管理方便，准备沿平行于两边的方向纵、横开辟三条等宽的小道（如图中阴影部分所示），剩下部分种植蔬菜，已知种植蔬菜的面积为171平方米，则小道的宽为米．

查看试题解析
12. 某校截止到 $2022$ 年底，校园绿化面积为 $1000$ 平方米．为美化环境，该校计划 $2024$ 年底绿化面积达到 $1440$ 平方米．利用方程想想，设这两年绿化面积的年平均增长率为 $x$ ，则依题意列方程为．

查看试题解析
13. 有一个正方形的花园，如果它的边长增加 $2 m$ ，那么花园面积将增加 $16 m^{2}$ ，则原花园的面积为．

查看试题解析

三、解答题

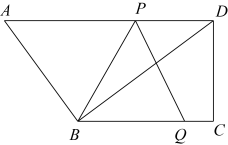
14. 如图，在直角梯形 $A B C D$ 中， $A D ∥ B C$ ， $∠ C = 90 °$ ， $B C = 16$ ， $D C = 12$ ， $A D = 21$ ．动点 $P$ 从点 $D$ 出发，沿射线 $D A$ 的方向以每秒2个单位的速度运动，动点 $Q$ 从点 $C$ 出发，沿射线 $C B$ 的方向以每秒1个单位的速度向点 $B$ 运动，点 $P$ ， $Q$ 分别从点 $D$ ， $C$ 同时出发，当点 $P$ 运动到点 $A$ 时，点 $Q$ 随之停止运动．设运动的时间为 $t$ （秒），当 $t$ 为何值时，以 $B$ ， $P$ ， $Q$ 三点为顶点的三角形是等腰三角形？

查看试题解析

15. 嘉海学校八年级开展社会实践活动，下表是“遇数临风”小组的记录表，请根据相关信息解决表中的两个问题．

嘉海学校社会实践记录表
团队名称	遇数临风	活动时间	$2023.4.26$
班级人员	$802$ 王嘉、马俊、张宁	地点	城南蔬菜超市
实践内容	调查青菜行情，帮超市解决销售问题的同时为顾客谋实惠．
调研信息	青菜的进价为2元/千克．
	青菜售价为 $2.5$ 元/千克时，每天可销售 $125$ 千克．
	每千克每涨价 $0.1$ 元，每天少销售5千克．
解决问题	问题1	某天超市正好销售 $105$ 千克的青菜，则获利多少元？
	问题2 若超市想一天销售青菜获利 $100$ 元，则青菜的售价为多少元/千克？

查看试题解析

四、综合题

16. 如图，在 $△$ ABC中，∠B＝90°，AB=6cm，AC=10cm，点P从点A开始沿AB向点B以1cm/s的速度移动，点Q从B点开始沿BC向点C以2cm/s的速度移动，P、Q两点同时出发，当一个点到达终点时另一个点也随之停止运动，运动时间为t．

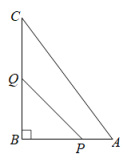(1)、几秒后四边形APQC的面积是19平方厘米；

(2)、若用S表示四边形APQC的面积，经过多长时间S取得最小值，并求出S的最小值．

查看试题解析
17. 阅读下列材料，并完成相应的任务．
古希腊的几何学家海伦在他的著作《度量论》一书中给出了利用三角形三边之长求面积的公式﹣﹣﹣﹣海伦公式S＝ $\sqrt{p (p - a) (p - b) (p - c)}$ （其中a ， b ， c是三角形的三边长， $p = \frac{a + b + c}{2}$ ，S为三角形的面积），并给出了证明

例如：在△ABC中，a＝3，b＝4，c＝5，那么它的面积可以这样计算：

∵a＝3，b＝4，c＝5

∴ $p = \frac{a + b + c}{2}$ ＝6

∴S＝ $\sqrt{p (p - a) (p - b) (p - c)}$ ＝ $\sqrt{6 \times 3 \times 2 \times 1}$ ＝6

事实上，对于已知三角形的三边长求三角形面积的问题，还可用我国南宋时期数学家秦九韶提出的秦九韶公式等方法解决．

根据上述材料，解答下列问题：

如图，在△ABC中，BC＝7，AC＝8，AB＝9

(1)、用海伦公式求△ABC的面积；

(2)、如图，AD、BE为△ABC的两条角平分线，它们的交点为I ，求△ABI的面积．

查看试题解析

2023-2024学年初中数学八年级上册 17.4 一元二次方程的应用 同步分层训练培优卷(沪教版五四制)

一、选择题

二、填空题

三、解答题

四、综合题

2023-2024学年初中数学八年级上册 17.4 一元二次方程的应用同步分层训练培优卷(沪教版五四制)