2023-2024学年初中数学八年级上册 17.3 一元二次方程根的判别式 同步分层训练培优卷(沪教版五四制)
试卷更新日期:2023-07-28 类型:同步测试
一、选择题
-
1. 若一元二次方程有解,则m的取值范围是( )A、 B、 C、且 D、且2. 关于x的一元二次方程的根的情况是( )A、有两个不相等的实数根 B、有两个相等的实数根 C、只有一个实数根 D、没有实数根3. 若一元二次方程有实数解,则m的取值范围是( )A、 B、 C、且 D、且4. 一元二次方程根的情况为( )A、有两个不相等的实数根 B、有两个相等的实数根 C、没有实数根 D、不能判定5. 关于x的一元二次方程根的情况,下列说法中正确的是( )A、有两个不相等的实数根 B、有两个相等的实数根 C、没有实数根 D、无法确定6. 对于一元二次方程 , 下列说法:
①若 , 则;
②若方程有两个不相等的实根,则方程必有两个不相等的实根;
③若c是方程的一个根,则一定有成立;
④若是一元二次方程的根,则其中正确的( )
A、只有①②④ B、只有①②③ C、①②③④ D、只有①②7. 对于一元二次方程 下列说法:①当 时,则方程 一定有一根为 ;②若 则方程 一定有两个不相等的实数根;③若c是方程 的一个根,则一定有 ;④若 ,则方程 有两个不相等的实数根.其中正确的是( )A、①② B、①③ C、①②④ D、②③④8. 已知关于x的一元二次方程 与 ,下列判断错误的是( )A、若方程 有两个实数根,则方程 也有两个实数根; B、如果m是方程 的一个根,那么 是 的一个根; C、如果方程 与 有一个根相等,那么这个根是1; D、如果方程 与 有一个根相等,那么这个根是1或-1.二、填空题
-
9. 已知关于x的一元二次方程(a-3)x2-8x+9=0.(1)、若方程的一个根为x=-1,则a的值为 ;(2)、若方程有实数根,则满足条件的正整数a的值为 .10. 若一元二次方程满足且有两个相等实数根,则a与c的关系是 .11. 对于代数式( , a,b,c为常数)①若 , 则有两个相等的实数根;②存在三个实数 , 使得;③若与方程的解相同,则 , 以上说法正确的是 .12. 如图是一块矩形菜地ABCD,AB=a(m),AD=b(m),面积为.现将边AB增加1m.
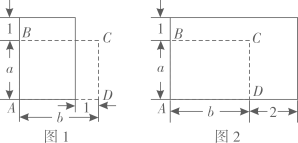 (1)、如图1,若a=5,边AD减少1m,得到的矩形面积不变,则b的值是.(2)、如图2,若边AD增加2m,有且只有一个a的值,使得到的矩形面积为 , 则s的值是.13. 若关于x的一元二次方程 各项系数满足 ,则此方程的根的情况:①必有两个不相等的实数根;②当 时,有两个相等的实数根;③当a , c同号时,方程有两个正的实数根;④当a , b同号时,方程有两个异号实数根.其中结论正确的个数是个.14. 已知实数
(1)、如图1,若a=5,边AD减少1m,得到的矩形面积不变,则b的值是.(2)、如图2,若边AD增加2m,有且只有一个a的值,使得到的矩形面积为 , 则s的值是.13. 若关于x的一元二次方程 各项系数满足 ,则此方程的根的情况:①必有两个不相等的实数根;②当 时,有两个相等的实数根;③当a , c同号时,方程有两个正的实数根;④当a , b同号时,方程有两个异号实数根.其中结论正确的个数是个.14. 已知实数 满足
满足 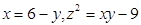 ,则 的值是.
,则 的值是. 三、计算题
-
15. 设一元二次方程 . 在下面的四组条件中选择其中一组的值,使这个方程有两个不相等的实数根,并解这个方程.
①;②;③;④ .
四、解答题
-
16. 已知矩形ABCD两邻边AB、BC的长是关于x的方程的两个实数根.当m为何值时,矩形ABCD的两邻边AB、BC的长相等.17. 已知关于x的方程有两个实数根 , , 求的取值范围.
五、综合题
-
18. 已知抛物线的顶点在轴上.(1)、求的值;(2)、求的值.19. 定义:若两个一元二次方程有且只有一个相同的实数根,我们就称这两个方程为“同伴方程”.例如x2=4和(x-2)(x+3)=0有且只有一个相同的实数根x=2,所以这两个方程为“同伴方程”.(1)、根据所学定义,下列方程属于“同伴方程”的有:(只填写序号即可)
① ②x2+4x+4=0 ③
(2)、关于x的一元二次方程x2-2x=0与x2+x+m-1=0为“同伴方程”,求m的值;(3)、若关于x的一元二次方程ax2+bx+c=0(a≠0)同时满足a-b+c=0和9a+3b+c=0,且与(x-n)(x+3)=0互为“同伴方程”,求n的值.
-