2023-2024学年初中数学七年级上册 10.2 分式的基本性质同步分层训练培优卷(沪教版五四制)

试卷更新日期：2023-07-28 类型：同步测试

进入出卷网下载

一、选择题

1. 在分式 $\frac{a + b}{a b}$ 中，把 $a 、 b$ 的值分别变为原来的2倍，则分式的值（）

A、不变 B、变为原来的2倍 C、变为原来的 $\frac{1}{2}$ D、变为原来的4倍

查看试题解析
2. 若把分式 $\frac{2 x}{y}$ 中x和y的值都扩大3倍，则分式的值（）

A、不变 B、扩大为原来的3倍 C、缩小为原来的 $\frac{1}{3}$ D、扩大为原来的9倍

查看试题解析
3. 把分式 $\frac{3 m n}{m + n}$ 中的 $m$ 、 $n$ 都扩大到原来的8倍，那么此分式的值（）

A、是原来的8倍 B、是原来的4倍 C、是原来的 $\frac{1}{8}$ D、不变

查看试题解析
4. 如果把分式 $\frac{x y}{3 x - y}$ 中的x，y都扩大3倍，那么分式的值（）

A、缩小3倍 B、不变 C、扩大3倍 D、扩大9倍

查看试题解析
5. 代数式 $(\frac{a^{2}}{a - 2} - a) \div \frac{1}{a - 2}$ 化简结果正确的是（）

A、 $2 a$ B、 $- 2 a$ C、 $2 a^{2} - 2 a$ D、 $2 a^{2} + 2 a$

查看试题解析
6. 若 $\frac{1}{2 y^{2} + 3 y + 7}$ 的值为 $\frac{1}{8}$ ,则 $\frac{1}{4 y^{2} + 6 y - 9}$ 的值是（）

A、 $- \frac{1}{2}$ B、 $- \frac{1}{17}$ C、 $- \frac{1}{7}$ D、 $\frac{1}{7}$

查看试题解析
7. 已知 $\frac{1}{a} - \frac{1}{b} = 4$ ，则 $\frac{a - 2 a b - b}{2 a - 2 b + 7 a b}$ 的值等于

A、6 B、 $- 6$ C、 $\frac{2}{15}$ D、 $- \frac{2}{7}$

查看试题解析
8. 将甲、乙、丙三个正分数化为最简分数后，其分子分别为6、15、10，其分母的最小公倍数为360．判断甲、乙、丙三数的大小关系为何？（）

A、乙＞甲＞丙 B、乙＞丙＞甲 C、甲＞乙＞丙 D、甲＞丙＞乙

查看试题解析

二、填空题

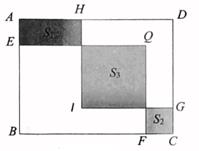
9. 不改变分式的值，将分式 $\frac{1 - \frac{1}{3} a}{1 - a}$ 的分子与分母的最高次项的系数化为正整数所得结果为．

查看试题解析
10. $\frac{1}{3 y^{2}}$ ， $\frac{4}{x y}$ 和 $\frac{5}{2 x^{2} y}$ 的最简公分母是.

查看试题解析
11. $\frac{2}{3 x^{2} (x - y)} ， \frac{2}{3 x - 3 y} ， \frac{1}{2 x y}$ 的最简公分母是 .

查看试题解析
12. 如图，在长方形ABCD中，AB=10，BC=13．E，F，G，H分别是线段AB，BC，CD，AD上的定点．现分别以BE，BF为边作长方形BEQF，以DG为边作正方形DGIH．若长方形BEQF与正方形DGIH的重合部分恰好是一个正方形，且BE=DG，Q，I均在长方形ABCD内部．记图中的阴影部分面积分别为S₁ ， S₂ ， S₃ ．若 $\frac{S_{2}}{S_{1}} = \frac{3}{7}$ ，则S₃= ．

查看试题解析
13. 阅读下面的材料，并解答问题：
分式 $\frac{2 x + 8}{x + 2}$ （ $x \geq 0$ ）的最大值是多少？

解： $\frac{2 x + 8}{x + 2} = \frac{2 x + 4 + 4}{x + 2} = \frac{2 (x + 2)}{x + 2} + \frac{4}{x + 2} = 2 + \frac{4}{x + 2}$ ，

因为x≥0，所以x+2的最小值是2，所以 $\frac{1}{x + 2}$ 的最大值是 $\frac{1}{2}$ ，所以 $2 + \frac{4}{x + 2}$ 的最大值是4，即 $\frac{2 x + 8}{x + 2}$ （x≥0）的最大值是4．

根据上述方法，试求分式 $\frac{2 x^{2} + 5}{x^{2} + 1}$ 的最大值是.

查看试题解析

三、解答题

14. 阅读下面材料，并解答问题.
将分式 $\frac{x^{4} + x^{2} - 3}{x^{2} - 1}$ 拆分成一个整式与一个分式（分子为整数）的和的形式.

解：由分母为x²﹣1，可设x⁴+x²﹣3＝（x²﹣1）（x²+a）+b.

则x⁴+x²﹣3＝（x²﹣1）（x²+a）+b＝x⁴﹣x²+ax²﹣a+b＝x⁴+（a﹣1）x²﹣a+b

∴ ${\begin{cases} a - 1 = 1 \\ - a + b = - 3 \end{cases}$ ，∴ ${\begin{cases} a = 2 \\ b = - 1 \end{cases}$

∴ $\frac{x^{4} + x^{2} - 3}{x^{2} - 1}$ ＝ $\frac{(x^{2} - 1) (x^{2} + 2) - 1}{x^{2} - 1}$ ＝ $\frac{(x^{2} - 1) (x^{2} + 2)}{x^{2} - 1}$ ﹣ $\frac{1}{x^{2} - 1}$ ＝（x²+2）﹣ $\frac{1}{x^{2} - 1}$

这样，分式 $\frac{x^{4} + x^{2} - 3}{x^{2} - 1}$ 被拆分成了一个整式x²+2与一个分式﹣ $\frac{1}{x^{2} - 1}$ 的和.

根据上述作法，将分式 $\frac{x^{4} + 6 x^{2} - 8}{x^{2} - 1}$ 拆分成一个整式与一个分式（分子为整数）的和的形式.

查看试题解析
15. 不改变分式的值，把下列分式的分子、分母中各项的系数化为整数．
（1） $\frac{\frac{1}{5} x - \frac{1}{10} y}{\frac{1}{3} x + \frac{1}{9} y}$ （2） $\frac{\frac{1}{2} x + \frac{1}{4} y}{\frac{1}{2} x - \frac{1}{3} y}$ ．

查看试题解析

四、综合题

16. 阅读：在分式中，当分子的次数大于或等于分母的次数时，我们称之为“假分式”，例如： $\frac{x - 1}{x + 1} ， \frac{x^{2}}{x + 2}$ 这样的分式就是假分式；当分子的次数小于分母的次数时，我们称之为“真分式”，例如： $\frac{1}{x + 1}$ ， $- \frac{2 x}{x^{2} - 1}$ 这样的分式就是真分式，我们知道，假分数可以化为带分数，例如： $\frac{8}{3} = \frac{3 \times 2 + 2}{3} = 3 \frac{2}{3}$ ，类似地，假分式也可以化为“带分式”，即整式与真分式的和的形式，
例如： $\frac{x^{2} + 2 x - 1}{x + 2} = \frac{x (x + 2) - 1}{x + 2} = x - \frac{1}{x + 2} ； \frac{x^{2}}{x + 2} = \frac{(x^{2} + 2 x) - 2 x}{x + 2} = \frac{x (x + 2) - 2 x - 4}{x + 2} = \frac{x (x + 2)}{x + 2} \frac{- 2 (x + 2) + 4}{x + 2} = x - 2 + \frac{4}{x + 2}$ ．

请根据上述材料，解答下列问题：

(1)、填空： $①$ 分式 $\frac{2}{x + 2}$ 是分式 $($ 填“真”或“假” $)$ ；
$②$ 把下列假分式化成一个整式与一个真分式的和 $($ 差 $)$ 的形式：
$\frac{x^{2} + 2 x - 13}{x - 3} =$ $+$ ．

(2)、把分式 $\frac{x^{2} + 2 x - 13}{x - 3}$ 化成一个整式与一个真分式的和 $($ 差 $)$ 的形式，并求 $x$ 取何整数时，这个分式的值为整数．

(3)、一个三位数 $m$ ，个位数字是百位数字的两倍，另一个两位数 $n$ ，十位数字与 $m$ 的百位数字相同，个位数字与 $m$ 的十位数字相同 $.$ 若这个三位数的平方能被这个两位数整除，求满足条件的两位数 $n$ ．

查看试题解析
17. 我们知道，假分数可以化为整数与真分数的和的形式，例如： $\frac{3}{2} = 1 + \frac{1}{2}$ ，在分式中，对于只含有一个字母的分式，当分子的次数大于或等于分母的次数时，我们称之为“假分式”；当分子的次数小于分母的次数时，我们称之为“真分式”．
例如： $\frac{x + 1}{x - 2}$ ， $\frac{x^{2}}{x + 2} \cdot \cdot \cdot \cdot \cdot$ 像这样的分式是假分式；像 $\frac{1}{x - 2}$ ， $\frac{x}{x^{2} - 1} \cdot \cdot \cdot \cdot \cdot$ 这样的分式是真分式，类似的，假分式也可以化为整式与真分式的和的形式．例如： $\frac{x + 1}{x - 2} = \frac{(x - 2) + 3}{x - 2} = 1 + \frac{3}{x - 2}$ ； $\frac{x^{2}}{x + 2} = \frac{(x + 2) (x - 2) + 4}{x + 2} = x - 2 + \frac{4}{x + 2}$ ，解决下列问题：

(1)、将分式 $\frac{x - 2}{x + 3}$ 化为整式与真分式的和的形式为：（直接写出结果即可）

(2)、如果分式 $\frac{x^{2} + 2 x}{x + 3}$ 的值为整数，求 $x$ 的整数值

查看试题解析

2023-2024学年初中数学七年级上册 10.2 分式的基本性质 同步分层训练培优卷(沪教版五四制)

一、选择题

二、填空题

三、解答题

四、综合题

2023-2024学年初中数学七年级上册 10.2 分式的基本性质同步分层训练培优卷(沪教版五四制)