2023-2024学年初中数学七年级上册9.10 整式的乘法 同步分层训练培优卷(沪教版五四制)
试卷更新日期:2023-07-28 类型:同步测试
一、选择题
-
1. 计算:的结果是( )A、 B、 C、 D、2. 若多项式可分解为 , 则的值为( )A、-11 B、11 C、-3 D、33. 如图,四位同学给出了四种表示该长方形面积的多项式,

①
②
③
④
你认为其中正确的有( )
A、①② B、③④ C、①②③ D、①②③④4. 计算:( )A、 B、 C、 D、5. 把多项式x2+ax+b分解因式,得(x+1)(x-3),则a、b的值分别是( )A、a=2,b=3 B、a=-2,b=-3 C、a=-2,b=3 D、a=2,b=-36. 设有边长分别为a和b()的A类和B类正方形纸片、长为a宽为b的C类矩形纸片若干张.如图所示要拼一个边长为的正方形,需要1张A类纸片、1张B类纸片和2张C类纸片.若要拼一个长为、宽为的矩形,则需要C类纸片的张数为( ) A、6 B、7 C、8 D、97. 若 , 则 , 的值分别是( )A、 , B、 , C、 , D、 ,8. 如图1的8张宽为a,长为 的小长方形纸片,按如图2的方式不重叠地放在长方形ABCD内,未被覆盖的部分(两个长方形)用阴影表示.设左上角与右下角的阴影部分的面积的差为S,当BC的长度变化时,按照同样的放置方式,S始终保持不变,则a,b满足( )
A、6 B、7 C、8 D、97. 若 , 则 , 的值分别是( )A、 , B、 , C、 , D、 ,8. 如图1的8张宽为a,长为 的小长方形纸片,按如图2的方式不重叠地放在长方形ABCD内,未被覆盖的部分(两个长方形)用阴影表示.设左上角与右下角的阴影部分的面积的差为S,当BC的长度变化时,按照同样的放置方式,S始终保持不变,则a,b满足( )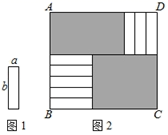 A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
9. 若 , 则.10. 一个多项式与的积为 , 则.11. 用纸片拼图时,我们发现利用图1中的三种纸片(边长分别为 , 的正方形和长为 宽为 的长方形)各若干,可以拼出一些长方形来解释某些等式,比如图2可以解释为: .
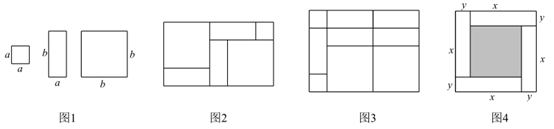 (1)、图3可以解释为等式:;(2)、要拼出一个两边长为 , 的长方形,先回答需要以下三种纸片各多少块,再用画图或整式乘法验证你的结论;
(1)、图3可以解释为等式:;(2)、要拼出一个两边长为 , 的长方形,先回答需要以下三种纸片各多少块,再用画图或整式乘法验证你的结论; 块,
块,  块,
块,  块(3)、如图4,大正方形的边长为 ,小正方形的边长为 ,若用 , ( )表示四个相同小长方形的两边长,以下关系式正确的是 (填序号).① ;② ;③ ;④ .12. 现有A、B、C三种型号的地板砖,其规格如图所示,若用这三种地板砖铺设一个长为 ,宽为 的长方形地面,则需要B种地砖块.
块(3)、如图4,大正方形的边长为 ,小正方形的边长为 ,若用 , ( )表示四个相同小长方形的两边长,以下关系式正确的是 (填序号).① ;② ;③ ;④ .12. 现有A、B、C三种型号的地板砖,其规格如图所示,若用这三种地板砖铺设一个长为 ,宽为 的长方形地面,则需要B种地砖块.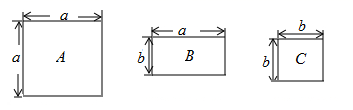 13. 如图,现有A,C两类正方形卡片和B类长方形卡片各若干张,用它们可以拼成一些新的长方形.如果要拼成一个长为(3a+b),宽为(a+2b)的长方形,那么需要B类长方形卡片张.
13. 如图,现有A,C两类正方形卡片和B类长方形卡片各若干张,用它们可以拼成一些新的长方形.如果要拼成一个长为(3a+b),宽为(a+2b)的长方形,那么需要B类长方形卡片张.
三、计算题
-
14. 计算:
四、解答题
-
15. 若的积中不含项与项,求、的值;16. 小马虎同学在进行两个多项式的乘法时,不小心把乘以 , 错抄成除以 , 结果得 , 则第一个多项式是多少?
五、综合题
-
17. 我们知道,根据几何图形的面积关系可以说明一些等式的成立.
例如:可以用图1的面积关系来说明.
 (1)、根据图2写出一个等式;(2)、请你再举一个例子,写出等式并在图3空白处画出一个相应的几何图形加以说明 (注:不必证明,用代数式标出各部分面积即可).18.(1)、通过计算几何图形的面积可以表示一些代数恒等式,甲图是边长为的正方形,
(1)、根据图2写出一个等式;(2)、请你再举一个例子,写出等式并在图3空白处画出一个相应的几何图形加以说明 (注:不必证明,用代数式标出各部分面积即可).18.(1)、通过计算几何图形的面积可以表示一些代数恒等式,甲图是边长为的正方形,
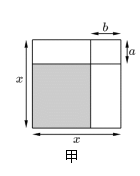
请用两种不同的方法表示甲图中阴影部分的面积( , 为常数)
①因式的积的形式:;
②关于的二次多项式的形式:;由①与②,可以得到一个等式:.
(2)、由(1)的结果进行应用:若对的任何值都成立,求 , 的值(3)、事实上,通过计算几何图形的体积也可以表示一些代数恒等式,乙图表示的是一个边长为的正方体挖去一个小长方体后重新拼成一个新长方体,请你根据乙图中图形的变化关系,利用整式乘法写出一个代数恒等式.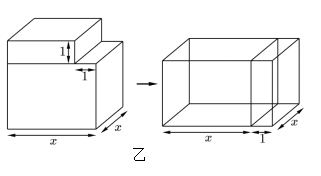
-