2023-2024学年初中数学七年级上册 11.6 轴对称同步分层训练培优卷(沪教版五四制)

试卷更新日期：2023-07-28 类型：同步测试

进入出卷网下载

一、选择题

1. 如图是嘉嘉把纸折叠后剪出的图案，将剪纸展开后得到的图案是（　　）

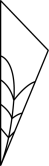A、 B、 C、 D、

查看试题解析
2. 已知点 $Р (2 ， a)$ 与 $Q (2 ， b)$ 关于x轴对称，则 $a + b =$ （）

A、1 B、0 C、4 D、2

查看试题解析
3. 如图，在△ABC中，已知AB＝8，点D、E分别在边AC、AB上，现将△ADE沿直线DE折叠，使点A恰好落在点F处，若将线段BC向左平移刚好可以与线段EF重合，连结CF.若2BC+CF＝15，则BC-2CF的值为（）

A、4 B、5 C、6 D、7

查看试题解析
4. 如图，已知 $∠ B A C = 32 °$ ，点 $D$ 、 $E$ 分别在 $A B$ 、 $A C$ 边上，将 $△ A D E$ 沿 $D E$ 折叠，点 $A$ 落在 $∠ B A C$ 外部的点 $A$ 处，此时测得 $∠ 1 = 106 °$ ，则 $∠ 2$ 的度数为（）

A、 $34 °$ B、 $37 °$ C、 $40 °$ D、 $42 °$

查看试题解析
5. 如图，把一张长方形的纸按图那样折叠后，B，D两点落在 $B^{'}$ ， $D^{'}$ 点处，若得 $∠ A O B^{'} = 70 °$ ，则 $∠ O G C$ 的度数为（）．

A、55° B、35° C、70° D、60°

查看试题解析
6. 若坐标平面上点P(a，1)与点Q(-4，b)关于x轴对称，则（）

A、a=4，b=-1 B、a=-4，b=1 C、a=-4，b=-1 D、a=4，b=1

查看试题解析
7. 如图，长方形 $A B C D$ 中，点 $E$ 为 $A D$ 上一点，连接 $C E$ ，将长方形 $A B C D$ 沿着直线 $C E$ 折叠，点 $D$ 恰好落在 $A B$ 的中点 $F$ 上，点 $G$ 为 $C F$ 的中点，点 $P$ 为线段 $C E$ 上的动点，连接 $P F$ 、 $P G$ ，若 $A E = a$ 、 $E D = b$ 、 $A F = c$ ，则 $P F + P G$ 的最小值是（）

A、 $a + c - b$ B、 $b + 2 c$ C、 $a + b + 2 c$ D、 $a + b$

查看试题解析
8. 如图，在△ABC中，AB＝AC．在AB、AC上分别截取AP、AQ，使AP＝AQ．再分别以点P，Q为圆心，以大于 $\frac{1}{2}$ PQ的长为半径作弧，两弧在∠BAC内交于点R，作射线AR，交BC于点D．已知BC＝5，AD=6．若点M、N分别是线段AD和线段AC上的动点，则CM+MN的最小值为（）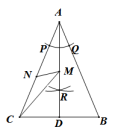

A、4 B、5 C、 $\frac{60}{13}$ D、2 $\sqrt{6}$

查看试题解析

二、填空题

9. 一张长方形纸片沿直线 $A B$ 折成如图所示图案，已知 $∠ 1 = 50 °$ ，则 $∠ O B A =$ __．

查看试题解析
10. 平面直角坐标系中，点 $P (3 ， - 2)$ 关于点 $Q (1 ， 0)$ 成中心对称的点的坐标是．

查看试题解析
11. 如图，在三角形纸片 $A B C$ 中， $A B = A C ， ∠ B = 20 °$ ，点 $D$ 是边 $B C$ 上的动点，将三角形纸片沿 $A D$ 对折，使点 $B$ 落在点 $B^{'}$ 处，当 $B^{'} D ⊥ B C$ 时， $∠ B A D$ 的度数为．

查看试题解析
12. 如图，长方形 $A B C D$ 中，点 $E$ 、 $F$ 分别在边 $A B$ 、 $C D$ 上，连接 $E F$ ，将 $∠ B E F$ 对折，点 $B$ 落在直线 $E F$ 上的点 $B^{'}$ 处，得折痕 $E M$ ，将 $∠ A E F$ 对折，点 $A$ 落在直线 $E F$ 上的点 $A^{'}$ 处，得折痕 $E N$ ，点 $G$ 在 $C D$ 上， $∠ N E G = 2 ∠ M E G$ ， $2 ∠ F E G = 3 ∠ A E N$ ，则 $∠ B E M$ 为度.

查看试题解析

三、解答题

13. 三角形ABC为等腰直角三角形，其中∠A=90°，BC长为6.
　　( 1 )建立适当的直角坐标系，并写出各个顶点的坐标；
　　( 2 )将(1)中各顶点的横坐标都加2，纵坐标保持不变，与原图案相比，所得的图案有什么变化？
　　( 3 )将(1)中各顶点的横坐标不变，将纵坐标都乘-1，与原图案相比，所得的图案有什么变化？
　　( 4 )将(1)中各顶点的横坐标都乘-2，纵坐标保持不变，与原图案相比，所得的图案有什么变化？

查看试题解析
14. 在 $6 \times 6$ 的网格中已经涂黑了三个小正方形，请在图中涂黑一块（或两块）小正方形，使涂黑的四个（或五个）小正方形组成一个轴对称图.

查看试题解析

四、作图题

15. 如图，在正方形网格中，每个小正方形的边长均相等， $△ A B C$ 的三个顶点A，B，C都在格点上．

(1)、在图中画出与 $△ A B C$ 关于直线l成轴对称的 $△ A_{1} B_{1} C_{1}$ ；

(2)、在直线l上找出一点Q，使得 $| Q A + Q C |$ 的值最小；（描出该点并标注字母Q）

(3)、在直线l上找出一点P，使得 $| P A - P C |$ 的值最大．（保留作图痕迹并标注点P）

查看试题解析

五、综合题

16. 如图1，将长方形ABEF的一角向长方形内部折叠，使角的顶点A落在点 $A ′$ 处，OC为折痕，则OC平分 $∠ A O A^{'}$ ．

(1)、若∠AOC＝25°，求 $∠ A O B$ 的度数；

(2)、若点D在线段BE上，角OBD沿着折痕OD折叠落在点 $B ′$ 处，且点 $B ′$ 在长方形内．
①如果点 $B ′$ 刚好在线段 $A^{'} O$ 上，如图2所示，求∠COD的度数；
②如果点 $B ′$ 不在线段 $A^{'} O$ 上，且 $∠ A O B$ ＝40°，求∠AOC+∠BOD的度数．

查看试题解析
17. 如图，∠AOB＝∠EOF＝90°，连接AB．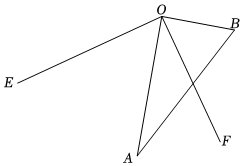

(1)、用尺规作图法在射线OF上作OC＝OB，在射线OE上取点D使CD＝AB；

(2)、连接CD，找一点P使它到四边形OBCD四个顶点的距离之和最小，并说明理由；

(3)、设∠AOF＝α，
①当α＝42°时，求∠BOE的大小；
②当∠AOB绕点O旋转任意角度时，请用α表示∠AOF和∠BOE之间的数量关系，并说明理由．

查看试题解析

2023-2024学年初中数学七年级上册 11.6 轴对称 同步分层训练培优卷(沪教版五四制)

一、选择题

二、填空题

三、解答题

四、作图题

五、综合题

2023-2024学年初中数学七年级上册 11.6 轴对称同步分层训练培优卷(沪教版五四制)