广东省梅州市丰顺县2022-2023学年八年级下学期期末考试数学试题

试卷更新日期：2023-07-28 类型：期末考试

进入出卷网下载

一、选择题:本大题10小题，每小题3分,共30分。

1. 下列图形中既是轴对称图形又是中心对称图形的是（）

A、 B、 C、 D、

查看试题解析
2. 语句“ $x$ 的 $\frac{1}{3}$ 与 $x$ 的和超过2”可以表示为（）

A、 $\frac{x}{3} + x \leq 2$ B、 $\frac{x}{3} + x > 2$ C、 $\frac{x}{3} + x \geq 2$ D、 $\frac{3}{x} + x > 2$

查看试题解析
3. 若分式 $\frac{2}{x - 5}$ 有意义，则x的取值范围是（）

A、 $x > 5$ B、 $x < 5$ C、 $x \neq 5$ D、 $x = 5$

查看试题解析
4. 如图， $△ A B C$ 中， $A B = A C ， ∠ B = 8 0^{°}$ ，则 $∠ A$ 的度数是（）

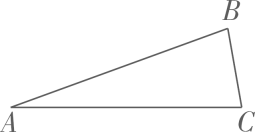A、80° B、70° C、20° D、50°

查看试题解析
5. 若a-b=2，则a²-b²-4b的值是（）

A、0 B、2 C、3 D、4

查看试题解析
6. 为了更好开展劳动教育，实现五育并举，某校开设了劳动实践课程.该校的某劳动实践小组协助公园园区工人测量人工湖湖畔A，B两点之间的距离，该实践小组所画的示意图如图，先在湖边地面上确定点O，再用卷尺分别确定OA，OB的中点C，D，最后用卷尺量出CD=10m，则A，B之间的距离是（）

A、5m B、10m C、15m D、20m

查看试题解析
7. 如图，每个小正方形的边长都是1，A，B，C分别在格点上，则∠ABC的度数为（）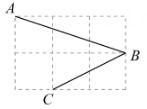

A、30° B、45° C、50° D、60°

查看试题解析
8. 要使如图所示的四边形ABCD是平行四边形，根据图中数据，可以添加的条件是（）

A、OC=5 B、OC=3 C、CD=3 D、CD-9

查看试题解析
9. 数轴上A，B，C三点依次从左向右排列，表示的数分别为-2-x，2x-3和0，则x可能是（）

A、-1 B、0 C、1 D、2

查看试题解析
10. 设 $M = \frac{y + 1}{x + 1} ， N = \frac{y}{x}$ ，当 $x > y > 0$ 时， $M$ 和 $N$ 的大小关系是（）

A、 $M > N$ B、 $M = N$ C、 $M < N$ D、不能确定

查看试题解析

二、填空题:本大题共5小题，每小题3分，共15分。

11. 若a<0，则-a0.(用<，=，>填空)

查看试题解析
12. 计算： $\frac{2 b + a}{a} + \frac{a - 2 b}{a} =$ .

查看试题解析
13. 因式分解： $3 a^{2} - 12 =$ .

查看试题解析
14. 如图，AB-4cm，BC-5cm，AC=2cm，将△ABC沿BC方向平移acm(0<a<5)，得到△DEF，连接AD，则阴影部分的周长为cm.

查看试题解析
15. 如图1，在平面直角坐标系中，.平行四边形ABCD在第一象限，且BC//x轴.直线y=x从原点O出发沿x轴正方向平移.在平移过程中，直线被平行四边形ABCD截得的线段长度m与直线在x轴上平移的距离t的函数图象如图2所示，那么平行四边形ABCD的面积为.

查看试题解析

三、解答题(一):本大题3小题，每小题8分,共24分。

16. 解不等式组 ${\begin{array}{l} 3 x - 2 < 4 \\ 2 (x - 1) \leq 3 x + 1 \end{array}$ ，并求出它的非负整数解．

查看试题解析
17. 解分式方程： $\frac{1}{x - 3} + 3 = \frac{x}{3 - x}$ .

查看试题解析
18. 已知 $a + b = 2 ， a b = - \frac{3}{2}$ .求下列各式的值；

(1)、 $a^{2} b + a b^{2}$ ；

(2)、 $(a - 2) (b - 2)$ .

查看试题解析

四、解答题(二):本大题3小题，每小题9分，共27分。.

19. 如图，在RIOABC中，∠ACB=90°，AC=12，BC=9，AB的垂直平分线分别交AB、AC于点D，E.求CE的长.

查看试题解析
20. 如图所示的正方形网格中，△ABC的顶点均在格点上，请在所给直角坐标系中按要求画图：

(1)、作出△ABC关于坐标原点O成中心对称的△A₁B₁C₁；

(2)、作出以点A旋转中心，将△ABC绕点A顺时针旋转90°得到的△A₂B₂C₂；

(3)、点C₂的坐标为.

查看试题解析
21. 如图，在平行四边形ABCD中，延长BC到点F，使BC=CF，连接AC、DF.

(1)、求证：四边形ACFD是平行四边形。

(2)、若四边形ACFD的面积为7，则四边形ABCD的面积为.

查看试题解析

五、解答题(三):本大题2小题，每小题12分,共24分

22. 自2014年以来，全民阅读连续十年写入政府工作报告，2023年全国教育工作会议进一步提出，要把开展读书活动作为-件大事来抓，引导学生爱读书，读好书，善读书.某校为了提高学生读书兴趣，为各班购买学生读本《三国演义》和《水浒传》若干，其中《三国演义》的单价比《水浒传》的单价贵10元；用5760元购买《水浒传》的数量是用3480元购买《三国演义》数量的2倍.求：

(1)、《水浒传》《三国演义》单价分别是多少元?

(2)、学校准备用不超过10320元的经费，购买这两种书共200本，那么三国演义最多可买多少本?

查看试题解析
23. 如图，在平行四边形ABCD中，AD=2AB=6cm，BE是∠ABC的角平分线，点M从点E出发，沿ED方向以1cm/s的速度向点D运动，点N从点C出发，沿射线CB方向以4cm/s的速度运动，当点M运动到点D时，点N随之停止运动，设运动时间为t(s)，

(1)、求AE的长；

(2)、是否存在以M、E、B、N为顶点的四边形是平行四边形?若存在，求出t的值；若不存在，请说明理由.

(3)、当时，线段NM将平行四边形ABCD面积二等分(直接写出答案)”

查看试题解析