浙江省湖州市德清县2022-2023学年八年级下学期期末调研测试数学试卷

试卷更新日期：2023-07-28 类型：期末考试

进入出卷网下载

一、选择题(本题有10小题，每小题3分，共30分)

1. 在下列图形中，是中心对称图形的是（）

A、 B、 C、 D、

查看试题解析
2. 如图，DE是△ABC的中位线，若BC=8，则DE的长是（）

A、3 B、4 C、5 D、6

查看试题解析
3. 下列运算结果正确的是（）

A、 $\sqrt{3} + \sqrt{2} = \sqrt{5}$ B、 $\sqrt{3} \times \sqrt{2} = \sqrt{5}$ C、 $3 \sqrt{5} - \sqrt{5} = 2$ D、 $\sqrt{18} \div \sqrt{2} = 3$

查看试题解析
4. 在平面直角坐标系xOy中，若点 $A (2 ， y_{1}) ， B (5 ， y_{2})$ 在反比例函数 $y = \frac{k}{x} (k > 0 ， k$ 为常数)的图象上，则（）

A、 $y_{1} > y_{2}$ B、 $y_{1} \geq y_{2}$ C、 $y_{1} = y_{2}$ D、 $y_{1} < y_{2}$

查看试题解析

5. 甲、乙、丙、丁四名射击运动员进行射击测试，每人10次射击成绩的平均数

\bar{x}

(单位：环)及方差

S^{2}

(单位：环

^{2}

)如下表所示：

	甲	乙	丙	丁
$\bar{x}$	9	9	9	9
$S^{2}$	1.6	1.2	3	0.8

根据表中数据，要从中选择一名成绩好且发挥稳定的运动员参加比赛，应选择（）

A、甲 B、乙 C、丙 D、丁

查看试题解析

6. 一元二次方程x²-4x+4=0的根的情况为（）

A、有两个不相等的实数根 B、没有实数根 C、有两个相等的实数根 D、只有一个实数根

查看试题解析
7. 如图，平行四边形ABCD的对角线交于点E，已知AB=5cm，△ABE的周长比△BEC的周长小3cm，则AD的长度为（）

A、8cm B、5cm C、3cm D、2cm

查看试题解析
8. 高空抛物极其危险，是我们必须杜绝的行为，据研究，高空抛物下落的时间1(单位：s)和高度 $h$ (单位： $m$ )近似满足公式 $t = \sqrt{\frac{h}{5}}$ (不考尼风速的影响).记从 $50 m$ 高空抛物到落地所需时间为 $t_{1}$ ，从 $100 m$ 高空抛物到落地所需时间为 $t_{2}$ ，则 $t_{2} ： t_{1}$ 的值是（）

A、 $2 \sqrt{5}$ B、 $\sqrt{5}$ C、 $\sqrt{2}$ D、2

查看试题解析
9. 如图，在平面直角坐标系中，反比例函数 $y = \frac{k}{x} (k > 0 ， x > 0)$ 的图象经过 $△ A O B$ 的顶点 $B$ .若 $A B / / y$ 轴，点 $A$ 的坐标为 $(3 ， 2) ， △ O A B$ 的面积为3，5，则 $k$ 的值为（）

A、6.5 B、7 C、13 D、14

查看试题解析
10. 如图，将两个等腰直角三角形 $△ A E F$ 和 $△ C E F$ 拼接在正方形ABCD内部，其中 $∠ A E F = ∠ E F C = 9 0^{°}$ ，下列结论：①四边形AECF是平行四边形：②△ABF是直角三角形：③若 $A B = \sqrt{10}$ ，则 $A F = 2 \sqrt{2} ，$ 其中正确结论的编号是（）

A、①② B、①③ C、②③ D、①②③

查看试题解析

二、填空题(本有6小题，每小题4分，共24分)

11. 使代数式 $\sqrt{x - 1}$ 有意义的x的取值范围是．

查看试题解析
12. 四边形的内角和是度

查看试题解析
13. 若关于x的一元二次方程x²+ax+2a+3=0的一个根是1，则a的值是.

查看试题解析
14. 如图，E是平行四边形ABCD内一点，△BCE是正三角形，连结AE，DE，若AELAD，DE⊥EC，且AE=1，∠ADE=30"，则AB的长是.

查看试题解析
15. 如图，一次函数 $y = k_{1} x + b$ ( $k_{1}$ 和 $b$ 均为常数且 $k_{1} > 0)$ 与反比例函数 $y = \frac{k_{2}}{x} (k_{2}$ 为常数且 $k_{2} < 0)$ 的图象交于A，B两点，其横坐标分别为1和2.5，则关于 $x$ 的不等式 $\frac{k_{2}}{x} - k_{1} x - b > 0$ 的解集是.

查看试题解析
16. 如图，在平面直角坐标系中，反比例函数 $y = \frac{k}{x} (k > 0 ， k$ 是常数)在第一象限部分的图象与矩形OABC的两边AB和BC分别交于D，F两点，将 $△ O A D$ 沿OD翻折得到 $△ O E D ， D E$ 的延长线恰好经过点 $C$ .若 $∠ E O C = 4 5^{°}$ ，则 $\frac{C F}{B F}$ 的值是.

查看试题解析

三、解答题(本题有8小题，共66分)

17. 计算，

(1)、 $(\sqrt{6})^{2} - \sqrt{(- 2)^{2}}$ .

(2)、 $\sqrt{18} - \sqrt{4} \times \sqrt{2} + \sqrt{\frac{1}{2}}$

查看试题解析
18. 解方程：

(1)、x²-9=0

(2)、x²-6x+1=0

查看试题解析
19. 如图，在6x6的正方形网格中，每个小正方形的边长为1，线段AB的两个端点在网格的格点上，分别按下列要求画格点四边形(顶点均在格点上).

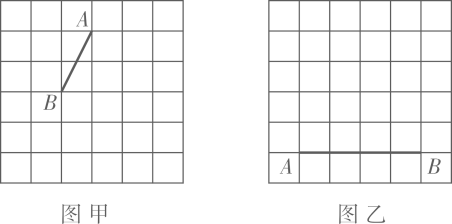(1)、在图甲中画一个菱形ABCD：

(2)、在图乙中画一个平行四边形ABCD，使得平行四边形ABCD的面积为12.

查看试题解析
20. 某校在“书籍授受知识，文明启迪智慧”系列读书活动中，为了解学生参加读
书活动的情况，随机调查了部分学生每人参加活动的项目数量，根据统计的结果，绘制出如下统计图，
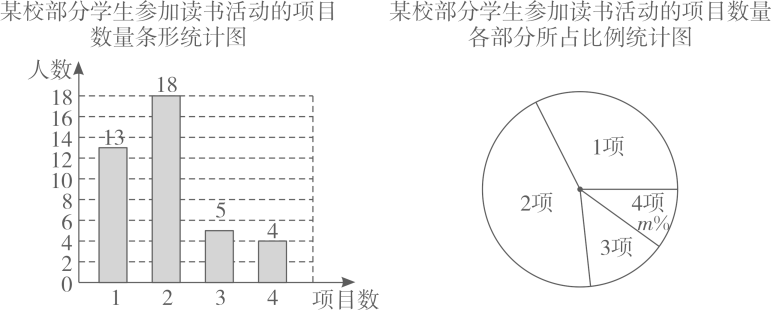
请根据相关信息，解答下列问题：

(1)、本次接受调查的学生人数为人，图中m的值为.

(2)、求被调查学生参加活动的项目数量的平均数和中位数，

查看试题解析
21. 如图，在△ABC中，AB=AC，D为BC的中点，四边形ABDE是平行四边形，AC，DE相交于点O.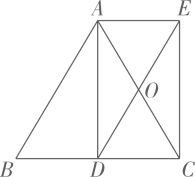

(1)、求证：四边形ADCE是矩形：

(2)、若∠AOE=60°，AE=4，求AD的长.

查看试题解析
22. “杭州亚运●三人制篮球”赛将于9月25-10月1日在我县举行，我县某商店
抓住商机，销售某款篮球服.6月份平均每天售出100件，每件盈利40元.为了扩大销售、增加盈利，7月份该店准备采取降价措施，经过市场调研，发现销售单价每降低1元，平均每天可多售出10件.

(1)、若降价5元，求平均每天的销售数量：

(2)、当每件商品降价多少元时，该商店每天销售利润为6000元?

查看试题解析
23. 如图1，在平面直角坐标系中，反比例函数y= $\frac{k}{x}$ (k>0，k为常数，x>0)的图象经过正方形ABCO的顶点B，点A的坐标是(0，1).点D在线段OA上，点E在射线OC上，以BD，DE为边的平行四边形BDEF的顶点F恰好在该反比例函数的图象上

(1)、求k的值：

(2)、若点D的坐标是(0， $\frac{1}{3}$ )，求点E的坐标：

(3)、如图2，当点E在OC的延长线上时，连结BE若BD⊥BE，BD=BE.求点D的坐标.

查看试题解析
24. 已知菱形ABCD和等边△CEF，∠ABC=60°，

(1)、当E，F分别在CA，CB的延长线上时(如图1)，连结AF，DE.
①求证：AF=DE：
②连结DF，交AB于点N(如图2)，取AE的中点M，连结MN.若AE=AC=3，求MN的长：

(2)、当点F在DA的延长线上时(如图3)，连结AE，DE，分别取AE，DF的中点M，N，连结MN.若AC=2，CE= $\sqrt{19}$ ，求MN的长，

查看试题解析