广东省肇庆市封开县2022-2023学年八年级下册数学期末试卷
试卷更新日期:2023-07-28 类型:期末考试
一、选择题(本大题10小题,每小题3分,共30分)在每小题列出的四个选项中,只有一个是正确的,请把正确选项涂在答题卡上.
-
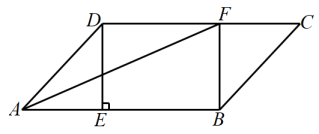
1. 下列二次根式中,最简二次根式是( ).A、 B、 C、 D、2. 下列计算正确的是( )A、 B、 C、 D、3. 小华想用老师提供的三条线段首尾相连围成一个直角三角形,则他应该选择的三条线段长度是( )A、、、 B、、、 C、、、 D、、、4. 如图,在四边形 中, ,要使四边形 是平行四边形,下列添加的条件不正确的是( )
 A、 B、 C、 D、5. 函数的图像经过点 , 则的值为( )A、1 B、 C、 D、6. 2022年北京冬奥会自由式滑雪女子U型场地技巧决赛中,中国金牌选手谷爱凌第二跳分数如下:95,95,95,95,96,96,关于这组数据,下列描述正确的是( )A、中位数是95 B、众数是95.5 C、平均数是95.25 D、方差是0.017. 下列命题中,错误的是( )A、有两个角相等的梯形是等腰梯形 B、顺次联结矩形各边中点所成四边形是菱形 C、对角线相等的平行四边形是矩形 D、对角线互相平分且相等的四边形是矩形8. 如图,在中, , , 按以下步骤作图:第一步,一点为圆心,适当的长为半径作弧,分别交 , 于、两点;第二步,分别以点、为圆心,大于的长为半径作弧,两弧相交于点;第三步,作射线 , 交于点 . 则的长为( )
A、 B、 C、 D、5. 函数的图像经过点 , 则的值为( )A、1 B、 C、 D、6. 2022年北京冬奥会自由式滑雪女子U型场地技巧决赛中,中国金牌选手谷爱凌第二跳分数如下:95,95,95,95,96,96,关于这组数据,下列描述正确的是( )A、中位数是95 B、众数是95.5 C、平均数是95.25 D、方差是0.017. 下列命题中,错误的是( )A、有两个角相等的梯形是等腰梯形 B、顺次联结矩形各边中点所成四边形是菱形 C、对角线相等的平行四边形是矩形 D、对角线互相平分且相等的四边形是矩形8. 如图,在中, , , 按以下步骤作图:第一步,一点为圆心,适当的长为半径作弧,分别交 , 于、两点;第二步,分别以点、为圆心,大于的长为半径作弧,两弧相交于点;第三步,作射线 , 交于点 . 则的长为( )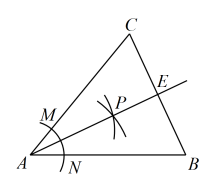 A、 B、8 C、 D、109. 关于函数的图象,如下说法中正确的有( )
A、 B、8 C、 D、109. 关于函数的图象,如下说法中正确的有( )①图象过点;②图象与轴的交点是;③由图象可知随的增大而增大;④图象不经过第一象限.
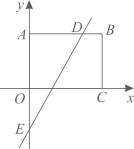
A、4个 B、3个 C、2个 D、1个10. 已知一次函数和 , 则函数和的图象可能是( )A、 B、
B、 C、
C、 D、
D、
二、填空题(本大题5小题,每小题3分,共15分)请将下列各题的正确答案填写在答题卡相应的位置上.
-
11. 化简: .12. 若 在实数范围内有意义,则实数x的取值范围是 .13. 如图所示,一场暴雨过后,垂直于地面的一棵树在距地面3米的处折断,树尖恰好碰到地面,经测量米,折断前树高为米.
 14. 已知一次函数的图像经过点 , 且函数的值随的增大而减小,则k的值为 .15. 如图1,菱形纸片的边长为 , , 将菱形沿 , 折叠,使得点 , 两点重合于对角线上的点(如图2).若 , 则六边形的面积为 .
14. 已知一次函数的图像经过点 , 且函数的值随的增大而减小,则k的值为 .15. 如图1,菱形纸片的边长为 , , 将菱形沿 , 折叠,使得点 , 两点重合于对角线上的点(如图2).若 , 则六边形的面积为 .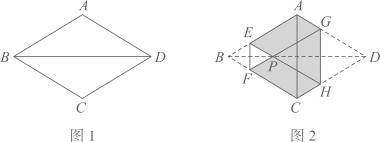
三、解答题(一)(本大题3小题,每小题8分,共24分)
-
16. 计算: .17. 如图,在四边形中, , 点、在上, , 且 . 求证:四边形是平行四边形.
 18. 已知与成正比例,且当时, .(1)、求与的函数关系式;(2)、把正比例函数的图像向上平移3个单位得到函数的图像,与轴交于点 , 与轴交于点 , 写出函数关系式,并求出、的坐标.
18. 已知与成正比例,且当时, .(1)、求与的函数关系式;(2)、把正比例函数的图像向上平移3个单位得到函数的图像,与轴交于点 , 与轴交于点 , 写出函数关系式,并求出、的坐标.四、解答题(二)(本大题3小题,每小题9分,共27分)
-
19. 2021年4月2日,教育部发布《关于进一步加强中小学生睡眠管理工作的通知》,明确了学生睡眠时间要求,其中,初中生每天睡眠时间应达到9小时.某校为了了解初中学生每天的睡眠时间是否达到要求,随机调查了该校的部分初中学生每天的睡眠时间,根据调查结果绘制出如图不完整的统计图.请根据相关信息,解答下列问题:
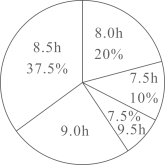
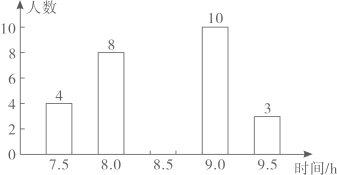 (1)、填空:扇形统计图中,“”对应的扇形圆心角的度数 , 所调查的初中学生每天睡眠时间的众数是 , 中位数是;(2)、求所调查的初中学生每天的平均睡眠时间;(3)、若该校有1600名初中学生,睡眠时间小于9小时的学生要参加相关科普讲座,请你估计该校有多少初中学生要参加科普讲座?20. 如图,D为边上的一点, , , , , 求的长.
(1)、填空:扇形统计图中,“”对应的扇形圆心角的度数 , 所调查的初中学生每天睡眠时间的众数是 , 中位数是;(2)、求所调查的初中学生每天的平均睡眠时间;(3)、若该校有1600名初中学生,睡眠时间小于9小时的学生要参加相关科普讲座,请你估计该校有多少初中学生要参加科普讲座?20. 如图,D为边上的一点, , , , , 求的长. 21. 如图,正比例函数的图像与一次函数的图像交于点 , 一次函数图象经过点 , 与轴的交点为 , 与轴的交点为 .
21. 如图,正比例函数的图像与一次函数的图像交于点 , 一次函数图象经过点 , 与轴的交点为 , 与轴的交点为 .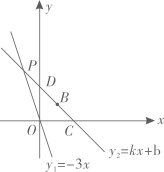 (1)、求一次函数表达式;(2)、求的面积;(3)、写出当时,的取值范围.
(1)、求一次函数表达式;(2)、求的面积;(3)、写出当时,的取值范围.五、解答题(三)(本大题2小题,每小题12分,共24分)