陕西省西安市高新重点中学2022-2023学年八年级下册数学期末试卷
试卷更新日期:2023-07-28 类型:期末考试
一、选择题(本大题共10小题,共30.0分。在每小题列出的选项中,选出符合题目的一项)
-
1. 下列图形中,既是轴对称图形又是中心对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 2. 如果 , 下列各式中正确的是( )A、 B、 C、 D、3. 平行四边形的对角线( )A、长度相等 B、互相平分 C、互相垂直 D、以上都对4. 下面式子从左边到右边的变形是因式分解的是( )A、 B、 C、 D、5. 在如图右侧的四个三角形中,不能由经过旋转或平移得到的是( )
2. 如果 , 下列各式中正确的是( )A、 B、 C、 D、3. 平行四边形的对角线( )A、长度相等 B、互相平分 C、互相垂直 D、以上都对4. 下面式子从左边到右边的变形是因式分解的是( )A、 B、 C、 D、5. 在如图右侧的四个三角形中,不能由经过旋转或平移得到的是( ) A、 B、 C、 D、6. 如图,直线与且 , 为常数的交点坐标为 , 则关于的不等式的解集为( )
A、 B、 C、 D、6. 如图,直线与且 , 为常数的交点坐标为 , 则关于的不等式的解集为( ) A、 B、 C、 D、7. 千里江山图是宋代王希孟的作品,如图,它的局部画面装裱前是一个长为米,宽为米的矩形,装裱后,整幅图画宽与长的比是: , 且四周边衬的宽度相等,则边衬的宽度应是多少米?设边衬的宽度为米,根据题意可列方程( )
A、 B、 C、 D、7. 千里江山图是宋代王希孟的作品,如图,它的局部画面装裱前是一个长为米,宽为米的矩形,装裱后,整幅图画宽与长的比是: , 且四周边衬的宽度相等,则边衬的宽度应是多少米?设边衬的宽度为米,根据题意可列方程( ) A、 B、 C、 D、8. 若关于x的方程 = 无解,则m的值为( )A、0 B、4或6 C、6 D、0或49. 如图,等边的顶点 , , 规定把“先沿轴翻折,再向右平移1个单位”为一次变换,这样连续经过2022次变换后,等边的顶点的坐标为( )
A、 B、 C、 D、8. 若关于x的方程 = 无解,则m的值为( )A、0 B、4或6 C、6 D、0或49. 如图,等边的顶点 , , 规定把“先沿轴翻折,再向右平移1个单位”为一次变换,这样连续经过2022次变换后,等边的顶点的坐标为( ) A、 B、 C、 D、10. 如图,等边 边长为a,点O是 的内心, ,绕点O旋转 ,分别交线段AB,BC于D,E两点,连接DE,给出下列四个结论:① 形状不变;② 的面积最小不会小于四边形 的面积的四分之一;③四边形 的面积始终不变;④ 周长的最小值为1.5a.上述结论中正确的个数是( )
A、 B、 C、 D、10. 如图,等边 边长为a,点O是 的内心, ,绕点O旋转 ,分别交线段AB,BC于D,E两点,连接DE,给出下列四个结论:① 形状不变;② 的面积最小不会小于四边形 的面积的四分之一;③四边形 的面积始终不变;④ 周长的最小值为1.5a.上述结论中正确的个数是( )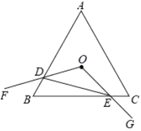 A、4 B、3 C、2 D、1
A、4 B、3 C、2 D、1二、填空题(本大题共6小题,共18.0分)
-
11. 分式 的值为 ,则 的值为.12. 已知一个正多边形的一个内角是其相邻外角的倍,则该该边形的边数是 .13. 如图,在中,是边的中点,过点作平分线的垂线,垂足为 , 连接 , 若 , , 则 .
 14. 若关于的不等式有且只有四个整数解,且一次函数的图象不经过第三象限,则符合题意的整数的值为 .15. 如图,四边形中, , , , 是的中点,点以每秒个单位长度的速度从点出发,沿向点运动;点同时以每秒个单位长度的速度从点出发,沿向点运动,点停止运动时,点也随之停止运动.当运动时间秒时,以点 , , , 为顶点的四边形是平行四边形.
14. 若关于的不等式有且只有四个整数解,且一次函数的图象不经过第三象限,则符合题意的整数的值为 .15. 如图,四边形中, , , , 是的中点,点以每秒个单位长度的速度从点出发,沿向点运动;点同时以每秒个单位长度的速度从点出发,沿向点运动,点停止运动时,点也随之停止运动.当运动时间秒时,以点 , , , 为顶点的四边形是平行四边形. 16. 如图等边中, , 为的中点,为内一动点, , 连接 , 将线段绕点顺时针旋转得 , 连接 , 则线段最小值为 .
16. 如图等边中, , 为的中点,为内一动点, , 连接 , 将线段绕点顺时针旋转得 , 连接 , 则线段最小值为 .
三、解答题(本大题共9小题,共72.0分。解答应写出文字说明,证明过程或演算步骤)
-
17.(1)、分解因式; .(2)、解不等式组: .18.(1)、解方程 ,(2)、 , 从、、、几个数中选取一个作为的值代入.19. 如图,已知平行四边形 , 将这个四边形折叠,使得点和点重合,请你用尺规作出折痕所在的直线.保留作图痕迹,不写作法
 20. 如图,在平面直角坐标系中,的顶点分别为 , , .
20. 如图,在平面直角坐标系中,的顶点分别为 , , .
⑴在图中画出将先向下平移个单位长度,再向右平移个单位长度得到的 , 点、、的对应点分别为、、;
⑵以点为对称中心,在图中画出与成中心对称的 , 点、、的对应点分别为、、 , 并写出点的坐标.
21. 某单位计划从商店购买同一种品牌的钢笔和笔记本,已知购买一支钢笔比购买一个笔记本多用20元,若用1500元购买钢笔和用600元购买笔记本,则购买钢笔的数量是购买笔记本数量的一半.(1)、求购买一支钢笔、一个笔记本各需要多少元?(2)、经商谈,商店给予优惠,优惠方式是每购买一支钢笔赠送一个笔记本;如果此单位需要笔记本的数量是钢笔数量的3倍还少6个,且购买钢笔和笔记本的总费用不超过1020元,那么最多可购买多少支钢笔?22. 如图,在中,是边上任意一点,是的中点,连接 , 过点作交的延长线于点 , 连接 , . (1)、求证:四边形是平行四边形;(2)、若 , , , 求的长.23. 阅读理解:已知 , , 试比较与的大小.
(1)、求证:四边形是平行四边形;(2)、若 , , , 求的长.23. 阅读理解:已知 , , 试比较与的大小.想法:求当 , 则;当 , 则;当 , 则 .
解: , .
用你学到的方法解决下列问题:
(1)、已知且 , , 试比较与的大小.(2)、甲、乙两地相距 , 小明和小宇同路往返于甲乙两地.小明去时和返回时的速度分别是、 , ;小宇去时和返回时的速度都是请问二者一个来回中,谁用时更短?24. 如图1,点C、D是线段AB同侧两点,且AC=BD,∠CAB=∠DBA,连接BC,AD交于点E. (1)、求证:AE=BE;(2)、如图2,△ABF与△ABD关于直线AB对称,连接EF.
(1)、求证:AE=BE;(2)、如图2,△ABF与△ABD关于直线AB对称,连接EF.①判断四边形ACBF的形状,并说明理由;
②若∠DAB=30°,AE=5,DE=3,求线段EF的长.
25.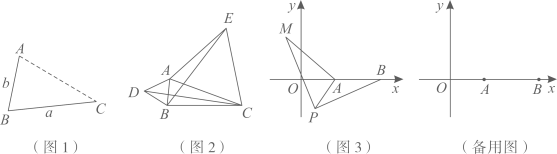 (1)、发现:如图 , 点为线段外一动点,且 , .
(1)、发现:如图 , 点为线段外一动点,且 , .填空:当点位于时,线段的长取得最大值,且最大值为用含 , 的式子表示
(2)、应用:点为线段外一动点,且 , , 如图所示,分别以 , 为边,作等边三角形和等边三角形 , 连接 , .①请找出图中与相等的线段,并说明理由;
②直接写出线段长的最大值.
(3)、拓展:如图 , 在平面直角坐标系中,点的坐标为 , 点的坐标为 , 点为线段外一动点,且 , , , 请直接写出线段长的最大值及此时点的坐标.