陕西省西安市鄠邑区2022-2023学年八年级下册数学期末试卷
试卷更新日期:2023-07-28 类型:期末考试
一、选择题(本大题共8小题,共24.0分。在每小题列出的选项中,选出符合题目的一项)
-
1. 下列绿色能源图标中既是轴对称图形又是中心对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 2. 若分式的值为 , 则的值为( )A、 B、 C、 D、3. 若 , 则下列不等式中正确的是( )A、 B、 C、 D、4. 如图,在中, , , 是腰上的高,则的长( )
2. 若分式的值为 , 则的值为( )A、 B、 C、 D、3. 若 , 则下列不等式中正确的是( )A、 B、 C、 D、4. 如图,在中, , , 是腰上的高,则的长( )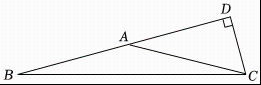 A、 B、 C、 D、5. 下列因式分解正确的是( )A、 B、 C、 D、6. 如图,直线和直线相交于点 . 则不等式组的解集为( )
A、 B、 C、 D、5. 下列因式分解正确的是( )A、 B、 C、 D、6. 如图,直线和直线相交于点 . 则不等式组的解集为( )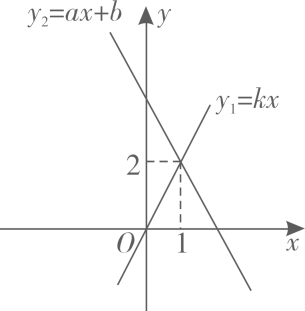 A、 B、 C、 D、或7. 如图,是平行四边形对角线的交点,过的直线分别交、 , 下列结论不正确的是( )
A、 B、 C、 D、或7. 如图,是平行四边形对角线的交点,过的直线分别交、 , 下列结论不正确的是( )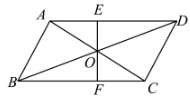 A、 B、 C、 D、四边形和的面积相等8. 如图,已知中, , , 将绕点逆时针旋转得到 , 以下结论: , , , , 正确的有( )
A、 B、 C、 D、四边形和的面积相等8. 如图,已知中, , , 将绕点逆时针旋转得到 , 以下结论: , , , , 正确的有( )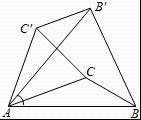 A、 B、 C、 D、
A、 B、 C、 D、二、填空题(本大题共5小题,共15.0分)
-
9. 已知点与点关于原点对称,则 .10. 一个多边形的内角和与外角和的和是720°,那么这个多边形的边数 .11. 如果关于的方程有增根,那么的值是 .12. 如图,将Rt沿着点到的方向平移到的位置,此时 , , 阴影部分面积为40,则平移的距离为 .
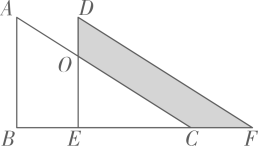 13. 如图,等边中, , 、分别是AB,AC的中点,延长BC到点 , 使 , 连接DE,CD,EF.则四边形的周长是 .
13. 如图,等边中, , 、分别是AB,AC的中点,延长BC到点 , 使 , 连接DE,CD,EF.则四边形的周长是 .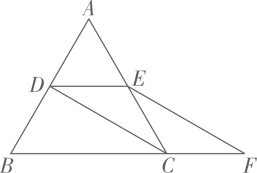
三、计算题(本大题共2小题,共10.0分)
-
14. 化简 .15. 解方程: .
四、解答题(本大题共11小题,共71.0分。解答应写出文字说明,证明过程或演算步骤)
-
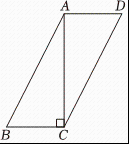
16. 分解因式:(1)、(2)、17. 如图,在▱中, , , , 求▱的面积.
 18. 如图,已知 , 为边上一点,请用尺规作图的方法在边上求作一点 , 使保留作图痕迹,不写作法
18. 如图,已知 , 为边上一点,请用尺规作图的方法在边上求作一点 , 使保留作图痕迹,不写作法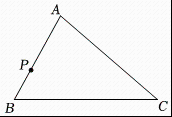 19. 如图,已知在中,是的垂直平分线,垂足为 , 交于点 , 若 , , 求的周长.
19. 如图,已知在中,是的垂直平分线,垂足为 , 交于点 , 若 , , 求的周长.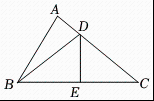 20. 如图,线段、相交于点 , 连接、 , 已知 , 求证: .
20. 如图,线段、相交于点 , 连接、 , 已知 , 求证: .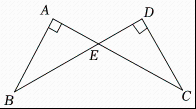 21. 解不等式组 , 并将其解集在数轴上表示出来.
21. 解不等式组 , 并将其解集在数轴上表示出来.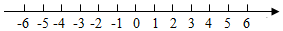 22. 如图,是的角平分线, , 交于点 .
22. 如图,是的角平分线, , 交于点 .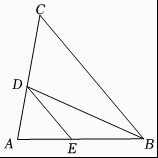 (1)、求证: .(2)、当时,请判断与的大小关系,并说明理由.23. 先化简,再求值: , 从 , , 中选择合适的的值代入求值.24. 如图,在四边形中,与交于点 , , , 垂足分别为点 , , 且 , 求证:四边形是平行四边形.
(1)、求证: .(2)、当时,请判断与的大小关系,并说明理由.23. 先化简,再求值: , 从 , , 中选择合适的的值代入求值.24. 如图,在四边形中,与交于点 , , , 垂足分别为点 , , 且 , 求证:四边形是平行四边形.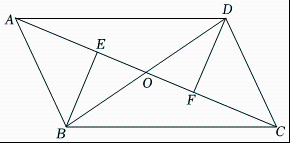 25. 金师傅近期准备换车,看中了价格相同的两款国产车.
25. 金师傅近期准备换车,看中了价格相同的两款国产车.燃油车
油箱容积:升
油价:元升
续航里程:千米
每千米行驶费用:元
新能源车
电池电量:千瓦时
电价:元千瓦时
续航里程:千米
每千米行驶费用:____元
(1)、用含的代数式表示新能源车的每千米行驶费用.(2)、若燃油车的每千米行驶费用比新能源车多元.①分别求出这两款车的每千米行驶费用.
②若燃油车和新能源车每年的其它费用分别为元和元.问:每年行驶里程为多少千米时,买新能源车的年费用更低?年费用年行驶费用年其它费用
26.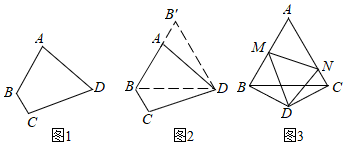
【问题提出】如图 , 在四边形中, , , , , , 求四边形的面积.
【尝试解决】旋转是一种重要的图形变换,当图形中有一组邻边相等时,往往可以通过旋转解决问题.
(1)、如图2,连接 , 由于 , 所以可将绕点顺时针方向旋转 , 得到 , 则的形状是 .(2)、在(1)的基础上,求四边形的面积.(3)、【类比应用】如图 , 等边的边长为 , 是顶角为的等腰三角形,以D为顶点作一个的角,角的两边分别交于点 , 交于点 , 连接 , 求的周长.