福建省泉州市2022-2023学年八年级下册数学期末试卷

试卷更新日期：2023-07-28 类型：期末考试

进入出卷网下载

一、选择题：（共10题，40分）

1. 在式子 $\frac{a - b}{2}$ ， $\frac{2}{5}$ ， $\frac{a - b}{a + 2 b}$ ， $\frac{3}{m}$ 中，分式有（）

A、1个 B、2个 C、3个 D、4个

查看试题解析
2. 人体内的某种球状细胞的直径为 $0.00000156 m$ ，数据0.00000156用科学记数法可表示为（）

A、 $1.56 \times 1 0^{- 6}$ B、 $1.56 \times 1 0^{- 5}$ C、 $156 \times 1 0^{- 5}$ D、 $1.56 \times 1 0^{6}$

查看试题解析
3. 平面直角坐标系中，点 $M$ 在 $x$ 轴的负半轴上，且到原点的距离为4，则点 $M$ 的坐标为（）

A、 $(4 ， 0)$ B、 $(0 ， 4)$ C、 $(- 4 ， 0)$ D、 $(0 ， - 4)$

查看试题解析
4. 下列命题是真命题的是（）

A、对角线相等的四边形是平行四边形 B、对角线互相垂直平分的四边形是正方形 C、对角线互相垂直的四边形是菱形 D、对角线互相平分且相等的四边形是矩形

查看试题解析
5. 某校九年级进行了3次数学模拟考试，甲、乙、丙三名同学的平均分及方差 $s^{2}$ 如表所示，那么这三名同学数学成绩最稳定的是（）

甲

乙

丙

$\bar{x}$

91

91

91

$s^{2}$

6

14

25

A、甲 B、乙 C、丙 D、无法确定

查看试题解析
6. 下列代数式变形正确的是（）

A、 $\frac{- x + y}{4} = - \frac{x + y}{4}$ B、 $\frac{x}{y} = \frac{x z}{y z}$ C、 $\frac{x^{2} - y^{2}}{{(x - y)}^{2}} = \frac{x + y}{x - y}$ D、 $\frac{0.2 x + y}{0.2} = \frac{2 x + y}{2}$

查看试题解析
7. 如图，点A在反比例函数 $y = \frac{k}{x} (x < 0)$ 的图象上， $A B ⊥ x$ 轴于点B，C是OB的中点，连接AO，AC，若△AOC的面积为3，则k的值为（）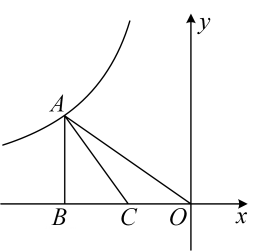

A、12 B、 $- 12$ C、6 D、 $- 6$

查看试题解析
8. 如图，在菱形ABCD中， $∠ A D C = 7 2^{o}$ ， AD的垂直平分线交对角线BD于点P，垂足为E，连接CP，则∠CPB的度数是（）

A、72° B、90° C、100° D、108°

查看试题解析
9. 若不等式 $a x + b > 0$ 的解集是 $x < 3$ ，则下列各点可能在一次函数 $y = a x + b$ 的图象上的是（）

A、 $(- 2 ， - 3)$ B、 $(4 ， 5)$ C、 $(1 ， - 2)$ D、 $(2 ， 2)$

查看试题解析
10. 如图，正方形ABCD中，点E、F、H分别是AB、BC、CD的中点，CE、DF交于点G，连接AG、HG，下列结论：
① $C E ⊥ D F$ ② $H G = \frac{1}{2} B C$ ③△ADG是等边三角形④∠CHG＝∠DAG.
正确的有（）个.

A、1 B、2 C、3 D、4

查看试题解析

	甲	乙	丙
$\bar{x}$	91	91	91
$s^{2}$	6	14	25

二、填空题：（共6题，24分）

11. 在函数 $y = \frac{1}{\sqrt{x + 1}}$ 中，自变量 $x$ 的取值范围是.

查看试题解析
12. 已知平行四边形 $A B C D$ 中， $∠ A + ∠ C = 24 0^{o}$ ，则 $∠ B$ 的度数是．

查看试题解析
13. 若分式方程 $\frac{x}{x - 3} + 1 = \frac{m}{x - 3}$ 有增根，则 $m =$ ．

查看试题解析
14. 如图，已知函数 $y = 2 x + b$ 与函数 $y = k x - 3$ 的图象交于点 $P$ ，则方程组 ${\begin{array}{l} 2 x - y = - b \\ k x - y = 3 \end{array}$ 的解是．

查看试题解析
15. 如图.边长为1的两个正方形互相重合，按住其中一个不动，将另一个绕顶点A顺时针旋转45°，则这两个正方形重叠部分的面积是.

查看试题解析
16. 如图，在矩形ABCD中，AB=4，BC=6，E为BC的中点，若P、Q为BC边上的动点且PQ=1，则AP=的最小值为．

查看试题解析

三、解答题：（86分）

17. 计算： $\sqrt{16} + | 1 - \sqrt{2} | - {(\frac{1}{6})}^{- 1} + {(π - 2023)}^{0}$

查看试题解析
18. 先化简，再求值： $(m + 2 - \frac{5}{m - 2}) \div \frac{m - 3}{m - 2}$ ，其中 $m = \sqrt{5} - 3$

查看试题解析
19. 如图，在平行四边形 $A B C D$ 中，点E、F分别在边 $B C$ 和 $A D$ 上，且 $B E = D F$ ．求证： $A E ∥ C F$

查看试题解析

20. 某学校食堂推行午餐套餐制，现随机抽取中午在学校食堂用餐的20名学生，收集到他们午餐消费金额（单位：元）的数据，并对数据进行整理、描述和分析。下面给出部分信息：

a、这20名学生午餐消费金额数据如下：

4 8 10 9 9 6 9 6 8 8

7 8 8 6 7 9 10 7 8 5

b、这20名学生午餐消费金额数据的频数分布表：

消费金额	$4 \leq x < 6$	$6 \leq x < 8$	$8 \leq x < 10$	$10 \leq x < 12$
频数	2	6	m	2

c、这20名学生午餐消费金额数据的平均数、中位数、众数

	平均数	中位数	众数
7.6	n	t

(1)、写出表中m、n、t的值

(2)、为了合理膳食结构，学校食堂推出A、B、C三种不同价格不同的套餐，据调查，午餐消费金额在的学生中有50%选择B套餐，用餐消费金额在的学生中有60%选择B套餐，其余学生选择A套餐或C套餐。若每天中午约有800名的学生在食堂用餐，估计食堂每天中午需准备B套餐的份数。

查看试题解析

21. 某容器有一根进水管和一根出水管，进水管和出水管的速度都是恒定的。从某一时刻开始计时，前5分钟内只打开进水管，在第5分钟时，又打开出水管，第13分钟时关掉两根水管。容器内的水量 $y$ （单位：L）与时间 $x$ （单位： $m i n$ ）之间的关系如图所示：

(1)、当 $0 \leq x \leq 5$ 时，求 $y$ 与 $x$ 的关系式。

(2)、求出水管的出水速度。

查看试题解析
22. 如图，将矩形 $A B C D$ 折叠，使A、C重合，折痕分别与 $A D$ 、 $B C$ 相交于E、F，连接 $A F$ ， $C E$ ．

(1)、求证：四边形AFCE是菱形．

(2)、若矩形ABCD的边 $A B = 6$ ， $B C = 8$ ，求线段 $E F$ 的长度。

查看试题解析
23. 为了全面贯彻党的教育方针，保障学生在校1小时体育活动时间。某班计划采购A、B两种型号的跳绳。已知每条B种跳绳的价格比每条A种跳绳的价格多10元。用750元购买A种跳绳与用1250元购买B种跳绳的数量相等。

(1)、求每条A、B两种跳绳的价格各多少元？

(2)、若要购进A、B两种跳绳共50条，且B种跳绳不少于A种跳绳数量的2倍，求购买这两种跳绳总费用的最小值。

查看试题解析
24. 如图，△AOB和△COD均为等腰直角三角形，点O为直角顶点，连接AD，BC，点E是线段BC的中点，连接OE．

(1)、【问题解决】
如图①，当 $C$ ， $D$ 两点分别在边 $O A$ ， $O B$ 上时，线段 $E O$ 与线段 $A D$ 之间的数量关系为

(2)、【类比探究】
将△COD绕点O顺时针旋转到如图②所示位置，请探究（1）中的数量关系是否成立，并说明理由．

(3)、【拓展延伸】
在 $△ C O D$ 的旋转过程中，当 $∠ A O C = 15 0^{o}$ 时， $O A = 6$ ， $O C = 2$ ，请直接写出 $O E$ 的长．

查看试题解析
25. 如图1，在平面直角坐标系中，点 $A (- 2 ， 0)$ ，点 $B (0 ， 2)$ ，直线 $A B$ 与反比例函数 $y = \frac{k}{x} (x > 0)$ 的图象在第一象限交于点 $C (a ， 4)$ ．

(1)、求反比例函数的解析式

(2)、如图2，点 $E (4 ， m)$ 是反比例函数 $y = \frac{k}{x} (x > 0)$ 图象上一点，连接 $C E$ ， $A E$ 。试问在 $x$ 轴上是否存在一点 $D$ ，使△ACD的面积与△ACE的面积相等，若存在，请求出点 $D$ 的坐标；若不存在，请说明理由。

(3)、在（2）的条件下，坐标原点O关于点 $D$ 的对称点为 $G$ ，且点 $G$ 在 $x$ 轴的正半轴上，若点 $M$ 是反比例函数的第一象限图象上一个动点，连接MG，以MG为边作正方形 $M G N F$ ，当顶点 $F$ 恰好落在直线 $A B$ 上时，求点M的坐标。

查看试题解析