广东省韶关市翁源县2022-2023学年九年级上学期期末数学试题

试卷更新日期：2023-07-28 类型：期末考试

进入出卷网下载

一、选择题（每小题3分，共30分）

1. 下列各图中，不是中心对称图形的是（）

A、①③ B、②④ C、②③ D、①④

查看试题解析
2. 一元二次方程 $x^{2} - 6 x - 5 = 0$ 配方后可变形为（）

A、 ${(x - 3)}^{2} = 14$ B、 ${(x - 3)}^{2} = 4$ C、 ${(x + 3)}^{2} = 14$ D、 ${(x + 3)}^{2} = 4$

查看试题解析
3. 方程 $2 x^{2} - 5 x + 3 = 0$ 的根的情况是（）

A、有两个相等的实数根 B、有两个不相等的实数根 C、没有实数根 D、只有一个实数根

查看试题解析
4. 小兰画了一个函数 $y = x^{2} + a x + b$ 的图象如图，关于 $x$ 的方程 $x^{2} + a x + b = 0$ 的解是（）

A、无解 B、 $x = 1$ C、 $x = - 4$ D、 $x = - 1$ 或 $x = 4$

查看试题解析
5. 在平面直角坐标系 $x O y$ 中，点 $A (- 1 ， 2)$ 关于原点对称的点的坐标是（）

A、 $(1 ， - 2)$ B、 $(- 1 ， 2)$ C、 $(- 2 ， 1)$ D、 $(- 1 ， - 2)$

查看试题解析
6. 如图所示，四边形 $A B C D$ 为 $⊙ O$ 的内接四边形， $∠ B C D = 130 °$ ，则 $∠ B O D$ 的大小是（）

A、120° B、110° C、100° D、50°

查看试题解析
7. 如图， $A B$ 是 $⊙ O$ 的直径， $∠ D = 32 °$ ，则 $∠ B O C$ 等于（）

A、32° B、58° C、60° D、64°

查看试题解析
8. 下列事件中，是随机事件的是（）

A、明天下雨 B、15个人中至少有两个人出生在同月 C、三角形内角和为180° D、太阳从西方升起

查看试题解析
9. 不透明的袋中装有只有颜色不同的10个小球，其中6个红色，4个白色，从袋中任意摸出一个球是红球的概率是（）．

A、 $\frac{2}{3}$ B、 $\frac{3}{5}$ C、 $\frac{1}{2}$ D、 $\frac{2}{5}$

查看试题解析
10. 如图，抛物线 $y = a x^{2} + b x + c$ 的对称轴为直线 $x = 1$ ，经过点 $(3 ， 0)$ ．下列结论：① $a b c > 0$ ；② $b^{2} - 4 a c > 0$ ；③ $3 a + c = 0$ ；④抛物线经过点 $(- 3 ， y_{1})$ 和 $(4 ， y_{2})$ ，则 $y_{1} > y_{2}$ ；⑤ $a m^{2} - b ≤ a - b m$ （ $m$ 为任意实数）．其中，正确结论的个数是（）

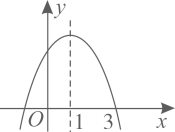A、1 B、2 C、3 D、4

查看试题解析

二、填空题（每小题3分，共15分）

11. 若关于 $x$ 的方程 $x^{2} - k x - 12 = 0$ 的一个根为2，则 $k$ 的值为．

查看试题解析
12. 如果点 $M (- 2 ， y_{1})$ ， $N (- 1 ， y_{2})$ 在二次函数 $y = - x^{2} + 2 x$ 的图象上，则 $y_{1}$ $y_{2}$ （填“＞”、“＜”或“＝”）

查看试题解析
13. 已知圆锥的底面半径是3cm，母线长为6cm，侧面积为 $c m^{2}$ ．

查看试题解析
14. 如图，小明的健康绿码示意图，用黑白打印机打印于边长为10cm的正方形区域内，为了估计图中黑色部分的总面积，在正方形区域内随机掷点，经过大量重复试验，发现点落入黑色部分的频率稳定在0.6左右，据此可以估计黑色部分的总面积约为 $c m^{2}$ ．

查看试题解析
15. 如图，正 $Δ A B O$ 的边长为4， $O$ 为坐标原点，A在 $x$ 轴上， $Δ A B O$ 沿 $x$ 轴正方向作无滑动的翻滚，经一次翻滚后得到 $Δ A_{1} B_{1} O$ ，翻滚2022次后 $A B$ 中点 $M$ 坐标为．

查看试题解析

三、解答题（一）（每小题8分，共24分）

16. 解方程： $x^{2} - 8 x - 9 = 0$ ．

查看试题解析
17. 抛物线的顶点坐标为 $(3 ， - 1)$ 且经过点 $(2 ， 3)$ ，求该抛物线解析式．

查看试题解析
18. 不透明的口袋里装有白、红、黄三种颜色的乒乓球（除颜色外其余都相同），其中白球有2个，红球有1个，现从中任意摸出一个是白球的概率为 $\frac{1}{2}$ ．

(1)、袋中黄球的个数为．

(2)、第一次任意摸一个球（不放回），第二次再摸一个球，请用画树状图或列表格法，求两次摸到都是白球的概率．

查看试题解析

四、解答题（二）（每小题9分，共27分）

19. 如图，在平面直角坐标系中， $Δ A B C$ 三个顶点的坐标分别为 $A (2 ， 4)$ ， $B (1 ， 1)$ ， $C (4 ， 3)$ ．

⑴请画出 $Δ A B C$ 关于原点对称的 $Δ A_{1} B_{1} C_{1}$ ；

⑵请画出 $Δ A B C$ 绕点 $B$ 逆时针旋转90°后的 $Δ A_{2} B_{2} C_{2}$ ，求点 $A$ 到 $A_{2}$ 所经过的路径长．

查看试题解析
20. 如图， $A B$ 是 $⊙ O$ 的直径， $C D$ 是 $⊙ O$ 的一条弦，且 $C D ⊥ A B$ 于 $E$ ，连接 $A C$ ， $O C$ ， $B C$ ．

(1)、求证： $∠ 1 = ∠ 2$ ；

(2)、若 $B E = 2$ ， $C D = 6$ ，求 $⊙ O$ 的半径的长．

查看试题解析
21. 某校计划利用一片空地建一个学生自行车车棚，其中一面靠墙，墙的最大可用长度为12米．另三边用总长为26米的木板材料围成．车棚形状如图1中的矩形 $A B C D$ ．为了方便学生出行，学校决定在与墙平行的一面开一个2米宽的门．

(1)、求这个车棚的最大面积是多少平方米？此时 $A B$ 与 $A D$ 的长分别为多少米？

(2)、如图2，在（1）的结论下，为了方便学生取车，施工单位决定在车棚内纵向、横向各修建2条、1条等宽的小路，使得停放自行车的面积为70平方米，那么小路的宽度是多少米

查看试题解析

五、解答题（三）（每小题12分，共24分）

22. 如图，点 $B$ 、 $C$ 、 $D$ 都在 $⊙ O$ 上，过点 $C$ 作 $A C ∥ B D$ 交 $O B$ 延长线于点 $A$ ，连接 $C D$ 、 $C O$ ，且 $∠ C D B = ∠ O B D = 30 °$ ， $B D = 6 \sqrt{3}$ cm．

(1)、求证： $A C$ 是 $⊙ O$ 的切线；

(2)、求 $⊙ O$ 的半径长；

(3)、求由弦 $C D$ 、 $B D$ 与弧 $B C$ 所围成的阴影部分的面积．

查看试题解析
23. 如图，已知抛物线 $y = - x^{2} + b x + c$ 与 $x$ 轴交于 $A (- 1 ， 0)$ ， $B (5 ， 0)$ 两点（点 $A$ 在点 $B$ 的左侧），与 $y$ 轴交于点 $C$ ．

(1)、求抛物线的解析式；

(2)、在抛物线的对称轴上存在一点 $P$ ，使得 $P A + P C$ 的值最小，求此时点 $P$ 的坐标；

(3)、点 $D$ 是第一象限内抛物线上的一个动点（不与点 $C$ 、 $B$ 重合），过点 $D$ 作 $D F ⊥ x$ 轴于点 $F$ ，交直线 $B C$ 于点 $E$ ，连接 $B D$ ，直线 $B C$ 把 $Δ B D F$ 的面积分成两部分，若 $S_{Δ B D E} ： S_{Δ B E F} = 3 ： 2$ ，请求出点 $D$ 的坐标．

查看试题解析