广东省河源市和平县2022-2023学年七年级下学期期末考试数学试卷
试卷更新日期:2023-07-28 类型:期末考试
一、选择题(本大题共10小题,每小题3分,共30分)
-
1. 下面各数中最小的数是( )A、 B、 C、 D、2. 球的体积是M,球的半径为R,则 , 其中变量和常量分别是( )A、变量是M,R;常量是π B、变量是R,π;常量是 C、变量是M,π;常量是3,4,π D、变量是M,R;常量是M3. 下列图形中是轴对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 4. 抛掷一枚质地均匀的正方体骰子,骰子各面分别标有数字1、2、3、4、5、6,则出现朝上的数字小于3的概率是( )A、 B、 C、 D、5. 已知一个角是40°,则这个角的余角的度数是( )A、30° B、40° C、50° D、60°6. 如图,直线 , 点是平行线外一点,连接 , , 若 , , 则的度数是( )
4. 抛掷一枚质地均匀的正方体骰子,骰子各面分别标有数字1、2、3、4、5、6,则出现朝上的数字小于3的概率是( )A、 B、 C、 D、5. 已知一个角是40°,则这个角的余角的度数是( )A、30° B、40° C、50° D、60°6. 如图,直线 , 点是平行线外一点,连接 , , 若 , , 则的度数是( ) A、22° B、24° C、26° D、28°7. 下列运算正确的是( )A、 B、 C、 D、8. 如图,已知 , 如果只添加一个条件(不加辅助线)使ΔABC≌ΔDEC,则添加的条件不能为( )
A、22° B、24° C、26° D、28°7. 下列运算正确的是( )A、 B、 C、 D、8. 如图,已知 , 如果只添加一个条件(不加辅助线)使ΔABC≌ΔDEC,则添加的条件不能为( ) A、 B、 C、 D、9. 若 , , 则等于( )A、25 B、1 C、21 D、2910. 如图,已知是的中线,E、F分别是和延长线上的点,且 , 连接 , 下列说法中:①;②;③;④ . 正确的是( )
A、 B、 C、 D、9. 若 , , 则等于( )A、25 B、1 C、21 D、2910. 如图,已知是的中线,E、F分别是和延长线上的点,且 , 连接 , 下列说法中:①;②;③;④ . 正确的是( )
 A、①②③ B、①②④ C、①③④ D、②③④
A、①②③ B、①②④ C、①③④ D、②③④二、填空题(本大题共5 小题,每小题 3 分,满分15分)
-
11. 若有一种病毒的直径大约为0.000000708 m,则0.000000708用科学记数法可表示为12. 某家庭电话月租费为10元,若市内通话费平均每次为0.2元,则该家庭一个月的话费y(元)与通话次数x(次)之间的关系式是 .13. 如图,△ABC中,AB的垂直平分线交AC于D,已知AC=10cm,BC=7cm,则△BCD的周长是cm.
 14. 如图,在 中, , 点为的中点,∠C=65° ,则∠BAD= .
14. 如图,在 中, , 点为的中点,∠C=65° ,则∠BAD= .
 15. 如图,已知 , 直线分别与直线、交于点Q,E,平分 , 交于G,若 , 则 .
15. 如图,已知 , 直线分别与直线、交于点Q,E,平分 , 交于G,若 , 则 .
三、解答题(一)(本大题共 3 小题,每小题 8分,共 24 分)
-
16. 计算:17. 先化简,再求值: , 其中 , .18. 如图,在中,
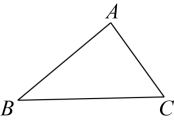 (1)、作的角平分线交于 , 作线段的垂直平分线分别交于 , 交于 , 垂足为(要求:尺规作图,保留作图痕迹,不写作法);(2)、在(1)的条件下,连接 , 则与边的位置关系是。
(1)、作的角平分线交于 , 作线段的垂直平分线分别交于 , 交于 , 垂足为(要求:尺规作图,保留作图痕迹,不写作法);(2)、在(1)的条件下,连接 , 则与边的位置关系是。四、解答题(二)(本大题共 3 小题,每小题 9分,共 27分)
-
19. 今年“6.18”互联网促销期间,某网红店开展有奖促销活动,凡进店购物的顾客均有转动8等分圆盘的机会,(如图),如果规定当圆盘停下来时指针指向1就中一等奖,指向3或8就中二等奖,指向2或4或6就中三等奖;指向其余数字不中奖.
 (1)、转动转盘,中一等奖、二等奖、三等奖的概率是分别是多少?(2)、顾客中奖的概率是多少?(3)、6月18日这天有1600人参与这项活动,估计这天获得一等奖的人数是多少?20. 父亲告诉小明“距离地面越高,温度越低”,并给小明出示了下面的表格.
(1)、转动转盘,中一等奖、二等奖、三等奖的概率是分别是多少?(2)、顾客中奖的概率是多少?(3)、6月18日这天有1600人参与这项活动,估计这天获得一等奖的人数是多少?20. 父亲告诉小明“距离地面越高,温度越低”,并给小明出示了下面的表格.距离地面的高度
0
1
2
3
4
5
温度/℃
20
14
8
2
根据上表,父亲还给小明出了下面几个问题,请你和小明一起回答.
(1)、上表反映了哪两个变量之间的关系?哪个是自变量?哪个是因变量?(2)、如果用表示距离地面的高度,用表示温度,那么随着的变化,是怎么变化的?请求出与之间的关系式.(3)、距离地面的高空的温度是多少?21. 如图,点、、、在同一条直线上,与相交于点 , , , . (1)、求证:;(2)、若 , , 求的度数.
(1)、求证:;(2)、若 , , 求的度数.五、解答题(三)(本大题共 2小题,每小题 12分,共24分)
-
22. “龟兔赛跑”的故事同学们都非常熟悉,图中的线段和折线表示“龟兔赛跑”时路程与时间的关系,请你根据图中给出的信息,解决下列问题.
 (1)、折线表示赛跑过程中的路程与时间关系,线段表示赛跑过程中的路程与时间的关系.(填“乌龟”和“兔子”)赛跑的全程是米.(2)、兔子在起初每分钟跑多少米?乌龟每分钟爬多少米?乌龟用了多少分钟追上了正在睡觉的兔子?(3)、兔子醒来,以800米/分的速度跑向终点,结果还是比乌龟晚到了0.5分钟,请你算一算兔子中间停下睡觉用了多少分钟?23. 如图
(1)、折线表示赛跑过程中的路程与时间关系,线段表示赛跑过程中的路程与时间的关系.(填“乌龟”和“兔子”)赛跑的全程是米.(2)、兔子在起初每分钟跑多少米?乌龟每分钟爬多少米?乌龟用了多少分钟追上了正在睡觉的兔子?(3)、兔子醒来,以800米/分的速度跑向终点,结果还是比乌龟晚到了0.5分钟,请你算一算兔子中间停下睡觉用了多少分钟?23. 如图 (1)、问题发现:两个顶角相等的等腰三角形,如果具有公共的顶角的顶点,并把它们的底角顶点连接起来,则形成一组全等的三角形,我们把具有这种规律的图形称为“手拉手”图形,
(1)、问题发现:两个顶角相等的等腰三角形,如果具有公共的顶角的顶点,并把它们的底角顶点连接起来,则形成一组全等的三角形,我们把具有这种规律的图形称为“手拉手”图形,如图1,和ΔADE是顶角相等的等腰三角形,即 , , 且 , 分别连接 , . 求证:;
(2)、类比探究:如图2,和ΔADE都是等腰三角形,即 , , 且 , B,C,D在同一条直线上.请判断线段与存在怎样的数量关系及位置关系,并说明理由.(3)、问题解决:如图3,若ΔACB和ΔDCE均为等腰直角三角形,且CA=CB,CD=CE,∠ACB=∠DCE=90°,点A,D,E在同一条直线上,CM为ΔDCE中DE边上的高,连接BE,若AE=7,BE=2,请直接写出CM的长,不说明理由.