浙江省绍兴市上虞区2022-2023学年八年级下学期期末数学试题

试卷更新日期：2023-07-28 类型：期末考试

进入出卷网下载

一、单选题

1. $\sqrt{2}$ × $\sqrt{3}$ =（）

A、 $\sqrt{5}$ B、 $\sqrt{6}$ C、2 $\sqrt{3}$ D、3 $\sqrt{2}$

查看试题解析
2. 已知关于x的一元二次方程 $x^{2} - 3 x + m = 0$ 的一个根为1，则m的值为（）

A、2 B、 $- 2$ C、4 D、-4

查看试题解析
3. 反比例函数 $y = - \frac{5}{3 x}$ 的比例系数为（）

A、 $- \frac{5}{3}$ B、-3 C、-5 D、 $- \frac{1}{3}$

查看试题解析
4. 某校对八年级各班进行卫生大评比，10个班的成绩汇总统计后制成如下表格：

平均数

众数

中位数

方差

9.3

9.2

9.4

0.2

学校规定该年级卫生评比要求：去掉一个最高分，去掉一个最低分后进行统计评比．则去掉最高和最低的两个分数后，表中相关的数据一定不发生变化的是（）

A、平均数 B、众数 C、中位数 D、方差

查看试题解析
5. 如图，在 $▱ A B C D$ 中，点 $E$ ， $F$ 分别在边 $B C$ ， $A D$ 上，连接 $A E$ ， $C F$ ， $A C$ ， $E F$ ，添加下列条件后不能使四边形 $A E C F$ 成为平行四边形的是（）

A、 $B E = D F$ B、 $A E ∥ C F$ C、 $O E = O F$ D、 $A F = A E$

查看试题解析

6. 下表记录了甲、乙、丙、丁四名学生参加班级女子立定跳远选拔赛成绩的平均数与方差

s^{2}

．根据表中数据，要从中选一名成绩好且发挥稳定的运动员参加比寒，最合适的人选是（）

	甲	乙	丙	丁
平均数（cm）	195	193	195	194
$s^{2} (c m^{2})$	5	5	12.5	15

A、甲 B、乙 C、丙 D、丁

查看试题解析

7. 在 $△ A B C$ 中，点D是边 $A C$ 的中点，连结 $B D$ 并延长到E，使 $D E = D B$ ，连结 $A E$ ， $C E$ ．则下列说法不正确的是（）

A、四边形 $A B C E$ 是平行四边形 B、当 $∠ A B C = 90 °$ 时，四边形 $A B C E$ 是矩形 C、当 $A B = B C$ 时，四边形 $A B C E$ 是菱形 D、当 $A B = B C = C A$ 时，四边形 $A B C E$ 是正方形

查看试题解析
8. 如图，在菱形 $A B C D$ 中， $∠ B = 60 °$ ，点 $O$ 为对称中心，点 $E$ 从点 $A$ 出发沿 $A B$ 向点 $B$ 移动，移动到点 $B$ 停止，连接 $E O$ 并延长交边 $C D$ 于点 $F$ ，连接 $E C$ ， $A F$ ．则四边形 $A E C F$ 形状的变化依次为（）

A、平行四边形→矩形→正方形→菱形 B、平行四边形→矩形→平行四边形→菱形 C、平行四边形→正方形→菱形→矩形 D、平行四边形→菱形→平行四边形→菱形

查看试题解析
9. 已知 $a (a > 1)$ 是关于x的方程 $x^{2} - b x + b - a = 0$ 的实数根．下列说法：①此方程有两个不相等的实数根；②当 $a = t ＋ 1$ 时，一定有 $b = t - 1$ ；③b是此方程的根；④此方程有两个相等的实数根．上述说法中，正确的有（）

A、①② B、②③ C、①③ D、③④

查看试题解析
10. 如图，一次函数 $y = - x + b$ 与反比例函数 $y = \frac{4}{x} (x > 0)$ 的图像相交于A、B两点，与x轴，y轴分别相交于C、D两点，连接OA、OB．过点A作 $A E ⊥ x$ 轴于点 $E$ ，交 $O B$ 于点 $F$ ．设点A的横坐标为 $m$ ．若 $S_{△ O A F} + S_{四边形 E F B C} = 4$ ，则 $m$ 的值为（）

A、1 B、 $\sqrt{2}$ C、2 D、4

查看试题解析

二、填空题

11. 二次根式 $\sqrt{x - 3}$ 中字母x的取值范围是．

查看试题解析
12. 如图，在矩形ABCD中，对角线AC，BD交于点O，已知∠AOD=120°，AB=2.5，则AC的长为．

查看试题解析
13. 某工厂第一车间有15名工人，每人日均加工螺杆数统计如图．则该车间工人日均生产螺杆数的中位数是个，众数是个．

查看试题解析
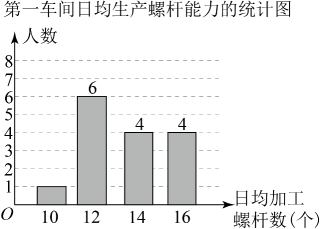14. 某网络学习平台2020年底的新注册用户数为100万，到2022年底的新注册用户数达到169万，设新注册用户数的年平均增长率为x，则可列出关于x的方程为．

查看试题解析
15. 如图， $E$ 是直线 $C D$ 上的一点，已知 $▱ A B C D$ 的面积为 $52 c m^{2}$ ，则 $Δ A B E$ 的面积为 $c m^{2}$ .

查看试题解析
16. 如图，由菱形通过添加一个合适的条件得到正方形．你所添加的一个条件是．

查看试题解析
17. 如图，在平面直角坐标系中，等腰 $R t △ A B C$ 的两直角边分别与坐标轴平行，直角顶点C的坐标为 $(1 ， 1)$ ， $A B = 3 \sqrt{2}$ ，若该三角形的顶点在反比例函数 $y = \frac{k}{x}$ 的图象上．则 $k =$ ．

查看试题解析
18. 如图，在 $△ A B C$ 中， $∠ A C B = 90 °$ ，点D为边 $A B$ 的中点，点E在边 $A C$ 上， $A E = B C = 2$ ，将 $△ B C E$ 沿BE折叠至 $△ B C^{'} E$ ，当 $C^{'} E ∥ C D$ 时，则 $B E =$ ．

查看试题解析

三、解答题

19. 解答下列各题：

(1)、计算： $\sqrt{{(- 10)}^{2}} - {(\sqrt{15})}^{2} + \sqrt{64}$ ．

(2)、已知点 $A (2 ， 1)$ ， $B (- 4 ， a)$ 在反比例函数 $y = \frac{k}{x} (k \neq 0)$ 的图象上，试求a的值．

查看试题解析
20. 解答下列各题：

(1)、用配方法解一元二次方程： $2 x^{2} + 4 x - 3 = 0$ ．

(2)、已知一组数据 $x_{1}$ ， $x_{2}$ ， $x_{3}$ ， $x_{4}$ 的平均数是5，求数据 $5 x_{1} - 5$ ， $5 x_{2} - 5$ ， $5 x_{3} - 5$ ， $5 x_{4} - 5$ 的平均数．

查看试题解析
21. 某校为了解初中学生每天的睡眠情况，随机调查了该校部分初中学生平均每天睡眠时间(单位：h)．根据调查结果，绘制出如下的统计图①和图②．

请根据相关信息，解答下列问题：

(1)、本次接受调查的学生人数为，图①中 $m$ 的值为．

(2)、求统计的这组学生平均每天睡眠时间数据的平均数、众数和中位数；

(3)、全校共有1000名学生，请估算全校学生平均每天睡眠时间不低于 $8 h$ 的人数．

查看试题解析
22. 如图，在 $▱ A B C D$ 中，点 $E$ ， $F$ 分别在边 $B C$ ， $A D$ 上，且 $B E = D F$ ，连结 $A E$ ， $C F$ ．

(1)、求证：四边形 $A E C F$ 是平行四边形．

(2)、连结 $A C$ ，若 $A C$ 平分 $∠ E A F$ ， $∠ A B C = 90 °$ ， $A B = 12$ ， $B C = 18$ ，求 $A F$ 的长．

查看试题解析

23. 温州某企业安排65名工人生产甲、乙两种产品，每人每天生产2件甲或1件乙，甲产品每件可获利15元.根据市场需求和生产经验，乙产品每天产量不少于5件，当每天生产5件时，每件可获利120元，每增加1件，当天平均每件利润减少2元.设每天安排x人生产乙产品.

(1)、根据信息填表：

产品种类	每天工人数(人)	每天产量(件)	每件产品可获利润(元)
甲			15
乙	x	x

(2)、若每天生产甲产品可获得的利润比生产乙产品可获得的利润多550元，求每件乙产品可获得的利润.

查看试题解析

24. 如图，已知正方形 $A B C D$ 的边长为2，点 $E$ 是边 $C D$ 上的一动点， $A F$ 平分 $∠ B A E$ 交边 $B C$ 于点 $F$ ．

(1)、①当点 $F$ 恰好是边 $B C$ 的中点时，求线段 $D E$ 长；②当点 $E$ 恰好是边CD的中点时，求线段 $B F$ 长．

(2)、猜想线段 $A E$ ， $D E$ ， $B F$ 之间的数量关系，并说明理由．

(3)、直接写 $△ A D E$ 与 $△ A B F$ 面积和的最大值．

查看试题解析

四、单选题

25. 如图，在边长为 $\sqrt{2}$ 的正八边形 $A B C D E F G H$ 中，已知I，J，K，L分别是边 $A H ， B C ， D E ， F G$ 上的动点，且满足 $I A = J C = K E = L G$ ，则四边形 $I J K L$ 面积的最大值为（）

A、 $4 + 2 \sqrt{2}$ B、 $2 + 2 \sqrt{2}$ C、 $4 + \sqrt{2}$ D、 $2 + 4 \sqrt{2}$

查看试题解析
26. 已知实数x，y满足 $(x^{2} + 4 x + 6) (9 y^{2} - 6 y + 5) = 8$ ，则 $y^{x}$ 的值为（）

A、－9 B、 $\frac{1}{9}$ C、9 D、 $- \frac{1}{9}$

查看试题解析

五、填空题

27. 如图，在菱形 $A B C D$ 中， $A B = 6$ ， $E$ 为 $C D$ 边上的三等分点， $∠ D = 60 °$ ，将 $△ A D E$ 沿 $A E$ 翻折得到 $△ A F E$ ，直线 $E F$ 交 $B C$ 于点 $P$ ，则 $P C =$ ．

查看试题解析
28. 若质数a，b满足 $a^{2} - 9 b - 4 = 0$ ，则数据a，b，2，3的中位数是．

查看试题解析

平均数	众数	中位数	方差
9.3	9.2	9.4	0.2