浙江省绍兴市柯桥区2022-2023学年八年级下学期期末数学试题
试卷更新日期:2023-07-28 类型:期末考试
一、单选题
-
1. 当时,二次根式的值为( )A、2 B、 C、 D、2. 下列图形中,既是轴对称图形又是中心对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 3. 如图,在中, , 则的度数是( )
3. 如图,在中, , 则的度数是( ) A、 B、 C、 D、4. 用配方法解方程 , 变形后的结果正确的是( )A、 B、 C、 D、5. 用反证法证明命题“在四边形中至少有一个内角不大于90°”时,首先应假设( )A、每个内角都小于90° B、每个内角都大于90° C、没有一个内角大于90° D、每个内角都等于90°6. 某射击队计划从甲、乙、丙、丁四名运动员中选拔一人参加国际射击比赛,在选拔过程中,每人射击10次,计算他们的平均成绩及方差如下表所示:
A、 B、 C、 D、4. 用配方法解方程 , 变形后的结果正确的是( )A、 B、 C、 D、5. 用反证法证明命题“在四边形中至少有一个内角不大于90°”时,首先应假设( )A、每个内角都小于90° B、每个内角都大于90° C、没有一个内角大于90° D、每个内角都等于90°6. 某射击队计划从甲、乙、丙、丁四名运动员中选拔一人参加国际射击比赛,在选拔过程中,每人射击10次,计算他们的平均成绩及方差如下表所示:甲
乙
丙
丁
/环
9.6
9.6
9.7
9.7
0.015
0.042
0.015
0.042

射击队决定依据他们的平均成绩及稳定性进行选拔,那么被选中的运动员是( )
A、甲 B、乙 C、丙 D、丁7. 某花圃用花盆培育某种花苗,经过试验发现,每盆花的盈利与每盆株数构成一定的关系,每盆植入3株时,平均单株盈利10元;以同样的栽培条件,若每盆每增加1株,平均单株盈利就减少1元,要使每盆的盈利为40元,需要每盆增加几株花苗?设每盆增加株花苗,下面列出的方程中符合题意的是( )A、 B、 C、 D、8. 已知点和点在反比例函数的图象上,若 , 则( )A、 B、 C、 D、9. 如图,已知正方形的面积为9.它的两个顶点 , 是反比例函数( , )的图象上两点,若点的坐标是 , 则的值为( )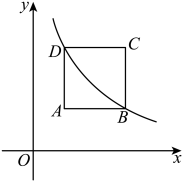 A、3 B、 C、 D、10. 如图所示,在一张长为 , 宽为的矩形纸片上,现要剪下一个腰长为的等腰三角形(要求:等腰三角形的一个顶点与矩形的一个顶点重合,其余的两个顶点在矩形的边上),则剪下的等腰三角形的面积不可能是( )
A、3 B、 C、 D、10. 如图所示,在一张长为 , 宽为的矩形纸片上,现要剪下一个腰长为的等腰三角形(要求:等腰三角形的一个顶点与矩形的一个顶点重合,其余的两个顶点在矩形的边上),则剪下的等腰三角形的面积不可能是( ) A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
11. 式子有意义,则x的取值范围是 .12. 为弘扬传统文化在端午节前夕,某校举行了“诗词竞赛”,某班15名同学参加了此次竞赛,他们的得分情况如下表所示,则全班15名同学的成绩的中位数是 .
人数
1
6
5
3
成绩(分)
70
80
90
100
13. 若一个多边形的内角和是其外角和的3倍,则这个多边形的边数是 .14. 关于的一元二次方程的一个根为-1,则的值为 .15. 如图,正方形的边长为1,连接 , 以点A为圆心,长为半径作弧,交直线于点 , 则的长是 . 16. 如图,过轴正半轴上一点作轴的平行线,分别与反比例函数和图象相交于点A和点 , 是轴上一点.若的面积为4,则的值为 .
16. 如图,过轴正半轴上一点作轴的平行线,分别与反比例函数和图象相交于点A和点 , 是轴上一点.若的面积为4,则的值为 .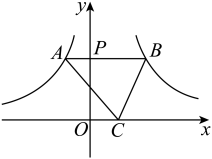 17. 母亲节,小敏准备送礼物给妈妈,他用正方形纸板,制作一个正方体礼品盒(如图所示裁剪).已知正方形纸板边长为10分米,则这个礼品盒的边长分米.
17. 母亲节,小敏准备送礼物给妈妈,他用正方形纸板,制作一个正方体礼品盒(如图所示裁剪).已知正方形纸板边长为10分米,则这个礼品盒的边长分米. 18. 如图1,在菱形中,对角线 , 相交于点 , 动点由点出发,沿运动,设点的运动路程为 , 的面积为 , 与的函数关系图象如图2,则的长为 .
18. 如图1,在菱形中,对角线 , 相交于点 , 动点由点出发,沿运动,设点的运动路程为 , 的面积为 , 与的函数关系图象如图2,则的长为 . 19. 如图,在平行四边形中, , , , 连结 , 将沿折叠得到 , 交于点 , 则的长度是 .
19. 如图,在平行四边形中, , , , 连结 , 将沿折叠得到 , 交于点 , 则的长度是 . 20. 如图,在平行四边形中, , , 是边延长线上一点,连接 , 以为边作等边三角形 , 连接 , 则的最小值是 .
20. 如图,在平行四边形中, , , 是边延长线上一点,连接 , 以为边作等边三角形 , 连接 , 则的最小值是 .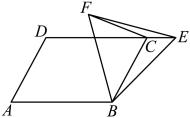
三、解答题
-
21. 计算:(1)、(2)、22. 用适当方法解方程:(1)、;(2)、 .23. 如图,中, , 是的角平分线,点为的中点,连接并延长至点 , 使 , 连接 , 和 . 证明四边形为平行四边形.
 24. 6月5日是世界环境日,某校组织了一次环保知识竞赛,每班选25名同学参加比赛,成绩分别为A、、、四个等级,其中相应等级的得分依次记为10分、9分、8分、7分,学校将某年级的八(1)班和八(2)班的成绩整理并绘制成统计图:根据提供的信息解答下列问题:
24. 6月5日是世界环境日,某校组织了一次环保知识竞赛,每班选25名同学参加比赛,成绩分别为A、、、四个等级,其中相应等级的得分依次记为10分、9分、8分、7分,学校将某年级的八(1)班和八(2)班的成绩整理并绘制成统计图:根据提供的信息解答下列问题:
班级
平均分
中位数
众数
方差
八(1)班
8.76
9
1.06
八(2)班
8.76
8
1.38
(1)、把八(1)班竞赛成绩统计图补充完整;(2)、写出表中 , 的值;(3)、依据数据分析表,有同学认为八(2)班的成绩比八(1)班好,但也有同学认为八(1)班的成绩更好,请你写出一条支持八(1)班成绩更好的理由.25. 如图所示,一次函数的图象与反比例函数交于 , 两点.(1)、求反比例函数的表达式;(2)、写出当一次函数大于反比例函数时,的取值范围.26. 根据以下素材,完成探索任务:如何故剪出符合要求的矩形纸片?
素材1
如图1,是腰长为的等腰直角三角形卡纸,甲,乙、丙三名同学分别用这样的卡纸试图裁剪出不一样的矩形纸片,并使长方形的四个顶点都在的边上.

素材2
甲同学按图2的方式裁剪,想裁出面积为的矩形纸片,乙同学按图3的方式裁剪,想裁出两边长之比为的矩形纸片,丙同学想裁出面积最大的矩形纸片.
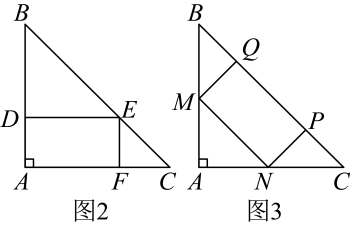
任务1
计算矩形纸片的边长
请帮甲同学计算此矩形纸片的两边长
任务2
计算矩形纸片的面积
请求出符合乙同学裁剪方案的矩形纸片的面积
任务3
计算矩形纸片的最大面积
请帮丙同学计算出面积最大的矩形纸片的面积
27. 在矩形中,是边上一动点,将矩形沿着对折,点的对应点为 .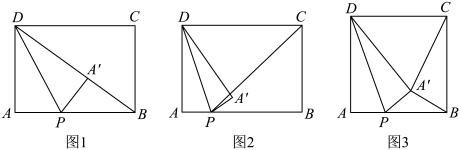 (1)、若 , .
(1)、若 , .①如图1,当点恰好落在对角线上时,求的长.
②如图2,是射线上一动点,当 , , 三点在同一直线上时,求的长.
(2)、如图3,若 , 连结 , , 当是直角时,求的长.