浙江省宁波市余姚市2022-2023学年八年级下学期期末数学试题
试卷更新日期:2023-07-28 类型:期末考试
一、单选题
-
1. 下列各式是最简二次根式的是( )A、 B、 C、 D、2. 数学世界奇妙无穷,其中曲线是微分几何的研究对象之一,下列数学曲线是中心对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 3. 方程经配方后,可化为( )A、 B、 C、 D、4. 在中, , 则( )A、 B、 C、 D、5. 为庆祝2023年5月30日神舟十六号成功发射,学校开展航天知识竞赛活动,经过几轮筛选,某班决定从甲、乙、丙、丁四名同学中选择一名同学代表班级参加比赛,经统计,四名同学成绩的平均数(单位:分)及方差(单位:分)如下表:
3. 方程经配方后,可化为( )A、 B、 C、 D、4. 在中, , 则( )A、 B、 C、 D、5. 为庆祝2023年5月30日神舟十六号成功发射,学校开展航天知识竞赛活动,经过几轮筛选,某班决定从甲、乙、丙、丁四名同学中选择一名同学代表班级参加比赛,经统计,四名同学成绩的平均数(单位:分)及方差(单位:分)如下表:甲
乙
丙
丁
平均数
97
95
97
93
方差
0.3
1.2
1.3
0.6
根据表中数据,要选一名成绩好且状态稳定的同学参赛,应选择( )
A、甲 B、乙 C、丙 D、丁6. 若一个正多边形的每个内角为 , 则这个多边形是( )A、六边形 B、八边形 C、十边形 D、十二边形7. 如图,在中, , , 的平分线交于点E,的平分线交于点F,则线段的长是( )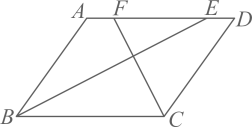 A、1 B、2 C、3 D、48. 已知点 , , 都在反比例函数的图象上,则下列关系式一定正确的是( )A、 B、 C、 D、9. 如图,矩形中,点为边的中点,连接 , 过作交于点 , 连接 , 若 , 则的度数为( )
A、1 B、2 C、3 D、48. 已知点 , , 都在反比例函数的图象上,则下列关系式一定正确的是( )A、 B、 C、 D、9. 如图,矩形中,点为边的中点,连接 , 过作交于点 , 连接 , 若 , 则的度数为( )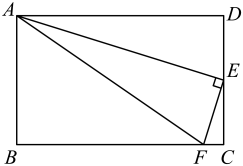 A、 B、 C、 D、10. 如图,一块边长为的正方形铁片,四角各被截去了一个边长为的小正方形,现在要从剩下的铁片中剪出一块完整的正方形铁片来,剪出的正方形面积最大为( )
A、 B、 C、 D、10. 如图,一块边长为的正方形铁片,四角各被截去了一个边长为的小正方形,现在要从剩下的铁片中剪出一块完整的正方形铁片来,剪出的正方形面积最大为( )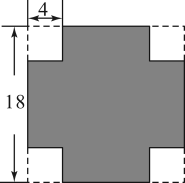 A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
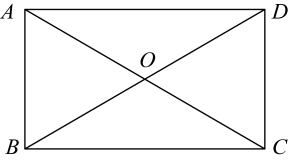
11. 若二次根式 有意义,则x的取值范围是 .12. 一元二次方程有两个相等的实数根,则k的值为.13. 如图,矩形的两条对角线交于点O,若 , 则 .
 14. 如图,要测量B,C两地的距离,小明想出一个方法:在池塘外取点A,得到线段AB、AC,并取AB、AC的中点D、E,连结DE.小明测得DE的长为a米,则B、C两地的距离为米.
14. 如图,要测量B,C两地的距离,小明想出一个方法:在池塘外取点A,得到线段AB、AC,并取AB、AC的中点D、E,连结DE.小明测得DE的长为a米,则B、C两地的距离为米. 15. 如图,在中, , 是的中线,若 , 则四边形的边上的高线长为 .
15. 如图,在中, , 是的中线,若 , 则四边形的边上的高线长为 .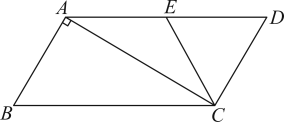 16. 如图,菱形的边在x轴的正半轴上,反比例函数的图象经过菱形对角线的中点D和顶点C,若菱形的面积为 , 则点C的坐标为 .
16. 如图,菱形的边在x轴的正半轴上,反比例函数的图象经过菱形对角线的中点D和顶点C,若菱形的面积为 , 则点C的坐标为 .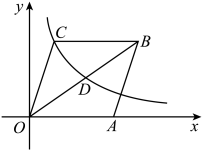
三、解答题
-
17. 计算:(1)、(2)、18. 解方程:(1)、(2)、19. 如图是由边长为1的小正方形构成的6×6的网格,点A,B均在格点上.
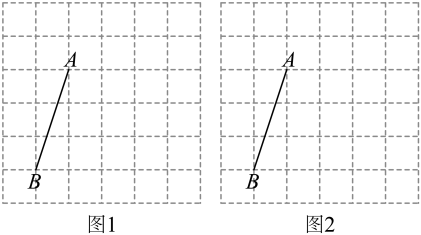 (1)、在图1的方格纸中画出以为一边的 , 点C,D均在格点上,且的面积为12(2)、在图2的方格纸中画出以为一边的菱形 , 点E,F均在格点上,且菱形的面积为820. 为了了解八年级学生的课外阅读情况,学校随机调查了该年级25名学生,得到他们上周双休日课外阅读时间(记为t,单位:时)的一组样本数据,其扇形统计图如图所示.
(1)、在图1的方格纸中画出以为一边的 , 点C,D均在格点上,且的面积为12(2)、在图2的方格纸中画出以为一边的菱形 , 点E,F均在格点上,且菱形的面积为820. 为了了解八年级学生的课外阅读情况,学校随机调查了该年级25名学生,得到他们上周双休日课外阅读时间(记为t,单位:时)的一组样本数据,其扇形统计图如图所示. (1)、阅读时间为4小时的占百分之几?(2)、试确定这个样本的中位数和众数,并求出平均数.21. 如图,一次函数与反比例函数的图象交于点 , .
(1)、阅读时间为4小时的占百分之几?(2)、试确定这个样本的中位数和众数,并求出平均数.21. 如图,一次函数与反比例函数的图象交于点 , .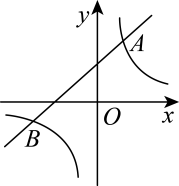 (1)、求反比例函数和一次函数的表达式.(2)、根据图象,当x取何值时,一次函数的值大于反比例函数的值?22. 随着科技的发展,某省正加快布局以5G等为代表的新兴产业.据统计,目前该省5G基站数量约为1.5万座,计划到今年底,全省5G基站数是目前的4倍;到后年底,全省5G基站数量将达到17.34万座.(1)、计划在今年底,全省5G基站数量是多少万座?(2)、按照计划,从今年底到后年底,全省5G基站数量的年平均增长率为多少?23. 定义:一个四边形的四条边和两条对角线这六条线段中只有两种长度,我们把这样的四边形叫做双距四边形.
(1)、求反比例函数和一次函数的表达式.(2)、根据图象,当x取何值时,一次函数的值大于反比例函数的值?22. 随着科技的发展,某省正加快布局以5G等为代表的新兴产业.据统计,目前该省5G基站数量约为1.5万座,计划到今年底,全省5G基站数是目前的4倍;到后年底,全省5G基站数量将达到17.34万座.(1)、计划在今年底,全省5G基站数量是多少万座?(2)、按照计划,从今年底到后年底,全省5G基站数量的年平均增长率为多少?23. 定义:一个四边形的四条边和两条对角线这六条线段中只有两种长度,我们把这样的四边形叫做双距四边形.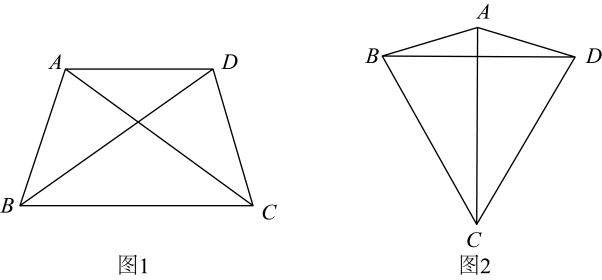 (1)、下列说法正确的有(填序号).
(1)、下列说法正确的有(填序号).①正方形一定是双距四边形.
②矩形一定是双距四边形.
③有一个内角为的菱形是双距四边形.
(2)、如图1,在四边形中, , , , 求证:四边形为双距四边形.(3)、如图2,四边形为双距四边形, , , , 求的长.24. 如图,已知矩形纸片 , , ().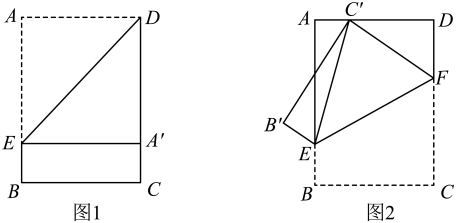 (1)、如图1,将矩形纸片沿过点D的直线折叠,使点A落在边上的点处,折痕交边于点E.求证:四边形是正方形.(2)、将图1中的矩形纸片沿过点E的直线折叠,使点C落在边上的点处,点B落在点处,折痕交边于点F,连结 , 如图2,
(1)、如图1,将矩形纸片沿过点D的直线折叠,使点A落在边上的点处,折痕交边于点E.求证:四边形是正方形.(2)、将图1中的矩形纸片沿过点E的直线折叠,使点C落在边上的点处,点B落在点处,折痕交边于点F,连结 , 如图2,①求证: .
②若 , , 求折痕的长.
③当为等腰三角形时,直接写出a,b之间应满足的数量关系.