浙江省舟山市2022-2023学年八年级下学期期末数学试题

试卷更新日期：2023-07-28 类型：期末考试

进入出卷网下载

一、单选题

1. 下列计算中，正确的是（）

A、 $\sqrt{{(- 3)}^{2}} = - 3$ B、 $\frac{\sqrt{9}}{\sqrt{6}} = \frac{\sqrt{6}}{2}$ C、 $\sqrt{3} \times \sqrt{6} = 6$ D、 $\sqrt{3^{2} + 4^{2}} = 7$

查看试题解析
2. 垃圾分类一小步，低碳生活一大步，垃圾桶上常有以下四种垃圾分类标识的图案，下列图案既是轴对称图形又是中心对称图形的是（）

A、 B、 C、 D、

查看试题解析
3. 用反证法证明“ $a < b$ ”时应假设（）

A、 $a > b$ B、 $a \geq b$ C、 $a = b$ D、 $a \leq b$

查看试题解析
4. 已知在▱ABCD中，若∠A+∠C=140°，则∠B的度数是（）

A、140° B、120° C、110° D、70°

查看试题解析
5. 一组数据：1、2、2、3，若添加一个数据2，则发生变化的统计量是（）

A、平均数 B、中位数 C、众数 D、方差

查看试题解析
6. 已知反比例函数 $y = \frac{a + 1}{x}$ 的图象位于第一、三象限，则a的取值范围是（）

A、 $a = - 1$ B、 $a \neq - 1$ C、 $a > - 1$ D、 $a < - 1$

查看试题解析
7. 如图，在菱形 $A B C D$ 中， $A C = 16 ， B D = 12 ，$ $E$ 是 $C D$ 边上一动点，过点 $E$ 分别作 $E F ⊥ O C$ 于点 $F ，$ $E F ⊥ O C$ 于点 $G ，$ 连接 $F G ，$ 则 $F G$ 的最小值为（）

A、 $4$ B、 $4.8$ C、 $5$ D、 $6$

查看试题解析
8. 在某渔民画展览中，有一幅长60cm，宽40cm的画，为给它的四周镶一条纸带，制成一幅矩形挂图（如图），如果要使整个挂图的面积是 $3500 c m^{2}$ ，设纸带的宽为x cm，那么x满足的方程是（）

A、 $(60 + x) (40 + 2 x) = 3500$ B、 $(60 + x) (40 + x) = 3500$ C、 $(60 + x) (40 + x) = 3500$ D、 $(60 + 2 x) (40 + 2 x) = 3500$

查看试题解析
9. 关于x的一元二次方程 $(a - 1) x^{2} + x + a^{2} - 1 = 0$ 的一个根是0，则a的值为（）

A、1 B、1或 $- 1$ C、 $- 1$ D、0.5

查看试题解析
10. 如图，在平面直角坐标系中， $△ O A B$ 的边 $O A$ 在x轴正半轴上，其中 $∠ O A B = 90 °$ ， $A O = A B$ ，点C为斜边 $O B$ 的中点，反比例函数 $y = \frac{k}{x} (k > 0 ， x > 0)$ 的图象过点C且交线段 $A B$ 于点D，连接 $C D$ ， $O D$ ，若 $S_{△ O C D} = \frac{3}{2}$ ，则 $\frac{S_{△ B C D}}{S_{△ O A D}}$ 的值为（）

A、 $\frac{5}{3}$ B、 $\frac{3}{2}$ C、 $\frac{5}{2}$ D、3

查看试题解析

二、填空题

11. 若代数式 $\sqrt{x - 2}$ 有意义，则x的取值范围是．

查看试题解析
12. 若一个正多边形的内角和是外角和的 $2$ 倍，则这个正多边形的边数为．

查看试题解析
13. 疫情期间居家学习，双胞胎姐妹小兰和小丽积极进行体育锻炼，增强体质．她们进行1分钟跳绳比赛，每人5次跳绳成绩的平均数都是105个，方差分别是s_小兰²＝1.6，s_小丽²＝2.2，则这5次跳绳成绩更稳定的是．（填“小兰”或“小丽”）

查看试题解析
14. 若关于x的方程 $2 x^{2} - m x + 3 = 0$ 有两个相等的实数根，则m的值是．

查看试题解析
15. 已知点 $(- 2 ， a)$ ， $(- 3 ， b)$ ， $(2 ， c)$ ，在函数 $y = - \frac{0.8}{x}$ 的图象上，则a，b，c三数的大小关系是（用“<”号连接）．

查看试题解析
16. 如图，在 $▱ A B C D$ 中，点E，F分别在 $A D$ 和 $A B$ 上，依次连接EB，EC，FC，FD，阴影部分面积分别为 $S_{1}$ ， $S_{2}$ ， $S_{3}$ ， $S_{4}$ ，已知 $S_{1} = 2$ ， $S_{2} = 17$ ， $S_{3} = 5$ ，则 $S_{4} =$ ．

查看试题解析

三、解答题

17. 化简或计算：

(1)、 $\sqrt{\frac{1}{2}} + \sqrt{18}$

(2)、 $(\sqrt{48} - \sqrt{27}) \div \sqrt{3}$

查看试题解析
18. 请用适当的方法解下列方程：

(1)、 $x^{2} - 2 x = 0$

(2)、 $x^{2} - 2 x - 6 = 0$

查看试题解析
19. 如图，在 $▱$ ABCD中，点E，F分别在BC，AD上，且BE=FD，求证：四边形AECF是平行四边形．

查看试题解析

20.

2023

年温州体育中考

1000

米改为选考项目，报名时小明在

1000

米与立定跳远之间犹豫.他把最近8次的成绩进行整理分析，具体操作如下：

【收集数据】小明最近8次的 $1000$ 米和立定跳远成绩.

次数

项目

$1000$ 米（分/秒）

$4 ： 00$

$3 ： 58$

$3 ： 55$

$3 ： 54$

$3 ： 56$

$3 ： 52$

$3 ： 50$

立定跳远（米）

$2.10$

$2.12$

$2.15$

$2.20$

$2.23$

$2.27$

$2.30$

$2.32$

【整理数据】依据中考标准分数表将1000米和立定跳远的成绩转化成相应分数，并绘制成折线统计图如图所示.

$1000$ 米和立定跳远的中考标准分数表（部分）

项目分值	$1000$ 米（分/秒）	立定跳远（米）
9分	$3 ： 35$	$2.38$
8分	$3 ： 45$	$2.30$
7分	$3 ： 55$	$2.22$
6分	$4 ： 05$	$2.14$
5分	$4 ： 15$	$2.06$

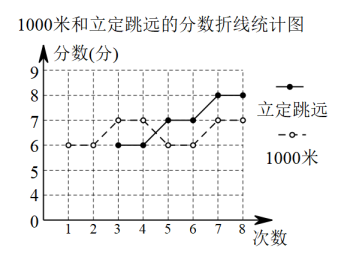
【应用数据】

(1)、根据以上数据，补全立定跳远折线统计图，并求出其平均分数.

(2)、已知

1000

米，立定跳远的方差分别为

0.25

（平方分），

1.25

平方分），根据所给的方差和（1）中所求的统计量，结合折线统计图，如果你是小明，会选择哪一项作为体育中考项目？请简述理由．

查看试题解析

21. 观察下列各式：
$\sqrt{1 + \frac{1}{1^{2}} + \frac{1}{2^{2}}} = 1 + \frac{1}{1} - \frac{1}{2} = \frac{3}{2}$ ； $\sqrt{1 + \frac{1}{2^{2}} + \frac{1}{3^{2}}} = 1 + \frac{1}{2} - \frac{1}{3} = \frac{7}{6}$ ； $\sqrt{1 + \frac{1}{3^{2}} + \frac{1}{4^{2}}} = 1 + \frac{1}{3} - \frac{1}{4} = \frac{13}{12}$

(1)、请你根据上面三个等式提供的信息，猜想： $\sqrt{1 + \frac{1}{4^{2}} + \frac{1}{5^{2}}} =$ ；

(2)、请你按照上面每个等式反映的规律，写出用n（n为正整）表示的等式，并验证；

(3)、利用上述规律计算 $\sqrt{\frac{50}{49} + \frac{1}{64}}$ ．

查看试题解析
22. 某租赁公司拥有80辆汽车．据统计，当每辆车的日租金为300元时，可全部租出．每辆车的日租金每增加5元，未租出的车将增加1辆．租出的车每辆每天的维护费为15元，未租出的车每辆每天的维护费为5 元．

(1)、当每辆车的日租金定为300元时，公司的当日日收益（租金收入扣除维护费）是多少元？

(2)、当每辆车的日租金定为360元时，能租出多少辆？

(3)、当每辆车的日租金定为多少元时，租赁公司的日收益（租金收入扣除维护费）可达23360元？

查看试题解析
23. 已知：一次函数 $y = a x + b$ 与反比例函数 $y = \frac{k}{x}$ 的图像在第一象限内交于点 $A (m ， 2)$ ， $B (3 ， n)$ 两点，且m，n满足 ${(2 m - 3 n)}^{2} + \sqrt{n - 1} = 0$ ，直线l经过点A且与y轴平行，点C是直线l上一点，过点C作 $C D ⊥ y$ 轴于点D，交反比例函数图象于点E．

(1)、求一次函数与反比例函数的函数表达式．

(2)、如图1，当点C在点A上方时，连接 $O C$ ， $O A$ ，且 $O C$ 平分 $∠ A O D$ ，求 $\frac{C D}{D E}$ 的值．

(3)、如图2，当点C在点A下方时，点H是 $D C$ 的中点，点G在x轴上，若四边形 $A B G H$ 是平行四边形．求出点 G的坐标．

查看试题解析
24. 问题情境：数学活动课上，同学们开展了以“矩形纸片折叠”为主题的探究活动（每个小组的矩形纸片规格相同），已知矩形纸片宽 $A D = 6$ ．

(1)、动手实践：如图1，A小组将矩形纸片 $A B C D$ 折叠，点D落在 $A B$ 边上的点E处，折痕为 $A F$ ，连接 $E F$ ，然后将纸片展平，得到四边形 $A E F D$ ．试判断四边形 $A E F D$ 的形状，并加以证明．

(2)、如图2，B小组将矩形纸片 $A B C D$ 对折使 $A B$ 与 $D C$ 重合，展平后得到折痕 $P Q$ ，再次过点A折叠使点D落在折痕 $P Q$ 上的点N处，得到折痕 $A M$ ，连结 $M N$ ，展平后得到四边形 $A N M D$ ，请求出四边形 $A N M D$ 的面积．

(3)、深度探究：
如图 3，C小组将图1中的四边形 $E F C B$ 剪去，然后在边 $A D ， E F$ 上取点G，H，将四边形 $A E F D$ 沿 $G H$ 折叠，使A点的对应点 $A^{'}$ 始终落在边 $D F$ 上（点 $A^{'}$ 不与点D，F重合），点E落在点 $E^{'}$ 处， $A^{'} E^{'}$ 与 $E F$ 交于点T．
探究①当 $A^{'}$ 在 $D F$ 上运动时， $△ F T A^{'}$ 的周长是否会变化？如变化，请说明理由；如不变，请求出该定值．

探究②直接写出四边形 $G A E H$ 面积的最小值．

查看试题解析