浙江省台州市椒江区2022-2023学年七年级下册数学期末试卷
试卷更新日期:2023-07-28 类型:期末考试
一、单选题
-
1. 在0、、-1、这四个数中,最小的数是( )A、0 B、 C、-1 D、
-
2. 点 在平面直角坐标系中所在的象限是( )A、第一象限 B、第二象限 C、第三象限 D、第四象限
-
3. 已知:如图,直线a,b被直线c所截,且a∥b,若∠1=70°,则∠2的度数是( )
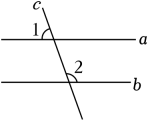 A、130° B、80° C、110° D、70°
A、130° B、80° C、110° D、70° -
4. 下列各组数中,是二元一次方程的一个解的是( )A、 B、 C、 D、
-
5. 在下列调查中,适宜采用全面调查的是( )A、了解某地所有中学生的体重情况 B、了解某校七(4)班学生校服的尺码情况 C、了解某地居民日平均用水量情况 D、调查某地学生上学所用的交通工具使用情况
-
6. 若 , a为任意实数,则下列结论正确的是( )A、 B、 C、 D、
-
7. 如图,将沿所在直线向右平移得到 , 已知 , , 则平移的距离为( )
 A、4 B、5 C、6 D、7
A、4 B、5 C、6 D、7 -
8. 已知方程组的解满足 , 则k的值为( )A、5 B、6 C、7 D、8
-
9. 小强在科学课上学过平面镜成像知识后,在老师的带领下到某厂房做验证实验,如图,老师在该厂房房檐处安装一平面镜 , 与墙面所成的角为 , 房顶与水平地面平行,小强在点M的正下方C处观察平面镜,恰能在M点看到水平地面上的点D.则的度数为( )
 A、 B、 C、 D、
A、 B、 C、 D、 -
10. 中国象棋中“马走日字”(“马”从两个小方格组成的“日”字的一角走到相对的另一对角,横着走竖着走都可以),如“马”从点出发,可到达A,B,C,D,E,F中任意一点,若“马”从点P出发连续走了n次“日”字后到达点 , 则n的最小值为( )
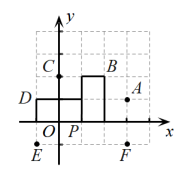 A、6 B、7 C、8 D、9
A、6 B、7 C、8 D、9
二、填空题
-
11. 36的算术平方根是
-
12. 已知是二元一次方程的解,则a的值是 .
-
13. 一组样本中,最大值为142,最小值为60,若取组距为10,则可以分为组.
-
14. 点在x轴上,则点A的坐标是 .
-
15. 在今年6.18网购狂欢节上,某网店商家对一电子产品进行打折促销,已知它的进价为800元,标价为1100元,商家为了保证利润率不低于 , 则至多可打折.
-
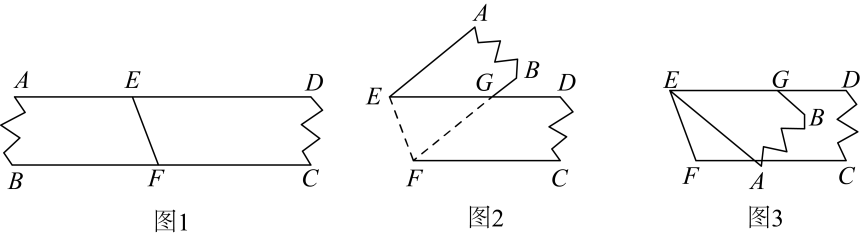
16. 如图1是等宽的纸条,点E、F分别在上,现将纸条沿折叠成图2形状,若此时 , 再沿折叠成图3,则图3中度数为 .
三、解答题
-
17. 计算:
-
18. 解不等式组: , 并在如图所示的数轴上表示不等式组的解集.

-
19. 如图,在正方形网格中,每个小正方形的边长均为1,格点三角形(顶点是网格线的交点的三角形)的顶点B,C的坐标分别是 .

⑴请在如图所示的网格内画出平面直角坐标系;
⑵把先向右平移4个单位,再向下平移3个单位得到 , 请在图中画出 , 并写出的坐标;
⑶在图中存在点D,使 , 直接写出D点坐标.
-
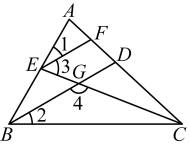
20. 如图,平分 , 点E在上,点F在上,与相交于点G. , 试说明 . (请通过填空完善下列推理过程)
解:∵(已知),
( ),
∴ ▲ ,
∴ ▲ ( ),
∴( ),
∵平分 ,
∴ ▲ ,
∴ .
-
21. 2023年第一季度我国经济稳步恢复,全国同比增速(“同比增速”指和上一年同期相比较的增长率)为 , 以下是以全国31省份2023年第一季度同比增速作为调查对象,绘制出的频数分布表和频数分布直方图,请结合图表完成下列问题:
组别
同比增速x(%)
频数
第1组
2
第2组
1
第3组
a
第4组
11
第5组
b
第6组
2
第7组
1
第8组
2
 (1)、填空: ▲ , ▲ , 并将频数分布直方图补充完整;(2)、以下对2023年一季度全国各省情况判断正确的是;(填写序号)
(1)、填空: ▲ , ▲ , 并将频数分布直方图补充完整;(2)、以下对2023年一季度全国各省情况判断正确的是;(填写序号)①大多数省份同比增速在;②所有省份同比增速不大于;③有半数以上省份同比增速超过;④已知北京同比增速为 , 则一季度北京处于全国中下水平;
(3)、请你根据题目所给信息写出两条不同于(2)中的结论. -
22. 如图,直线 , 垂足为点O,射线在内,满足 .
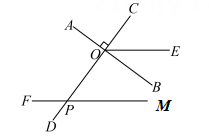 (1)、求的度数;(2)、在射线上取一点P,过点P作 , 求的度数.
(1)、求的度数;(2)、在射线上取一点P,过点P作 , 求的度数. -
23. 五一假期,小序一家自驾从椒江出发,沿途到A地和B地游玩,已知从椒江到A地的高速公路里程为150公里,非高速公路里程为20公里,共耗油14升;从A地到B地的高速公路里程为100公里,非高速公路里程为40公里,共耗油12升.(1)、分别求出小序家汽车在高速公路和非高速公路上平均每公里耗油各多少升;(2)、今年9月23日杭州举行亚运会开幕式,小序一家想去观看,经查询发现从椒江到杭州的动车票是127元一张(假设小序一家所有人都需要购买动车票),从椒江到杭州的高速公路里程为240公里,非高速公路里程为28公里,如果自驾从椒江到杭州的费用由油费和高速公路过路费两部分组成,已知高速公路过路费为120元,预估油费为8元每升,请问小序一家至少有几人去杭州时选择自驾的费用更省?
-
24. 对于平面直角坐标中的任意两点P,Q,若点P到两坐标轴的距离之和等于点Q到两坐标轴的距离之和,则称P,Q两点为“和合点”,如图1中的P,Q两点即为“和合点”.

 (1)、已知点 , , , .
(1)、已知点 , , , .①在上面四点中,与点为“和合点”的是 ▲ ;
②若点 , 过点F作直线轴,点G直线l上,A、G两点为“和合点”,则点G的坐标为 ▲ ;
③若点在第二象限,点在第四象限,且A、M两点为“和合点”,D、N两点为“和合点”,求a,b的值.
(2)、如图2,已知点 , , 点是线段上的一动点,且满足 , 过点作直线轴,若在直线m上存在点S,使得R,S两点为“和合点”,直接写出n的取值范围.
