2023-2024学年初中数学七年级上册9.12 完全平方公式同步分层训练培优卷(沪教版五四制)

试卷更新日期：2023-07-28 类型：同步测试

进入出卷网下载

一、选择题

1. 若 $(a^{2} + b^{2} + 1) (a^{2} + b^{2} - 1) = 35$ ，则 $a^{2} + b^{2} =$ （　　）

A、3 B、6 C、 $\pm 3$ D、 $\pm 6$

查看试题解析
2. 下列运算正确的是（　　）

A、 $a^{4} \cdot a^{3} = a^{7}$ B、 ${(a^{2})}^{3} = a^{5}$ C、 $3 a^{2} - a^{2} = 2$ D、 ${(a - b)}^{2} = a^{2} - b^{2}$

查看试题解析
3. 下列运算中，正确的是（）

A、 $a^{2} \cdot a^{5} = a^{10}$ B、 ${(a - b)}^{2} = a^{2} - b^{2}$ C、 $- 3 a^{2} b + 2 a^{2} b = - a^{2} b$ D、 ${(- 3 a^{3})}^{2} = 6 a^{6}$

查看试题解析
4. 如图，在长方形 $A B C D$ 中， $A B = 6 ， B C = 10$ ，其内部有边长为a的正方形 $A E F G$ 与边长为b的正方形 $H I J K$ ，两个正方形的重合部分也为正方形，且面积为5，若 $S_{2} = 5 S_{1}$ ，则正方形 $A E F G$ 与正方形 $H I J K$ 的面积之和为（）

A、29 B、25 C、 $\frac{49}{2}$ D、 $\frac{81}{4}$

查看试题解析
5. 现有一张边长为a的大正方形卡片和三张边长为b的小正方形卡片（ $\frac{1}{2} a < b < a$ ）如图1，取出两张小正方形卡片放入“大正方形卡片”内拼成的图案如图2，再重新用三张小正方形卡片放入“大正方形卡片”内拼成的图案如图3．已知图3中的阴影部分的面积比图2中的阴影部分的面积大 $2 a b - 6$ ，则小正方形卡片的面积是（）

A、2 B、3 C、4 D、5

查看试题解析
6. 有两个正方形A，B.现将B放在A的内部得图甲，将A，B构造新的正方形得图乙.若图甲和图乙中阴影部分的面积分别为1和12，若三个正方形A和两个正方形B得图丙，则阴影部分的面积为（　　）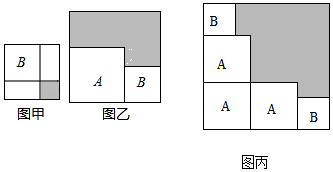

A、28 B、29 C、30 D、31

查看试题解析
7. 已知2ⁿ＋2¹²＋1（n＜0）是一个有理数的平方，则n的值为（）

A、﹣16 B、﹣14 C、﹣12 D、﹣10

查看试题解析
8. 如图，有A，B，C三种不同型号的卡片，每种各10张.A型卡片是边长为a的正方形，B型卡片是相邻两边长分别为a、b的长方形，C型卡片是边长为b的正方形.从中取出若干张卡片（每种卡片至少一张），把取出的这些卡片拼成一个正方形，所有符合要求的正方形的个数是（）

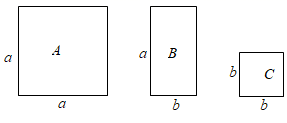A、4 B、5 C、6 D、7

查看试题解析

二、填空题

9. 已知 $a - b = 1$ ，则 $a^{3} - a^{2} b + b^{2} - 2 a b$ 的值为．

查看试题解析
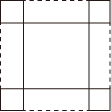
10. 配方法是数学中非常重要的一种思想方法，它是指将一个式子或将一个式子的某一部分通过恒等变形化为完全平方式或几个完全平方式的和的方法．这种方法常被用到代数式的变形中，并结合非负数的意义来解决问题．例如： $x^{2} - 4 x + 5$ 可配方成 ${(x - 2)}^{2} + 1$ ； $x^{2} + 2 x + 4$ 可配方成 ${(x + 1)}^{2} + 3$ ．若 $x^{2} + y^{2} - 2 x + 4 y + 5 = 0$ ，则 $x + y$ 的值为．

查看试题解析
11. $m > 0$ ， $n > 0$ ，若 $m^{2} + 4 n^{2} = 13$ ， $m n = 3$ ，请借助下图直观分析，通过计算求得 $m + 2 n$ 的值为．

查看试题解析
12. 已知（2021-a）（a-2022）＝5，则（a-2021）²+（a-2022）²＝．

查看试题解析

三、计算题

13. 已知 $m - n = 4$ ， $m n = - 3$ ．

(1)、计算： $m^{2} + n^{2}$ ；

(2)、求 $(m^{2} - 4) (n^{2} - 4)$ 的值；

(3)、求 $8^{m} \cdot 3 2^{n} \div 4^{m + 2 n}$ 的值．

查看试题解析

四、解答题

14. 先化简，再求值： [(x+2y)²-(x-2y)²-(x+2y)(x-2y)-4y²]÷2x，其中x=-2，y= $\frac{1}{2}$ ；

查看试题解析

五、综合题

15. 已知 $2 x + 3 y = 10$ ， $x y = 4$ ．

(1)、求 ${(2 x - 3 y)}^{2}$ 的值；

(2)、将长方形 $A B F C$ 和长方形 $C D E G$ 如图所示放置， $A B = 2 x$ ， $C D = 3 y$ ， $A C$ 、 $D E$ 的长分别为 $A B$ 、 $C D$ 的一半，求图中阴影部分的面积．

查看试题解析
16. 如图，将几个小正方形与小长方形拼成一个边长为 $(a + b + c)$ 的正方形．

(1)、若用不同的方法计算这个边长为 $(a + b + c)$ 的正方形面积，就可以得到一个等式，这个等式可以为．（只要写出一个即可）；

(2)、请利用（1）中的等式解答下列问题：
①若三个实数 $a ， b ， c$ 满足 $a + b + c = 11 ， a b + b c + a c = 38$ ，求 $a^{2} + b^{2} + c^{2}$ 的值；
②若三个实数 $x ， y ， z$ 满足 $2^{x} \times 4^{y} \div 8^{z} = \frac{1}{4} ， x^{2} + 4 y^{2} + 9 z^{2} = 44$ ，求 $2 x y - 3 x z - 6 y z$ 的值．

查看试题解析

2023-2024学年初中数学七年级上册9.12 完全平方公式 同步分层训练培优卷(沪教版五四制)

一、选择题

二、填空题

三、计算题

四、解答题

五、综合题

2023-2024学年初中数学七年级上册9.12 完全平方公式同步分层训练培优卷(沪教版五四制)