2023-2024学年初中数学七年级上册9.6 整式的加减 同步分层训练培优卷(沪教版五四制)
试卷更新日期:2023-07-28 类型:同步测试
一、选择题
-
1. 已知三角形的周长为 , 其中两边的和为 , 则此三角形第三边的长为( )A、 B、 C、 D、2. 现用同品质的A,B两种钢板制作某产品,有如下两种用料方案:方案1用5块A型钢板,9块B型钢板:方案2用4块A型钢板,10块B型钢板.已知每块A型钢板的面积比B型钢板大.设每块A型钢板和B型钢板的面积分别为x和y.从省料角度考虑,应选( )A、方案1 B、方案2 C、方案1与方案2都一样 D、无法确定3. , , 则M与N的大小关系为( )A、 B、 C、 D、无法确定4. 有自左向右依次排列的三个整式, , , , 将任意相邻的两个整式相加,所得之和等于在两个整式中间,可以产生一个整式串; , , , , , 这称为第1次“加法操作”;将第1次“加法操作”后的整式串按上述方法再做一次“加法操作”,可以得到第2次“加法操作”后的整式串;…,以此类推,下列说法:
①当时,第1次“加法操作”后,整式串中所有整式的积为负数;
②第次“加法操作”后,整式串中倒数第二个整式为;
③第4次“加法操作”后,整式串中所有整式之和为 .
其中正确的个数是( )
A、0 B、1 C、2 D、35. 有n个依次排列的整式:第一项是a2 , 第二项是a2+2a+1,用第二项减去第一项,所得之差记为b1 , 将b1加2记为b2 , 将第二项与b2相加作为第三项,将b2加2记为b3 , 将第三项与b3相加作为第四项,以此类推;某数学兴趣小组对此展开研究,得到4个结论:①b3=2a+5;
②当a=2时,第3项为16;
③若第4项与第5项之和为25,则a=7;
④第2022项为(a+2022)2;
⑤当n=k时,b1+b2+…+bk=2ak+k2;
以上结论正确的是( )
A、①②⑤ B、①③⑤ C、①②④ D、②④⑤6. 如图,将图1中的长方形纸片剪成①号、②号、③号、④号正方形和⑤号长方形,并将①号、②号、③号正方形按图2方式叠放入④号正方形内部,若需求出阴影部分的周长和,只需知道下列哪个正方形的边长( )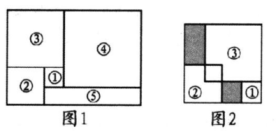 A、①号 B、②号 C、③号 D、④号7. 如图,用三个同图①的长方形和两个同图②的长方形用两种方式去覆盖一个大的长方形ABCD,两种方式未覆盖的部分(阴影部分)的周长相等,那么图①中长方形的面积S1与图②中长方形的面积S2的比是( )
A、①号 B、②号 C、③号 D、④号7. 如图,用三个同图①的长方形和两个同图②的长方形用两种方式去覆盖一个大的长方形ABCD,两种方式未覆盖的部分(阴影部分)的周长相等,那么图①中长方形的面积S1与图②中长方形的面积S2的比是( )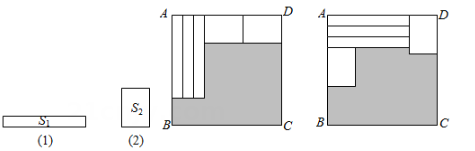 A、2:3 B、1:2 C、3:4 D、1:18. 对多项式x-y-z-m-n任意加括号后仍然只含减法运算并将所得式子化简,称之为“加算操作”,例如:(x-y)-(z-m-n)=x-y-z+m+n,x-y-(z-m)-n = x-y-z+m-n,……,
A、2:3 B、1:2 C、3:4 D、1:18. 对多项式x-y-z-m-n任意加括号后仍然只含减法运算并将所得式子化简,称之为“加算操作”,例如:(x-y)-(z-m-n)=x-y-z+m+n,x-y-(z-m)-n = x-y-z+m-n,……,给出下列说法:
①至少存在一种“加算操作”,使其结果与原多项式相等; ②不存在任何“加算操作”,使其结果与原多项式之和为0; ③所有的“加算操作”共有 8 种不同的结果.以上说法中正确的个数为( )
A、0 B、1 C、2 D、3二、填空题
-
9. 已知是方程的根,代数式的值是 .10. 如果一个两位数a的个位数字与十位数字都不是零,且互不相同,我们称这个两位数为“英华数”,定义新运算:将一个“英华数”的个位数字与十位数字对调,把这个新两位数与原两位数的和与11的商记 , 例如:a=13,对调个位数字与十位数字得到新两位数31,新两位数与原两位数的和,31+13=44,和与11的商44÷11=4,所以 . 根据以上定义,回答下列问题:(1)、计算: .(2)、若m,n都是“英华数”,且m+n=100,则 .11. 如图,用三个同(1)图的长方形和两个同(2)图的长方形用两种方式去覆盖一个大的长方形 , 两种方式未覆盖的部分(阴影部分)的周长一样,那么(1)图中长方形的面积与(2)图长方形的面积的比是.
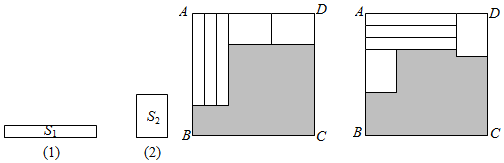 12. 已知 , 在关于 , 的二元一次方程组中, , , 则的取值范围是 , .
12. 已知 , 在关于 , 的二元一次方程组中, , , 则的取值范围是 , .三、计算题
-
13. 先化简,再求值: , 其中 .
四、解答题
-
14. 已知: , , 若 , 计算的值.15. 化简求值: , 其中x=3, .
五、作图题
-
16.(1)、(2)、(3)、画一条数轴,在数轴上标出以下各点,然后用“<”连接起来.
- ;-(-4);-|-1|; ;0; ;2.5;
六、综合题
-
