2023-2024学年初中数学七年级上册9.6 整式的加减同步分层训练基础卷(沪教版五四制)

试卷更新日期：2023-07-28 类型：同步测试

进入出卷网下载

一、选择题

1. 把两张形状大小完全相同的小长方形卡片（如图1）不重复地放在一个底面为长方形（长为8cm，宽为6cm）的盒子底部（如图2），盒子底面未被卡片覆盖的部分用阴影表示.则图2中两块阴影部分周长的和是（）

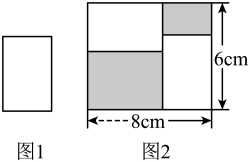A、28cm B、16cm C、32cm D、24cm

查看试题解析
2. 已知数a，b，c在数轴上的位置如图所示，化简|a+b|-|a-b|+|c-a|的结果为（）

A、-3a+c B、a-2b-c C、-a-2b+c D、-a+2b+c

查看试题解析
3. 如图，将三种大小不同的正方形纸片①，②，③和一张长方形纸片④，平铺长方形桌面，重叠部分（图中阴影部分）是正方形，若要求长方形桌面长与宽的差，只需知道（）

A、正方形①的边长 B、正方形②的边长 C、阴影部分的边长 D、长方形④的周长

查看试题解析
4. 图1是由3个相同小长方形拼成的图形其周长为24 $c m$ ，图2中的长方形 $A B C D$ 内放置10个相同的小长方形，则长方形 $A B C D$ 的周长为（）

A、 $32 c m$ B、 $36 c m$ C、 $48 c m$ D、 $60 c m$

查看试题解析
5. 有一道题目是一个多项式A减去多项式2x²+5x-3，小胡同学将2x²+5x-3抄成了2x²+5x+3，计算结果是-x²+3x-7，这道题目的正确结果是（）

A、x²+8x-4 B、-x²+3x-1 C、-3x²-x-7 D、x²+3x-7

查看试题解析
6. 若A＝x²-xy，B＝xy+y² ，则3A-2B为（）

A、3x²-2y²-5xy B、3x²-2y² C、-5xy D、3x²+2y²

查看试题解析
7. 如图，将图1中的长方形纸片剪成①号、②号、③号、④号正方形和⑤号长方形，并将①号、②号、③号正方形按图2方式叠放入④号正方形内部，若需求出阴影部分的周长和，只需知道下列哪个正方形的边长（）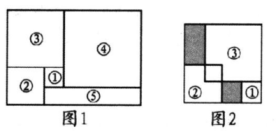

A、①号 B、②号 C、③号 D、④号

查看试题解析
8. 如图，用三个同图①的长方形和两个同图②的长方形用两种方式去覆盖一个大的长方形ABCD，两种方式未覆盖的部分(阴影部分)的周长相等，那么图①中长方形的面积S₁与图②中长方形的面积S₂的比是（）

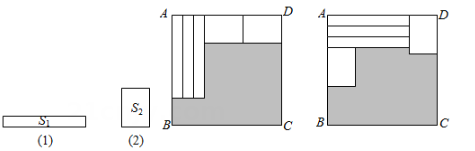A、2：3 B、1：2 C、3：4 D、1：1

查看试题解析

二、填空题

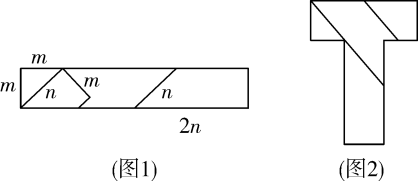
9. 如果一个多项式减去 $2 y^{2} + 3 x^{2}$ 的差等于 $2 x^{2} - y^{2}$ ，那么这个多项式是

查看试题解析
10. 已知 $M = m - 4$ ， $N = m^{2} - 3 m$ ，则M与N的大小关系为MN（填>、<或=）

查看试题解析
11. 2022年11月3 日，中国空间站“T”字基本构型在轨组装完成，“T”寓意：睿智，卓越．图1是用长方形纸板做成的四巧板(已知线段长度如图所示)，用它拼成图2的“T”字型图形，则“T”字型图形的周长为． (用含m，n的式子表示)

查看试题解析
12. 如图，将边长为4的正方形和半径为2的圆叠放在一起，两个空白部分的面积分别为 $m ， n (m > n)$ ，则 $m - n$ 的值为（结果保留 $π$ ）.

查看试题解析
13. 一个多项式加上 $3 x^{2} - 6 x + 4$ 得到 $- 7 x^{2} + x + 1$ ，则这个多项式是.

查看试题解析
14. 一个多项式与 $- x^{2} - 2 x + 10$ 的和是 $3 x - 2$ ，则这个多项式为.

查看试题解析

三、计算题

15. 先化简，再求值：6xy²-4x²y-3（xy²- $\frac{2}{3}$ x²y），其中x＝2，y＝-1.

查看试题解析

四、解答题

16. 先化简，再求值： $4 x y - 2 x y - (- 3 x y)$ ，其中 $x = 2$ ， $y = - 1$ .

查看试题解析
17. 先化简，再求值： $8 x^{2} y - 2 (3 x^{2} y - x y) - x y$ ，其中， $x = - 3 ， y = 2$ .

查看试题解析
18. 先化简，再求值： $(x^{2} y - 2 x y^{2}) - 3 (2 x y^{2} - x^{2} y)$ ，其中 $x = \frac{1}{2}$ ， $y = - 1$ .

查看试题解析

五、作图题

19.

(1)、 $x - (3 x + 1) - 2 (4 - x)$

(2)、 $+ (5 a - 3 b) - (a - 2 b)$

(3)、画一条数轴，在数轴上标出以下各点，然后用“＜”连接起来.
- $\frac{5}{2}$ ；-（-4）；-|-1|； $（ -1 ）^{2}$ ；0； ${-2}^{2}$ ；2.5；

查看试题解析

六、综合题

20. 先化简，再求值：4xy－2xy－（－3xy），其中x＝2，y＝－1.

查看试题解析
21. 已知关于 $x$ 的多项式 $A$ ， $B$ ，其中 $A = m x^{2} + 2 x - 1$ ， $B = x^{2} - n x + 2$ （ $m$ ， $n$ 为有理数）.

(1)、化简 $2 B - A$ ；

(2)、若 $2 B - A$ 的结果不含 $x$ 项和 $x^{2}$ 项，求 $m$ 、 $n$ 的值.

查看试题解析
22. 某公司生产一种电子产品和配件，已知该电子产品的售价为200元/台，配件的售价为20元/个，在促销活动期间，有如下两种优惠方案（顾客只能选择其中一种优惠方案）：
①买一台电子产品送一个配件；
②电子产品每台降价10元出售，配件每个打9折.
在促销活动期间，某学校计划到该公司购买 $x$ 台电子产品， $y$ 个配件 $(y > x > 0)$ .

(1)、分别求该校选择优惠方案①，②购买该电子产品和配件所需的总费用；（用含x、y的代数式来表示）

(2)、若该校计划购买该电子产品10台，配件20个，请通过计算判断，选择哪种优惠方案更省钱？

查看试题解析

2023-2024学年初中数学七年级上册9.6 整式的加减 同步分层训练基础卷(沪教版五四制)

一、选择题

二、填空题

三、计算题

四、解答题

五、作图题

六、综合题

2023-2024学年初中数学七年级上册9.6 整式的加减同步分层训练基础卷(沪教版五四制)