2023-2024学年初中数学七年级上册9.2 代数式同步分层训练培优卷(沪教版五四制)

试卷更新日期：2023-07-28 类型：同步测试

进入出卷网下载

一、选择题

1. 宝安公园是深圳西部最美丽的市政公园之一，公园植被种类丰富，空气清新，风景秀丽，最高山峰海拔125米.小亮和同学利用周末去爬宝安公园，已知他们上山的速度为 $v_{1}$ 米/秒，下山的速度为 $v_{2}$ 米/秒，若他们上山和下山所走的路程相同，则他们爬山的平均速度为（）米/秒.

A、 $\frac{v_{1} + v_{2}}{2}$ B、 $\frac{v_{1} + v_{2}}{v_{1} v_{2}}$ C、 $\frac{v_{1} v_{2}}{v_{1} + v_{2}}$ D、 $\frac{2 v_{1} v_{2}}{v_{1} + v_{2}}$

查看试题解析
2. 某企业今年1月份产值为 $a$ 万元，2月份比1月份减少了10%，3月份比2月份增加了15%，则3月份的产值是（）

A、 $(a - 10 %) (a + 15 %)$ 万元 B、 $a (1 - 90 %) (1 + 85 %)$ 万元 C、 $a (1 - 10 %) (1 + 15 %)$ 万元 D、 $a (1 - 10 % + 15 %)$ 万元

查看试题解析
3. 随着国产芯片自主研发的突破，某种型号芯片的价格经过两次降价，由原来每片a元下降到每片b元，已知第一次下降了 $10 ％$ ，第二次下降了20%，则a与b满足的数量关系是（）

A、 $b = a (1 - 10 ％ - 20 ％)$ B、 $b = a (1 - 10 ％) (1 - 20 ％)$ C、 $a = b (1 + 10 ％ + 20 ％)$ D、 $a = b (1 + 10 ％) (1 + 20 ％)$

查看试题解析
4. 如图，正方形 $A B C D$ 与正方形 $B E F G$ ，点 $C$ 在边 $B G$ 上，已知正方形 $A B C D$ 的边长 $a$ ，正方形 $B E F G$ 的边长为 $b (a < b)$ ，用 $a$ 、 $b$ 表示下列面积， $D E$ 与 $G B$ 相交于点 $H$ ，下列各选项中错误的是（）

A、 $S_{△ D A E} = S_{梯形 A B G D}$ B、 $S_{△ D H G} = S_{△ H B E}$ C、 $S_{△ D E G} = S_{正方形 A B C D}$ D、 $S_{△ D E G} = S_{△ G B E}$

查看试题解析
5. 如图，大矩形分割成五个小矩形，④号、⑤号均为正方形，其中⑤号正方形边长为1．若②号矩形的长与宽的差为2，则知道哪个小矩形的周长，就一定能算出这个大矩形的面积（）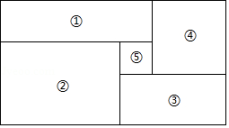

A、①或③ B、② C、④ D、以上选项都可以

查看试题解析
6. 如图所示的大长方形被分割成4个大小不同的正方形(1)(2)(4)和一个小长方形(5)，有下列结论：
（ 1 ）若已知小正方形(1)和(2)的周长，就能求出大长方形的周长；（2）若已知小正方形(3)的周长，就能求出大长方形的周长；（3）若已知小正方形(4)的周长，就能求出大长方形的周长；(4) 若已知小长方形(5)的周长，就能求出大长方形的周长。其中正确的是（）

A、(1) (2) (4) B、(1) (2) (3) C、(1) (3) D、(2) (3)

查看试题解析
7. 买一个足球需 $m$ 元，买一个篮球需 $n$ 元，则买5个足球和4个篮球共需（）

A、 $9 m n$ 元 B、 $20 m n$ 元 C、 $(4 m + 5 n)$ 元 D、 $(5 m + 4 n)$ 元

查看试题解析
8. 张师傅下岗再就业，做超了小商品生意，某次进货时，他以每件a元的价格购进了20件甲种小商品，每件b元的价格购进了30件乙种小商品（ $a > b$ ）回来后，根据市场行情，他将这两种小商品都以每件 $\frac{a + b}{2}$ 元的价格出售，在这次买卖中，张师傅是（）

A、赔钱 B、赚钱 C、不赚不赔 D、无法确定赚和赔

查看试题解析

二、填空题

9. 2023长春马拉松于5月21日在南岭体育场鸣枪开跑，某同学参加了7.5公里健康跑项目，他从起点开始以平均每分钟x公里的速度跑了10分钟，此时他离健康跑终点的路程为公里．（用含x的代数式表示）

查看试题解析
10. 某校计划给每个年级配发n套劳动工具，则3个年级共需配发套劳动工具．

查看试题解析
11. 如图，长方形 $A B C D$ 中放入一个边长为 $8$ 的大正方形 $A L M N$ 和两个边长为6的小正方形 $D E F G$ 及正方形 $H I J K$ ．

(1)、若阴影部分 $S_{2}$ 与 $S_{3}$ 为正方形，且 $S_{2}$ 的面积为1，则 $S_{3} =$ ．

(2)、若3个阴影部分的面积满足 $2 S_{3} + S_{1} - S_{2} = 12$ ，则长方形 $A B C D$ 的面积为．

查看试题解析
12. 如图是一组有规律的图案，它们是由边长相等的等边三角形组合而成，照此规律摆下去，摆成第50个图案需要个等边三角形．

查看试题解析
13. 用适当的符号表示：m的2倍与n的差是非负数：．

查看试题解析

三、解答题

14. 小明坐计程车，发现：
请用x表示y.

查看试题解析
15. 利民商店出售一种商品原价为a，有如下几种方案：
（1）先提价10％，再降价10％；（2）先降价10％，再提价10％；（3）先提价20％，再降价20％。问用这三种方案调价的结果是否一样？最后是不是都恢复了原价？

查看试题解析

四、综合题

16. “端午节”是中华民族古老的传统节日．甲、乙两家超市在“端午节”当天对一种原来售价相同的粽子分别推出了不同的优惠方案．
甲超市方案：购买该种粽子超过200元后，超出200元的部分按95% 收费；
乙超市方案：购买该种粽子超过300元后，超出300元的部分按90% 收费．
设某位顾客购买了x元的该种粽子．

(1)、补充表格，填写在“横线”上：
x（单位：元）
实际在甲超市的花费（单位：元）
实际在乙超市的花费（单位：元）
0＜x≤200
x
x
200＜x≤300

x
x ＞300



(2)、当x为何值时？到甲、乙两超市的花费一样．

(3)、如果顾客在“端午节”当天购买该种粽子超过300元，那么到哪家超市花费更少？说明理由．

查看试题解析
17. 如图

(1)、【操作感知】如图①，长方形透明纸上有一条数轴， $A B$ 是周长为4的圆的直径，点 $A$ 与数轴原点重合，将圆从原点出发沿数轴正方向滚动1周，点 $A$ 落在数轴上的点 $A^{'}$ 处；将圆从原点出发沿数轴负方向滚动半周，点 $B$ 落在数轴上的点 $B^{'}$ 处，折叠长方形透明纸，使数轴上的点 $A^{'}$ 与点 $B^{'}$ 重合，此时折痕与数轴交点表示的数为.

(2)、【建立模型】折叠长方形透明纸，使得数轴上表示数 $a$ 的点 $M$ 与表示数 $b$ 的点 $N$ 重合，则折痕与数轴交点表示的数为（用含 $a$ ， $b$ 的代数式表示）.

(3)、【问题解决】若 $C$ ， $D$ ， $E$ 为数轴上不同的三点，点 $C$ 表示的数为 $4$ ，点 $D$ 表示的数为-2，如果 $C$ ， $D$ ， $E$ 三点中的一点到其余两点的距离相等，求点 $E$ 表示的数；

(4)、如图②，若 $A B$ 是周长为 $3$ 的圆的直径，点 $A$ 与数轴原点重合，将圆从原点出发沿数轴正方向滚动2周，点 $A$ 落在数轴上的点 $Q$ 处；将圆从原点出发沿数轴负方向滚动 $1$ 周，点 $A$ 落在数轴上的点 $P$ 处.将此长方形透明纸沿 $P$ ， $Q$ 剪开，将点 $P$ ， $Q$ 之间一段透明纸对折，使其左、右两端重合，这样连续对折 $n$ 次后，再将其展开，求最右端折痕与数轴交点表示的数.

查看试题解析

x（单位：元）	实际在甲超市的花费（单位：元）	实际在乙超市的花费（单位：元）
0＜x≤200	x	x
200＜x≤300		x
x ＞300

2023-2024学年初中数学七年级上册9.2 代数式 同步分层训练培优卷(沪教版五四制)

一、选择题

二、填空题

三、解答题

四、综合题

2023-2024学年初中数学七年级上册9.2 代数式同步分层训练培优卷(沪教版五四制)