北京市房山区2022-2023学年七年级下学期数学期末考试试卷
试卷更新日期:2023-07-28 类型:期末考试
一、单选题
-
1. 一元一次不等式的解集在数轴上表示如图所示,该不等式的解集为( )
 A、 B、 C、 D、2. 纳米(nm)技术是一种高新科技,它可以在微观世界里直接探索范围内物质的特性,从而创造新材料. , 将数字0.000000001用科学记数法表示应为( )A、 B、 C、 D、3. 下列式子从左到右变形是因式分解的是( )A、 B、 C、 D、4. 下列计算正确的是( )A、 B、 C、 D、5. 如图,直线 , 相交于点O, , 若 , 则的度数为( )
A、 B、 C、 D、2. 纳米(nm)技术是一种高新科技,它可以在微观世界里直接探索范围内物质的特性,从而创造新材料. , 将数字0.000000001用科学记数法表示应为( )A、 B、 C、 D、3. 下列式子从左到右变形是因式分解的是( )A、 B、 C、 D、4. 下列计算正确的是( )A、 B、 C、 D、5. 如图,直线 , 相交于点O, , 若 , 则的度数为( ) A、36° B、54° C、64° D、144°6. 下列命题中,假命题是( )A、同角的补角相等 B、同一平面内,过一点有且只有一条直线与已知直线垂直 C、如果 , , 那么 D、两条直线被第三条直线所截,同旁内角互补7. 下列图形中,由AB∥CD,能得到∠1=∠2的是( )A、
A、36° B、54° C、64° D、144°6. 下列命题中,假命题是( )A、同角的补角相等 B、同一平面内,过一点有且只有一条直线与已知直线垂直 C、如果 , , 那么 D、两条直线被第三条直线所截,同旁内角互补7. 下列图形中,由AB∥CD,能得到∠1=∠2的是( )A、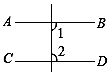 B、
B、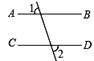 C、
C、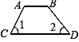 D、
D、 8. 如果 是方程 的解, 是正整数,则 的最小值是( )A、3 B、4 C、5 D、6
8. 如果 是方程 的解, 是正整数,则 的最小值是( )A、3 B、4 C、5 D、6二、填空题
-
9. 已知 , 则的补角是°.10. 计算: .11. 如图,利用工具测量角,则的大小为 .
 12. 写出一个以为解的二元一次方程组: .13. 如图,已知 , 请你添加一个条件: , 使得 .
12. 写出一个以为解的二元一次方程组: .13. 如图,已知 , 请你添加一个条件: , 使得 .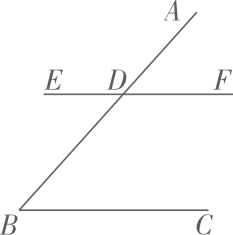 14. 用一组 的值说明命题“若 ,则 ”是假命题,这组值可以是 . (按 的顺序填写)15. 某学习小组对学校附近一超市年月至月西红柿价格进行调研,结果统计如下表:(价格:元/千克)
14. 用一组 的值说明命题“若 ,则 ”是假命题,这组值可以是 . (按 的顺序填写)15. 某学习小组对学校附近一超市年月至月西红柿价格进行调研,结果统计如下表:(价格:元/千克)月份
月
月
月
月
月
月
月
月
价格
上表中西红柿价格的平均数为 .
16. 已知二元一次方程 , 当时,的取值范围是 .三、解答题
-
17. 计算:(1)、;(2)、 .18. 解方程组: .19. 解不等式组:20. 把下列各式分解因式:(1)、;(2)、21. 如图, , 点在边上.
 (1)、过点作直线 , 交于点;(2)、过点作直线 , 过点作直线 , 直线 , 交于点 .(3)、如果 , 那么22. 已知 , 求代数式的值.23. 完成下面的证明.
(1)、过点作直线 , 交于点;(2)、过点作直线 , 过点作直线 , 直线 , 交于点 .(3)、如果 , 那么22. 已知 , 求代数式的值.23. 完成下面的证明.如图,AB和CD相交于点O,∠C=∠COA,∠D=∠BOD.

求证:AC∥BD.
证明:∵∠C=∠COA,∠D=∠BOD,
又∠COA=∠BOD( )
∴∠C= ▲
∴AC∥BD( )
24. 某中学积极开展“阳光体育”运动,开设“足球课间活动”.购买了甲种品牌的足球个,乙种品牌的足球个,共花费元,已知乙种品牌足球的单价比甲种品牌足球的单价高30元.(1)、求甲、乙两种品牌足球的单价各多少元?(2)、为参加“足球联谊赛”活动,根据需要,学校决定再次购进甲、乙两种品牌的足球50个.正逢体育用品商店“优惠促销”活动,甲种品牌的足球单价优惠4元,乙种品牌的足球单价打8折.如果此次学校购买甲、乙两种品牌足球的总费用不超过元,且购买乙种品牌的足球不少于个,那么有几种购买方案?25. 下面是解答一道几何题时添加辅助线的方法,请完成证明.已知:如图, .
求证: .
证明:如图,过点作直线 .
 26. 北京时间2023年6月4日,神舟十五号载人飞船返回舱在东风着陆场成功着陆,神舟十五号载人飞行任务取得圆满成功.为了激发学生的航天兴趣,弘扬科学棈神,某校七年级所有学生参加了“科技筑梦 创新成长”为主题的太空科普知识竞赛.为了解七年级学生的科普知识掌握情况,调查小组进行了抽样调查,过程如下,请补充完整.(1)、收集数据:调查小组计划从七年级选取20名学生的竞赛成绩(百分制)作为样本,下面的抽样方法中,合理的是____(填字母).A、从七年级的科技小组中选取20名学生的竞赛成绩组成样本; B、从七年级选取20名男生的竞赛成绩组成样本; C、从七年级随机选取10名男生、10名女生的竞赛成绩组成样本.(2)、抽样方法确定后,调查小组抽取得到的样本数据如下:
26. 北京时间2023年6月4日,神舟十五号载人飞船返回舱在东风着陆场成功着陆,神舟十五号载人飞行任务取得圆满成功.为了激发学生的航天兴趣,弘扬科学棈神,某校七年级所有学生参加了“科技筑梦 创新成长”为主题的太空科普知识竞赛.为了解七年级学生的科普知识掌握情况,调查小组进行了抽样调查,过程如下,请补充完整.(1)、收集数据:调查小组计划从七年级选取20名学生的竞赛成绩(百分制)作为样本,下面的抽样方法中,合理的是____(填字母).A、从七年级的科技小组中选取20名学生的竞赛成绩组成样本; B、从七年级选取20名男生的竞赛成绩组成样本; C、从七年级随机选取10名男生、10名女生的竞赛成绩组成样本.(2)、抽样方法确定后,调查小组抽取得到的样本数据如下:66 88 84 79 92 83 95 89 100 91
91 97 74 77 99 98 89 94 100 100
整理、描述数据:按如下分数段整理、描述的样本数据情况如下:
成绩
人数
2
3
7
(3)、分析数据样本数据的平均数、中位数、众数如下表所示:平均数
中位数
众数
89.3
得出结论:
a. ,
b.如果该校七年级共有200名同学,估计成绩不低于95分的有人.
27. 线段 , 交于点 , 为直线上一点(不与点 , 重合).过点在的右侧作射线 , 过点作直线 , 交于点(与不重合).(1)、如图1,若点在线段上,且为钝角.①按要求补全图形;
②判断与的数量关系,并证明.
 (2)、若点在线段的延长线上,请直接写出与的数量关系
(2)、若点在线段的延长线上,请直接写出与的数量关系