北京市丰台区2022-2023学年七年级下学期数学期末考试试卷
试卷更新日期:2023-07-28 类型:期末考试
一、单选题
-
1. 在下列各组由运动项目的图标组成的图形中,能将其中一个图形只经过平移得到另一个图形的是( )A、
 B、
B、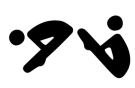 C、
C、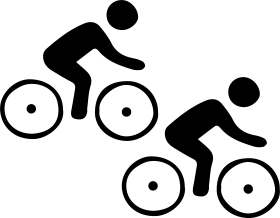 D、
D、 2. 9的平方根是( )A、3 B、±3 C、 D、±3. 以下调查中,适宜抽样调查的是( )A、了解某班学生喜爱的体育运动项目的情况 B、合唱节前,某班计划购买服装,统计同学们的服装尺寸大小 C、了解某地区饮用水矿物质含量的情况 D、旅客上飞机前的安全检查4. 不等式的解集在数轴上表示正确的是( )A、
2. 9的平方根是( )A、3 B、±3 C、 D、±3. 以下调查中,适宜抽样调查的是( )A、了解某班学生喜爱的体育运动项目的情况 B、合唱节前,某班计划购买服装,统计同学们的服装尺寸大小 C、了解某地区饮用水矿物质含量的情况 D、旅客上飞机前的安全检查4. 不等式的解集在数轴上表示正确的是( )A、 B、
B、 C、
C、 D、
D、 5. 如图所示,将一块三角板的直角顶点放在直尺的一边上,若 , 则的大小是( )
5. 如图所示,将一块三角板的直角顶点放在直尺的一边上,若 , 则的大小是( ) A、 B、 C、 D、6. 如果是关于和的二元一次方程的解,那么的值是( )A、 B、1 C、2 D、37. 有如下四个命题:
A、 B、 C、 D、6. 如果是关于和的二元一次方程的解,那么的值是( )A、 B、1 C、2 D、37. 有如下四个命题:①无理数是无限不循环小数;
②连接直线外一点与直线上各点的所有线段中,垂线段最短;
③如果 , 那么:
④两条直线被第三条直线所截,同旁内角互补
其中,所有正确命题的序号是( )
A、①②③ B、①② C、③④ D、②④8. 如图,在平面直角坐标系中,点的坐标为 . 线段以每秒旋转90°的速度,绕点沿顺时针方向连续旋转,同时,点从点出发,以每秒移动1个单位长度的速度,在线段上,按照…的路线循环运动,则第2023秒时点的坐标为( )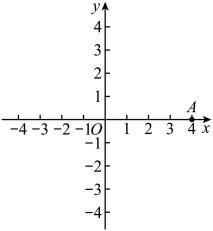 A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
9. 写出一个绝对值大于2且小于3的无理数 .10. 如果 , 那么.11. 用不等式表示“a的3倍与b的和是非负数”,应为 .12. 如图,只需添加一个条件,即可以证明 , 这个条件可以是 . (写出一个即可)
 13. 下面是2018年-2022年中国新能源汽车保有量的统计图,2022年新能源汽车保有量比2021年增加了万辆,从2019年到2022年新能源汽车保有量年增长率最大的是年.
13. 下面是2018年-2022年中国新能源汽车保有量的统计图,2022年新能源汽车保有量比2021年增加了万辆,从2019年到2022年新能源汽车保有量年增长率最大的是年. 14. , 是平面直角坐标系中的两点,连接 , 当线段长度最小时,b的值为 , 线段长为 .15. 如图在4×4的正方形网格中,每个小正方形的边长均为1,点 , , 均在格点(小正方形的顶点)上.在网格中建立平面直角坐标系,且 , . 如果点是点平移后的对应点,点按点的平移过程进行平移,且平移后的对应点为 , 那么点的坐标是 .
14. , 是平面直角坐标系中的两点,连接 , 当线段长度最小时,b的值为 , 线段长为 .15. 如图在4×4的正方形网格中,每个小正方形的边长均为1,点 , , 均在格点(小正方形的顶点)上.在网格中建立平面直角坐标系,且 , . 如果点是点平移后的对应点,点按点的平移过程进行平移,且平移后的对应点为 , 那么点的坐标是 . 16. 小明沿着某公园的环形跑道(周长大于)按逆时针方向跑步,并用跑步软件记录运动轨迹,他从起点出发,每跑 , 软件会在运动轨迹上标注出相应的里程数.前的记录数据如图所示,当小明跑了2圈时,他的运动里程数(填“”“=”或“”);如果小明跑到时恰好回到起点,那么此时小明总共跑的圈数为 .
16. 小明沿着某公园的环形跑道(周长大于)按逆时针方向跑步,并用跑步软件记录运动轨迹,他从起点出发,每跑 , 软件会在运动轨迹上标注出相应的里程数.前的记录数据如图所示,当小明跑了2圈时,他的运动里程数(填“”“=”或“”);如果小明跑到时恰好回到起点,那么此时小明总共跑的圈数为 .
三、解答题
-
17. 计算: .18. 解方程组: .19. 解不等式组: .20. 如图,P为的边上一点.
 (1)、根据下列语句按要求画图.
(1)、根据下列语句按要求画图.①过点P画的垂线a;
②过点P画的平行线b;
(2)、在(1)的条件下,若 , 则直线a与直线b形成的四个角的度数分别是 .21. 已知:如图, , 于点 , .求证: .

完成如下证明.
证明:∵ ,
∴( )(填推理的依据).
∵ ,
∴ .
∴( )(填推理的依据).
∴ .
∵ ,
∴ .
∴ .
∴ .
22. 青春期是青少年生长发育的关键时期,这一时期的青少年需要通过合理的膳食以满足生长发育的需求,某学校想了解本校-岁的学生能量摄入情况,从本校-岁的学生中抽取名学生,对名学生某天能量摄入值(单位:千卡)进行了调查、收集与整理,下面给出了部分信息. 能量摄入值(单位:千卡)频数分布表:
组别
能量摄入值
频数
第1组
第2组
第3组
第4组
第5组
b.能量摄入值(单位:千卡)的频数分布直方图及扇形图:

请根据以上信息,完成下列问题:
(1)、写出 , , 的值;(2)、补全频数分布直方图;(3)、根据《中国学龄儿童膳食指南()》,-岁的学龄儿童的能量需要水平是千卡天,如果该校-岁的学生共有人,请你估计该校-岁的学生当日能量摄入值(单位:千卡)在的人数.23. 如图,在平面直角坐标系中,直线l经过原点O和点 . (1)、①在图中描出点 , , , ;
(1)、①在图中描出点 , , , ;②在点 , , , 中,位于直线l左上方的点是;位于直线l右下方的点是;
(2)、若点位于直线l的左上方,则b的取值范围是 .24. 北京丰台站是亚洲最大铁路枢纽客站.北京丰台站交通枢纽是北京丰台站的重要配套工程,设计施工中采用了绿色建筑设计及建造技术,通过设置空气源热泵、节能灯具、高性能建材等,节约能源及建筑材料.北京丰台站交通枢纽将在2023年年内实现主体结构封顶.施工单位租用两种车型为交通枢纽运送高性能建材,若用2辆A型车和1辆B型车载满高性能建材,一次可运送10吨:用1辆A型车和2辆B型车载满高性能建材,一次可运送11吨.根据以上信息,解答下列问题:
(1)、1辆A型车和1辆B型车都载满高性能建材,一次分别可运送多少吨?(2)、现有高性能建材31吨,计划同时租用A型车a辆,B型车b辆,一次运完且恰好每辆车都载满高性能建材.①请你帮施工单位列出所有可能的租车方案:
②若1辆A型车需租金300元/次,1辆B型车需租金320元/次,则最少的租车费是元
25. 如图1,线段 , 为线段上一动点(不与点 , 重合).分别连接 , . 过点在线段的右侧作射线 , 使 , 作的角平分线 . (1)、如图2,当与重合时,求证:;(2)、当与不重合时,直接用等式表示 , , 之间的数量关系.26. 对于平面直角坐标系xOy中的点和图形G,给出如下定义:将图形G向右或向左平移个单位长度,再向上或向下平移个单位长度,得到图形 , 称图形为图形G关于点M的“伴随图形”.
(1)、如图2,当与重合时,求证:;(2)、当与不重合时,直接用等式表示 , , 之间的数量关系.26. 对于平面直角坐标系xOy中的点和图形G,给出如下定义:将图形G向右或向左平移个单位长度,再向上或向下平移个单位长度,得到图形 , 称图形为图形G关于点M的“伴随图形”. (1)、如图1.点 .
(1)、如图1.点 .①若点 , 点为点E关于点M的“伴随图形”,则点的坐标为;
②若点 , 点为点T关于点M的“伴随图形”,且点在第一象限,求t的取值范围;
(2)、如图2, , , , , 图形H是正方形关于点M的“伴随图形”.当图形H只在第一或第四象限,且与正方形有公共点时,直接写出的取值范围.