北京市朝阳区2022-2023学年七年级下学期数学期末考试试卷

试卷更新日期：2023-07-28 类型：期末考试

进入出卷网下载

一、单选题

1. 如图，过点P作线段 $A B$ 的垂线，垂足在（）

A、线段 $A B$ 上 B、线段 $A B$ 的延长线上 C、线段 $A B$ 的反向延长线上 D、直线 $A B$ 外

查看试题解析
2. 在平面直角坐标系中，点P（2，﹣3）在（　　）

A、第一象限 B、第二象限 C、第三象限 D、第四象限

查看试题解析
3. 下列说法正确的是（）

A、无限小数都是无理数 B、无理数都是无限小数 C、带根号的数都是无理数 D、所有有理数都可以用数轴上的点表示，反过来，数轴上的所有点都表示有理数

查看试题解析
4. 把方程 $2 x - y = 3$ 改写成用含x的式子表示y的形式，正确的是（）

A、y=2x-3 B、y=3-2x C、 $2 x = y + 3$ D、 $x = \frac{y + 3}{2}$

查看试题解析
5. 如图，直线 $A B ， C D$ 相交于点O， $O A$ 平分 $∠ E O C$ ，若 $∠ E O C = 80 °$ ，则 $∠ B O D$ 的度数为（）

A、 $30 °$ B、 $40 °$ C、 $80 °$ D、 $100 °$

查看试题解析
6. 某个不等式的解集在数轴上的表示如图所示，下列判断正确的是（）

A、这个不等式有最大整数解，是－2 B、这个不等式有最大整数解，是－1 C、这个不等式有最小整数解，是－2 D、这个不等式有最小整数解，是－1

查看试题解析
7. 《国家节水行动方案》由国家发改委、水利部于2019年4月15日印发并实施，方案中提出，到2022年，全国用水总量控制在6700亿立方米以内．小明根据国家就计局公布的2010－2022年全国用水总量（单位：亿立方米）的有关数据给制了如下统计图，并添加了一条靠近尽可能多散点的直线来表示用水量的发展趋势．
根据统计图信息，下列推断不合理的是（）

A、《国家节水行动方案》确定的2022年节点目标已完成 B、2010－2022年全国用水总量呈下降趋势 C、根据2010－2022年全国用水总量的发展趋势，估计2023年全国用水总量约为5700亿立方米 D、根据2020－2022年全国用水总量的发展趋势，估计2023年全国用水总量约为6100亿立方米

查看试题解析
8. 如图，把一个周长为定值的长方形（长小于宽的3倍）分割为五个四边形，其中A是正方形，周长记为 $l_{1}$ ， B和D是完全一样的长方形，周长记为 $l_{2}$ ， C和E是完全一样的正方形，周长记为 $l_{3}$ ，下列为定值的是（）

A、 $l_{1} ， l_{2}$ B、 $l_{1} ， l_{3}$ C、 $l_{2} ， l_{3}$ D、 $l_{1} ， l_{2} ， l_{3}$

查看试题解析

二、填空题

9. 我国于2020年开展了第七次全国人口普查，这是一次调查（填“全面”或“抽样”）．

查看试题解析
10. $\sqrt{9}$ 的平方根是

查看试题解析
11. 写出二元一次方程 $x - y + 3 = 0$ 的一个解：．

查看试题解析
12. a与5的和不小于2，用不等式表示为：．

查看试题解析
13. 比较两数的大小： $2 \sqrt{2}$ 3．

查看试题解析
14. 在平面直角坐标系 $x O y$ 中，A，B两点的坐标如图所示，三角形 $O A B$ 的面积为．

查看试题解析
15. 可以用一个m的值说明命题“正数一定大于它的算术平方根”是假命题，这个值可以是 $m =$ ．

查看试题解析
16. 在平面直角坐标系xOy中，将一个横、纵坐标都是整数的点，沿平行（或垂直）于坐标轴的直线平移1个单位长度，称为该点走了1步．点 $A (1 ， 0)$ ， $B (2 ， 4)$ ， $C (3 ， 1)$ 各走了若干步后到达同一点P，当点P的坐标为时，三个点的步数和最小，为．

查看试题解析

三、解答题

17. 计算： $\sqrt[3]{- 27} - \sqrt{3} (1 - \sqrt{3}) + | \sqrt{2} - \sqrt{3} |$ ．

查看试题解析
18. 解方程组： ${\begin{array}{l} x + \frac{y}{2} = 2 ， \\ 3 x - 2 y = - 1 . \end{array}$

查看试题解析
19. 解不等式 $5 x + 3 \geq 3 x - 1$ ，并在数轴上表示解集．

查看试题解析
20. ${\begin{array}{l} 2 x + 3 \geq x + 11 \\ \frac{2 x + 5}{3} - 1 < 2 - x \end{array}$

查看试题解析
21. 完成下面的证明．
已知：如图，直线a，b，c被直线l所截， $∠ 1 + ∠ 2 = 180 °$ ， $∠ 1 = ∠ 3$ ．求证： $b ∥ c$ ．

证明：∵ $∠ 1 + ∠ 2 = 180 °$ ，
∴ $a ∥$        ▲       （  ）．
∵ $∠ 1 = ∠ 3$ ，
∴ $a ∥$        ▲  （  ）．
∴ $b ∥ c$ （  ）．

查看试题解析
22. 列方程组解应用题：
活动课上小明想用天平称量甲、乙两类型小球的质量，但只有一个10克的砝码，反复试验后，他发现以下两种情况，天平左右平衡．

天平左边
天平右边
天平状态
记录一
5个甲类型小球，1个10克砝码
10个乙类型小球
平衡
记录二
15个甲类型小球
20个乙类型小球，1个10克砝码
平衡
已知每个同类型小球的质量都相同，请求出1个甲类型小球和1个乙类型小球的质量分别是多少克．

查看试题解析
23. 在同一平面内有5条互不重合的直线，共有6个不同的交点，画出它们可能的位置关系．（画出三种不同的示意图，并指出其中互相平行的直线）

查看试题解析
24. 为了参加全校各年级之间的广播操比赛，七年级准备从63名同学中挑选身高差不多的40名同学参加比赛．为此收集到这63名同学的身高（单位：cm），并绘制了频数分布表和频数分布直方图．
身高分组
频数
          $149 \leq x < 153$
2
          $153 \leq x < 157$
a
          $157 \leq x < 161$
23
          $161 \leq x < 165$
13
          $165 \leq x < 169$
9
          $169 \leq x < 173$
3

根据以上信息，解答下列问题：

(1)、请根据题中已有信息写出a的值，并补全频数分布直方图；

(2)、此绘制选择的组距为；

(3)、体育委员认为依据此频数分布直方图不能很好地解决这个问题，请你分析他的理由，并写出如何调整可能会更好．

查看试题解析
25. 在三角形 $A B C$ 中， $∠ C = 60 °$ ，将线段 $A B$ 沿直线 $B C$ 平移得到线段 $D E$ （点D与点B对应，且不与点B，C重合），连接 $A E$ ， $∠ A E D$ 和 $∠ A C D$ 的平分线所在直线相交于点P（点P不与点C，E重合）．

(1)、如图1， $∠ B = 40 °$ ，
①依题意补全图1；
②求 $∠ E P C$ 的度数；

(2)、若 $∠ B = α$ ，直接写出 $∠ E P C$ 的度数．（用含α的式子表示）

查看试题解析
26. 在平面直角坐标系 $x O y$ 中，对于不共线的三个点给出如下定义：若这三个点都落在同一个正方形的边上，且这个正方形的边分别与两条坐标轴平行（或垂直），则这个正方形边长的最小值称为这三个点的外方距．已知点 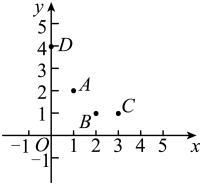$A (1 ， 2) ， B (2 ， 1) ， C (3 ， 1) ， D (0 ， 4)$ ．

(1)、点A，B，C的外方距为；

(2)、以下三个点中存在外方距的是；（只填序号）
①A，B，D ②A，C，D ③B，C，D

(3)、 $P (m ， n)$ ，若点A，B，P的外方距为3，直接写出m，n需要满足的条件．

查看试题解析

	天平左边	天平右边	天平状态
记录一	5个甲类型小球，1个10克砝码	10个乙类型小球	平衡
记录二	15个甲类型小球	20个乙类型小球，1个10克砝码	平衡

身高分组	频数
$149 \leq x < 153$	2
$153 \leq x < 157$	a
$157 \leq x < 161$	23
$161 \leq x < 165$	13
$165 \leq x < 169$	9
$169 \leq x < 173$	3