北京市东城区2022-2023学年七年级下学期数学期末考试试卷
试卷更新日期:2023-07-28 类型:期末考试
一、单选题
-
1. 如图,小手盖住的点的坐标可能为( )
 A、 B、 C、 D、2. 4 的算术平方根是( )A、2 B、±2 C、16 D、±163. 下列调查方式,最适合全面调查的是( )A、检测某品牌鲜奶是否符合食品卫生标准 B、了解某班学生一分钟跳绳成绩 C、了解北京市中学生视力情况 D、调查某批次汽车的抗撞击能力4. 若是关于 , 的二元一次方程的解,则的值为( )A、2 B、3 C、5 D、75. 实数 , 对应的位置如图所示,下列式子正确的是( )
A、 B、 C、 D、2. 4 的算术平方根是( )A、2 B、±2 C、16 D、±163. 下列调查方式,最适合全面调查的是( )A、检测某品牌鲜奶是否符合食品卫生标准 B、了解某班学生一分钟跳绳成绩 C、了解北京市中学生视力情况 D、调查某批次汽车的抗撞击能力4. 若是关于 , 的二元一次方程的解,则的值为( )A、2 B、3 C、5 D、75. 实数 , 对应的位置如图所示,下列式子正确的是( ) A、 B、 C、 D、6. 如图,直线 , 相交于点 , , 垂足为点 . 若 , 则的度数为( )
A、 B、 C、 D、6. 如图,直线 , 相交于点 , , 垂足为点 . 若 , 则的度数为( ) A、 B、 C、 D、7. 如图,在数轴上,与表示的点最接近的点是( )
A、 B、 C、 D、7. 如图,在数轴上,与表示的点最接近的点是( ) A、点 B、点 C、点 D、点8. 已知二元一次方程组则的值为( )A、 B、 C、1 D、39. 如图为小丽和小欧依次进入电梯时,电梯因超重而警示音响起的过程,且过程中没有其他人进出.
A、点 B、点 C、点 D、点8. 已知二元一次方程组则的值为( )A、 B、 C、1 D、39. 如图为小丽和小欧依次进入电梯时,电梯因超重而警示音响起的过程,且过程中没有其他人进出.
已知当电梯乘载的重量超过400千克时警示音响起,且小丽、小欧的重量分别为50千克、70千克.若小丽进入电梯前,电梯内已乘载的重量为千克,则的取值范围是( )
A、 B、 C、 D、10. 2023年国家统计局公布了《2022年国民经济和社会发展统计公报》.公报显示了全国2018年至2022年货物进出口额的变化情况,根据国家统计局2022年发布的相关信息,绘制了如下的统计图.根据统计图提供的信息,下列结论正确的是( )
①与2018年相比,2019年的进口额的年增长率虽然下降,但进口额仍然上升;
②从2018年到2022年,进口额最多的是2022年;
③2018—2022年进口额年增长率持续下降;
④与2021年相比,2022年出口额增加了2.3万亿元
A、①②④ B、①②③ C、①③④ D、①②③④二、填空题
-
11. “m的2倍与5的和是正数”可以用不等式表示为 .12. 如图,斑马线的作用是为了引导行人安全地通过马路.小丽觉得行人沿垂直马路的方向过斑马线更为合理,这一想法体现的数学依据是 .
 13. 北京中轴线南起永定门,北至钟鼓楼,全长7.8千米.如图是利用平面直角坐标系画出的中轴线及其沿线部分地点分布图,若这个坐标系分别以正东、正北方向为轴、轴的正方向,表示天安门的点的坐标为 , 表示王府井的点的坐标为 , 则表示永定门的点的坐标为 .
13. 北京中轴线南起永定门,北至钟鼓楼,全长7.8千米.如图是利用平面直角坐标系画出的中轴线及其沿线部分地点分布图,若这个坐标系分别以正东、正北方向为轴、轴的正方向,表示天安门的点的坐标为 , 表示王府井的点的坐标为 , 则表示永定门的点的坐标为 . 14. 如图,直径为1个单位长度的圆从原点沿数轴向右滚动一周(不滑动),圆上的一点由原点到达点O′,点O′所对应的数值是 .
14. 如图,直径为1个单位长度的圆从原点沿数轴向右滚动一周(不滑动),圆上的一点由原点到达点O′,点O′所对应的数值是 . 15. 如图,将含有的直角三角板的两个顶点分别放在直尺的一组对边上,如果 , 那么°.
15. 如图,将含有的直角三角板的两个顶点分别放在直尺的一组对边上,如果 , 那么°. 16. 如图,一块边长为10米的正方形花园,在上面修了一条道路,路的宽都是1米,其余部分种上各种花草,则种植花草的面积是平方米.
16. 如图,一块边长为10米的正方形花园,在上面修了一条道路,路的宽都是1米,其余部分种上各种花草,则种植花草的面积是平方米. 17. 《孙子算经》是中国古代重要的数学著作,成书大约在一千五百年前.书中记载了一个数学问题:“今有木,不知长短.引绳度之,余绳四尺五寸;屈绳量之,不足一尺.木长几何?”其大意是:“用一根绳子去量一根长木,绳子还剩余4.5尺;将绳子对折再量长木,绳子比长木短1尺,问长木多少尺?”设绳长尺,木长尺,可列方程组为 .18. 在平面直角坐标系中,若一个多边形的顶点都在格点(点的横、纵坐标均为整数)上,则称该多边形为格点多边形.格点多边形的面积记为S,其内部的格点数记为 , 边界上的格点数记为 . 如图,是格点三角形,对应的 , , .
17. 《孙子算经》是中国古代重要的数学著作,成书大约在一千五百年前.书中记载了一个数学问题:“今有木,不知长短.引绳度之,余绳四尺五寸;屈绳量之,不足一尺.木长几何?”其大意是:“用一根绳子去量一根长木,绳子还剩余4.5尺;将绳子对折再量长木,绳子比长木短1尺,问长木多少尺?”设绳长尺,木长尺,可列方程组为 .18. 在平面直角坐标系中,若一个多边形的顶点都在格点(点的横、纵坐标均为整数)上,则称该多边形为格点多边形.格点多边形的面积记为S,其内部的格点数记为 , 边界上的格点数记为 . 如图,是格点三角形,对应的 , , . (1)、图中格点四边形对应的S为;(2)、已知格点多边形的面积可以表示为 , 其中 , 为常数.若某格点多边形对应的 , , 则 .
(1)、图中格点四边形对应的S为;(2)、已知格点多边形的面积可以表示为 , 其中 , 为常数.若某格点多边形对应的 , , 则 .三、解答题
-
19. 计算:20. 解方程组21. 解不等式组: , 并求出它的整数解.22. 请将下面的证明过程补充完整:
如图,在四边形中, , , , 的角平分线交于点 , 求证: .
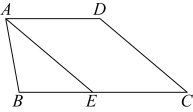
证明:∵平分 , (已知),
∴( ).
∵(已知),
∴ ▲ ( ).
∵(已知),
∴ ▲ (等量代换).
∴( ).
23. 一个数值转换器如图所示: (1)、当输入的值为16时,输出的值是;(2)、若输入有效的值后,始终输不出值,则所有满足要求的的值为;(3)、若输出的值是 , 请直接写出两个满足要求的的值.24. 如图,三角形的顶点坐标分别为 , , . 若将三角形向右平移4个单位长度,再向下平移3个单位长度得到三角形 , 其中点 , , 分别是点 , , 的对应点.
(1)、当输入的值为16时,输出的值是;(2)、若输入有效的值后,始终输不出值,则所有满足要求的的值为;(3)、若输出的值是 , 请直接写出两个满足要求的的值.24. 如图,三角形的顶点坐标分别为 , , . 若将三角形向右平移4个单位长度,再向下平移3个单位长度得到三角形 , 其中点 , , 分别是点 , , 的对应点. (1)、画出三角形;(2)、若三角形内有一点经过上述平移后的对应点为 , 写出点的坐标:( , );(3)、若点在轴上且三角形的面积为4,直接写出点的坐标.25. 图为国家节水标志,节水标志各部分的含义为:灰色的圆形代表地球,标志留白部分像一只手托起一滴水,手又像一条蜿蜒的河流,象征滴水汇成江河.某市在实施居民用水定额管理前,对居民生活用水情况进行了调查,通过简单随机抽样调查获得了50个家庭去年的月均用水量(单位:吨).以下是整理数据后的不完整统计表、统计图.
(1)、画出三角形;(2)、若三角形内有一点经过上述平移后的对应点为 , 写出点的坐标:( , );(3)、若点在轴上且三角形的面积为4,直接写出点的坐标.25. 图为国家节水标志,节水标志各部分的含义为:灰色的圆形代表地球,标志留白部分像一只手托起一滴水,手又像一条蜿蜒的河流,象征滴水汇成江河.某市在实施居民用水定额管理前,对居民生活用水情况进行了调查,通过简单随机抽样调查获得了50个家庭去年的月均用水量(单位:吨).以下是整理数据后的不完整统计表、统计图.
月均用水量频数分布表
分组
频数
4
12
9
5
4
2
合计
50

请根据图表中提供的信息解答下列问题:(1)、表中的值为 , 请补全频数分布直方图;(2)、扇形统计图中,月均用水量为“E:”的扇形的圆心角是°;(3)、为了鼓励节约用水,要确定一个用水量的标准,超出这个标准的部分按1.5倍价格收费.若要使的家庭水费支出不受影响,你觉得家庭月均用水量应该定为多少?为什么?26. 已知,直线 , 点为直线上一定点,射线交于点 , 平分 , . (1)、如图1,当时,°;(2)、点为线段上一定点,点为直线上的一动点,连接 , 过点作交直线于点 .
(1)、如图1,当时,°;(2)、点为线段上一定点,点为直线上的一动点,连接 , 过点作交直线于点 .①如图2,当点在点右侧时,求与的数量关系;
②当点在直线上运动时,的一边恰好与射线平行,直接写出此时的度数(用含的式子表示).
27. 围棋,起源于中国,古代称为“弈”,是棋类鼻祖,距今已有4000多年的历史.某商家销售A、B两种材质的围棋,每套进价分别为200元、170元,下表是近两个月的销售情况:销售时段
销售数量
销售收入
A种材质
B种材质
第一个月
3套
5套
1800元
第二个月
4套
10套
3100元
(1)、求A、B两种材质的围棋每套的售价.(2)、若商家准备用不多于5400元的金额再采购A、B两种材质的围棋共30套,求A种材质的围棋最多能采购多少套?(3)、在(2)的条件下,商店销售完这30套围棋能否实现利润为1300元的目标?请说明理由.28. 在平面直角坐标系中,对于点 , 点 , 定义与中的值较大的为点 , 的“绝对距离”.记为 . 特别地,当时,规定 , 例如,点 , 点 , 因为 , 所以点 , 的“绝对距离”为 , 记为 . (1)、已知点 , 点为轴上的一个动点.
(1)、已知点 , 点为轴上的一个动点.①若 , 求点的坐标;
②的最小值为;
③动点满足 , 所有动点组成的图形面积为64,请直接写出的值 .
(2)、对于点 , 点 , 若有动点 , 使得 , 请直接写出的取值范围.