北京市海淀区2022-2023学年七年级下学期数学期末考试试卷
试卷更新日期:2023-07-28 类型:期末考试
一、单选题
-
1. 下列图案中,可以由一个基本图形通过平移得到的是( )A、
 B、
B、 C、
C、 D、
D、 2. 如图,一条数轴被污渍覆盖了一部分,把下列各数表示在数轴上,则被覆盖的数可能为( )
2. 如图,一条数轴被污渍覆盖了一部分,把下列各数表示在数轴上,则被覆盖的数可能为( ) A、 B、 C、 D、3. 若是关于x,y的二元一次方程的一个解,则的值为( )A、 B、1 C、 D、24. 已知 , 下列变形中,一定正确的是( )A、 B、 C、 D、5. 小明一家在自驾游时,发现某公路上对行驶汽车的速度有如下规定,设此段公路上小客车的速度为千米小时,则满足的条件是( )
A、 B、 C、 D、3. 若是关于x,y的二元一次方程的一个解,则的值为( )A、 B、1 C、 D、24. 已知 , 下列变形中,一定正确的是( )A、 B、 C、 D、5. 小明一家在自驾游时,发现某公路上对行驶汽车的速度有如下规定,设此段公路上小客车的速度为千米小时,则满足的条件是( )最高限速
小客车

120
大型客车

100
货车

90
最低限速
60
A、 B、 C、 D、6. 如图,直线与交于点O, , 若 , 则的度数为( )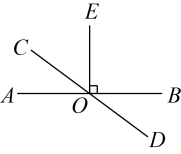 A、 B、 C、 D、7. 不等式的解集在数轴上表示为( )A、
A、 B、 C、 D、7. 不等式的解集在数轴上表示为( )A、 B、
B、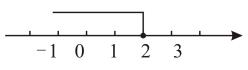 C、
C、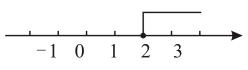 D、
D、 8. 将一个长方形的长减少 , 宽变成现在的2倍, 就成为了一个正方形, 设这个长方形的长为 , 宽为 , 则下列方程中正确的是( )A、 B、 C、 D、9. 如图,点A,B,C,D,E,F,G为正方形网格图中的7个格点.建立平面直角坐标系,使点B,C的坐标分别为和 , 则上述7个点中在第二象限的点有( )
8. 将一个长方形的长减少 , 宽变成现在的2倍, 就成为了一个正方形, 设这个长方形的长为 , 宽为 , 则下列方程中正确的是( )A、 B、 C、 D、9. 如图,点A,B,C,D,E,F,G为正方形网格图中的7个格点.建立平面直角坐标系,使点B,C的坐标分别为和 , 则上述7个点中在第二象限的点有( ) A、4个 B、3个 C、2个 D、1个10. 为了解北京市城乡居民可回收物投放情况和资源化利用情况,北京市统计局连续两年分别对全市16区的各3210名城乡居民开展调研,其中对于“被访者处理废弃电器及电子产品的方式(被访者回答时可以多选)”这一问题的答题统计如下图所示,图中的数据为选择该选项的人数占总调研人数的百分比:
A、4个 B、3个 C、2个 D、1个10. 为了解北京市城乡居民可回收物投放情况和资源化利用情况,北京市统计局连续两年分别对全市16区的各3210名城乡居民开展调研,其中对于“被访者处理废弃电器及电子产品的方式(被访者回答时可以多选)”这一问题的答题统计如下图所示,图中的数据为选择该选项的人数占总调研人数的百分比:
根据上述信息,以下说法中不合理的是( )
A、北京市城乡居民处理废弃电器及电子产品方式多样,呈现出多元化 B、在2022年,将废弃电器及电子产品闲置在家的被访者较2021年明显减少 C、与2021年相比,2022年“以旧换新”成为处理废弃电器及电子产品的最主要方式 D、在2022年,有不足1000名被访者选择了“旧货交易、二次出售”的处理方式二、填空题
-
11. 16的算术平方根是12. 计算 .13. 如图,由可以判定 , 其理由是 .
 14. 在平面直角坐标系中,若点到轴的距离是3,则的值是 .15. 有一个两位数,它的个位上的数为 , 十位上的数为 , 那么这个两位数可以用含有a,b的式子表示为 , 如果将它个位和十位上的数对调,使得到的两位数比原来的两位数大,那么a,b的大小关系为 .16. 如图,在平面直角坐标系中,已知点 , , 将线段平移,得到线段(点A的对应点为点 , 点的对应点为点),线段上任一点在平移后的对应点为 , 其中 , .
14. 在平面直角坐标系中,若点到轴的距离是3,则的值是 .15. 有一个两位数,它的个位上的数为 , 十位上的数为 , 那么这个两位数可以用含有a,b的式子表示为 , 如果将它个位和十位上的数对调,使得到的两位数比原来的两位数大,那么a,b的大小关系为 .16. 如图,在平面直角坐标系中,已知点 , , 将线段平移,得到线段(点A的对应点为点 , 点的对应点为点),线段上任一点在平移后的对应点为 , 其中 , . (1)、若点与点恰好重合,则 , ;(2)、若 , 且平移后三角形的面积最大,则此时 , .
(1)、若点与点恰好重合,则 , ;(2)、若 , 且平移后三角形的面积最大,则此时 , .三、解答题
-
17. 解下列方程组:(1)、(2)、18. 解不等式组:19. 已知正实数的两个平方根分別是和 .(1)、若 , 求的值;(2)、若 , 求的值.20. 如图,在平面直角坐标系中,已知点 , .
 (1)、线段的长为 , 请选用合适的工具,描出点的位置;(2)、若点的纵坐标为1,且 , 请判断:点的位置(填“唯一”或“不唯一”),若唯一,请说明理由;若不唯一,请在图中标出所有点的位置.21. 某博物馆有A,B两种不同的文创纪念品,花费400元可以购买10件A纪念品和4件B纪念品,或者购买5件A纪念品和10件B纪念品.(1)、A,B两种纪念品的单价各多少元?(2)、如果想购买两种纪念品共20件,其中A纪念品不少于8件,最少花费多少元?请说明理由.22. 如图,已知 , .
(1)、线段的长为 , 请选用合适的工具,描出点的位置;(2)、若点的纵坐标为1,且 , 请判断:点的位置(填“唯一”或“不唯一”),若唯一,请说明理由;若不唯一,请在图中标出所有点的位置.21. 某博物馆有A,B两种不同的文创纪念品,花费400元可以购买10件A纪念品和4件B纪念品,或者购买5件A纪念品和10件B纪念品.(1)、A,B两种纪念品的单价各多少元?(2)、如果想购买两种纪念品共20件,其中A纪念品不少于8件,最少花费多少元?请说明理由.22. 如图,已知 , . (1)、求证:;(2)、连接 , 恰好满足平分 . 若 , , 求的度数.23. 某市在实施居民阶梯电价收费政策前,对居民生活用电情况进行了调查,下图是通过简单随机抽样调查获得的50个家庭去年的月均用电量直方图:(数据分为如下5组, , , , , . )
(1)、求证:;(2)、连接 , 恰好满足平分 . 若 , , 求的度数.23. 某市在实施居民阶梯电价收费政策前,对居民生活用电情况进行了调查,下图是通过简单随机抽样调查获得的50个家庭去年的月均用电量直方图:(数据分为如下5组, , , , , . ) (1)、请补全直方图;(2)、根据直方图可以判断,在上面5个组中,月均用电量(度)在范围内的家庭最多;(3)、为鼓励节约用电,需要确定一个用电量的标准,将原来单一的的电费标准改为按月均用电量分为三档,如下表所示:
(1)、请补全直方图;(2)、根据直方图可以判断,在上面5个组中,月均用电量(度)在范围内的家庭最多;(3)、为鼓励节约用电,需要确定一个用电量的标准,将原来单一的的电费标准改为按月均用电量分为三档,如下表所示:档位
月均用电量(度)
电费单价()
第一档
第二档
第三档
①根据表中信息,需要按第三档标准缴纳电费的家庭数约占总家庭数的百分比为;
②抽样结果中,月均用电量为的9个家庭其月均用电量依次为 , , , , , , , , , 根据上述信息,若要使约的家庭电费支出不受到影响,请写出一个合理的值为 .
24. 对于两个关于的不等式,若有且仅有一个整数使得这两个不等式同时成立,则称这两个不等式是“互联”的.例如不等式和不等式是“互联”的.(1)、请判断不等式和是否是“互联”的,并说明理由;(2)、若和是“互联”的,求的最大值;(3)、若不等式和是“互联”的,直接写出的取值范围.25. 如图,已知线段 , 点是线段外一点,连接 , . 将线段沿平移得到线段 . 点是线段上一动点,连接 , . (1)、依题意在图1中补全图形,并证明:;(2)、过点C作直线 . 在直线上取点 , 使 .
(1)、依题意在图1中补全图形,并证明:;(2)、过点C作直线 . 在直线上取点 , 使 .①当时,画出图形,并直接用等式表示与之间的数量关系;
②在点运动的过程中,当点到直线的距离最大时,的度数是(用含的式子表示).
26. 在平面直角坐标系中,对于不重合的两点和点 , 如果当时,有;当时,有 , 则称点与点互为“进取点”.特别地,当时,点与点也互为“进取点”.已知点 , 点 . (1)、如图1,下列各点: , , , , 其中所有与点互为“进取点”的是;(2)、如果一个点的横、纵坐标都是整数,则称这个点为整点.在满足 , 的所有整点中(如图2):
(1)、如图1,下列各点: , , , , 其中所有与点互为“进取点”的是;(2)、如果一个点的横、纵坐标都是整数,则称这个点为整点.在满足 , 的所有整点中(如图2):①已知点为第一象限中的整点,且与点 , 点均互为“进取点”,求所有符合题意的点的坐标;
②在所有的整点中取个点,若这个点中任意两个点都互为“进取点”,直接写出的最大值.