河北省保定市曲阳县2022-2023学年七年级下学期7月期末数学试题
试卷更新日期:2023-07-28 类型:期末考试
一、单选题
-
1. 如下表,各式从左到右的变形中,是因式分解的有( )A、1个 B、2个 C、3个 D、4个2. 不等式 的解集在数轴上表示正确的是( )A、
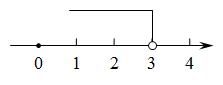 B、
B、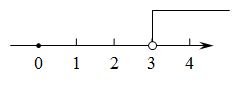 C、
C、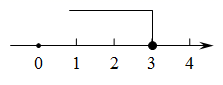 D、
D、 3. 小聪用100元钱去购买笔记本和钢笔共30件.已知每本笔记本2元,每支钢笔5元,小聪最多可以购买钢笔多少支?设小聪最多能买x支钢笔.可列出不等式( )A、 B、 C、 D、4. 如图,用四颗螺丝将不能弯曲的木条围成一个木框,不计螺丝大小,其中相邻两颗螺丝的距离依次为3、4、6、8,且相邻两根木条的夹角均可以调整,若调整木条的夹角时不破坏此木框,则任意两颗螺丝的距离的最大值是( )
3. 小聪用100元钱去购买笔记本和钢笔共30件.已知每本笔记本2元,每支钢笔5元,小聪最多可以购买钢笔多少支?设小聪最多能买x支钢笔.可列出不等式( )A、 B、 C、 D、4. 如图,用四颗螺丝将不能弯曲的木条围成一个木框,不计螺丝大小,其中相邻两颗螺丝的距离依次为3、4、6、8,且相邻两根木条的夹角均可以调整,若调整木条的夹角时不破坏此木框,则任意两颗螺丝的距离的最大值是( ) A、7 B、10 C、11 D、145. 如图为一张锐角三角形纸片ABC,小明想要通过折纸的方式折出如下线段:①BC边上的中线AD,②BC边上的角平分线AE,③BC边上的高AF.根据所学知识与相关活动经验可知:上述三条线中,所有能够通过折纸折出的有( )
A、7 B、10 C、11 D、145. 如图为一张锐角三角形纸片ABC,小明想要通过折纸的方式折出如下线段:①BC边上的中线AD,②BC边上的角平分线AE,③BC边上的高AF.根据所学知识与相关活动经验可知:上述三条线中,所有能够通过折纸折出的有( ) A、①② B、①③ C、②③ D、①②③6. 已知多项式x2+ax﹣6因式分解的结果为(x+2)(x+b),则a+b的值为( )A、﹣4 B、﹣2 C、2 D、47. 将-a2b-ab2提公因式-ab后,另一个因式是( )A、a+2b B、-a+2b C、-a-b D、a-2b8. 小明的作业本上有以下四题:① ;② ;③ ;④ .做错的题是( )A、① B、② C、③ D、④9. 利用两块完全一样的长方体木块测量一张桌子的高度,首先按图①所示的方式放置,再交换两木块的位置,按图②所示的方式放置.测量的数据如图,则桌子的高度等于( )
A、①② B、①③ C、②③ D、①②③6. 已知多项式x2+ax﹣6因式分解的结果为(x+2)(x+b),则a+b的值为( )A、﹣4 B、﹣2 C、2 D、47. 将-a2b-ab2提公因式-ab后,另一个因式是( )A、a+2b B、-a+2b C、-a-b D、a-2b8. 小明的作业本上有以下四题:① ;② ;③ ;④ .做错的题是( )A、① B、② C、③ D、④9. 利用两块完全一样的长方体木块测量一张桌子的高度,首先按图①所示的方式放置,再交换两木块的位置,按图②所示的方式放置.测量的数据如图,则桌子的高度等于( ) A、 B、 C、 D、10. 如图,将一块含有角的直角三角板的两个顶点放在长方形直尺的一组对边上,如果 , 那么的度数为( )
A、 B、 C、 D、10. 如图,将一块含有角的直角三角板的两个顶点放在长方形直尺的一组对边上,如果 , 那么的度数为( ) A、 B、 C、 D、11. 如果一个等腰三角形两边的长分别是1,5,那么它的周长是( )A、7 B、11 C、7或11 D、以上选项都不对12. 把多项式分解因式等于( )A、 B、 C、m(a-2)(m-1) D、m(a-2)(m+1)13. 不等式组的整数解是( )A、-1,0,1 B、0,1 C、-2,0,1 D、-1,114. 小明在抄因式分解的题目时,不小心漏抄了的指数,他只知道该数为不大于10的正整数,并且能利用平方差公式因式分解,他抄在作业本上的式子是 , 则这个指数的可能结果共有( )A、2种 B、3种 C、4种 D、5种15. 某班数学兴趣小组对不等式组讨论得到以下结论,其中正确的是( )
A、 B、 C、 D、11. 如果一个等腰三角形两边的长分别是1,5,那么它的周长是( )A、7 B、11 C、7或11 D、以上选项都不对12. 把多项式分解因式等于( )A、 B、 C、m(a-2)(m-1) D、m(a-2)(m+1)13. 不等式组的整数解是( )A、-1,0,1 B、0,1 C、-2,0,1 D、-1,114. 小明在抄因式分解的题目时,不小心漏抄了的指数,他只知道该数为不大于10的正整数,并且能利用平方差公式因式分解,他抄在作业本上的式子是 , 则这个指数的可能结果共有( )A、2种 B、3种 C、4种 D、5种15. 某班数学兴趣小组对不等式组讨论得到以下结论,其中正确的是( )①若 , 则不等式组的解集为;②若不等式组无解,则a的取值范围为;③若 , 则不等式组无解;④若不等式组只有两个整数解,则a的取值范围为
A、①②④ B、②③④ C、①②③ D、①③④16. 如图,在 中, ,将 沿直线 翻折,点 落在点 的位置,则 的度数是( ) A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
17. 两名同学将一个二次三项式因式分解,甲同学因看错了一次项系数而分解成;乙同学因看错了常数项而分解成 , 请你将原多项式写出并把因式分解正确的结果写出来: .18. 斑马线前“车让人”,反映了城市的文明程度,但行人一般都会在红灯亮起前通过马路.某人行横道全长24米,小明以的速度过该人行横道,行至处时,9秒倒计时灯亮了.小明要在红灯亮起前通过马路,他的速度至少要提高到原来的倍.19. 如图,和分别是的内角平分线和外角平分线,是的角平分线,是的角平分线,是的角平分线,是的角平分线,若 , 则 .

三、解答题
-
20. 计算:(1)、(用简便方法);(2)、(结果用科学记数法表示);(3)、(x-1)2-(x+1)(x-3).21. 解下列不等式(组),并把解集在数轴上表示出来:(1)、;(2)、 .22. 常用的分解因式的方法有提取公因式法、公式法,但有一部分多项式只单纯用上述方法就无法分解,如x2-2xy+y2-16,我们细心观察这个式子,会发现,前三项符合完全平方公式,进行变形后可以与第四项结合,再应用平方差公式进行分解.过程如下:x2-2xy+y2-16=(x-y)2一16=(x-y+4)(x-y-4)
这种分解因式的方法叫分组分解法.利用这种分组的思想方法解决下列问题:
(1)、9a2+4b2-25m2-n2+12ab+10mn;(2)、已知a、b、c分别是△ABC三边的长且2a2+b2+c2-2a(b+c)=0,请判断△ABC的形状,并说明理由.23. 如图,在ABC中,AE是边BC上的高线. (1)、若AD是BC边上的中线,AE=3cm, . 求DC的长.(2)、若AD是∠BAC的平分线,∠B=40°,∠C=50°,求∠DAE的大小.24. 某企业为保护环境,计划购置污水处理器,并在如下两个型号中选择:
(1)、若AD是BC边上的中线,AE=3cm, . 求DC的长.(2)、若AD是∠BAC的平分线,∠B=40°,∠C=50°,求∠DAE的大小.24. 某企业为保护环境,计划购置污水处理器,并在如下两个型号中选择:处理污水能力(吨/月)
价格(万元)
A型
240
10
B型
180
8
(1)、若计划处理污水2160吨,且均购置A型污水处理器,则需花费多少万元?(2)、若计划处理污水1920吨,同时购买两种型号的污水处理器,共花费82万元,则分别购买型污水处理器各多少台?(3)、该企业计划投入106万元全部用于购置两种污水处理器,且要求每月处理污水不少于2430吨,则购置A型处理器台.(直接写出答案)25. 如图,∠MON=90°,点A,B分别在射线OM,ON上运动,BE平分∠NBA,BE的反向延长线与∠BAO的平分线交于点C. (1)、当A,B移动后,∠BAO=45°时,则∠C= ;(2)、当A,B移动后,∠BAO=60°时,则∠C= ;(3)、由(1)、(2)猜想∠C是否随A,B的移动而发生变化?并说明理由.
(1)、当A,B移动后,∠BAO=45°时,则∠C= ;(2)、当A,B移动后,∠BAO=60°时,则∠C= ;(3)、由(1)、(2)猜想∠C是否随A,B的移动而发生变化?并说明理由.