河北省保定市高碑店市2022-2023学年七年级下学期7月期末数学试题
试卷更新日期:2023-07-28 类型:期末考试
一、单选题
-
1. 三边长的尺寸如图所示,则可能是( )
 A、1 B、2 C、10 D、162. 下列环保标志中是轴对称图形的是( )A、
A、1 B、2 C、10 D、162. 下列环保标志中是轴对称图形的是( )A、 B、
B、 C、
C、 D、
D、 3. 氧气是由氧元素形成的一种单质,氧元素的原子半径约为 , 则氧原子的半径用科学记数法表示为( )A、 B、 C、 D、4. 下列事件中,属于不可能事件的是( )A、打开电视,正在播“天空课堂” B、足球运动员射门一次,球进了 C、从一副扑克牌中随机抽取一张,抽到A D、投掷一枚正六面体的骰子,掷得朝上一面的点数恰好是75. 如图,要在一条主路旁建一座自来水中转站,向点处的小区引自来水,在什么地方建造,才能使输水管道最短?并说明理由.下列说法正确的是( )
3. 氧气是由氧元素形成的一种单质,氧元素的原子半径约为 , 则氧原子的半径用科学记数法表示为( )A、 B、 C、 D、4. 下列事件中,属于不可能事件的是( )A、打开电视,正在播“天空课堂” B、足球运动员射门一次,球进了 C、从一副扑克牌中随机抽取一张,抽到A D、投掷一枚正六面体的骰子,掷得朝上一面的点数恰好是75. 如图,要在一条主路旁建一座自来水中转站,向点处的小区引自来水,在什么地方建造,才能使输水管道最短?并说明理由.下列说法正确的是( ) A、点,两点之间线段最短 B、点,垂线段最短 C、点,两点确定一条直线 D、点,垂线段最短6. 计算的过程如下: . 步骤①,②分别表示的运算是( )A、幂的乘方,同底数幂相乘 B、积的乘方,同底数幂相乘 C、幂的乘方,乘法结合律 D、乘法交换律,合并同类项7. 使用尺规作线段的垂直平分线的痕迹如图所示,下列说法不正确的是( )
A、点,两点之间线段最短 B、点,垂线段最短 C、点,两点确定一条直线 D、点,垂线段最短6. 计算的过程如下: . 步骤①,②分别表示的运算是( )A、幂的乘方,同底数幂相乘 B、积的乘方,同底数幂相乘 C、幂的乘方,乘法结合律 D、乘法交换律,合并同类项7. 使用尺规作线段的垂直平分线的痕迹如图所示,下列说法不正确的是( ) A、弧①②的半径长一定相等 B、弧③④的半径长一定相等 C、弧②③的半径长一定相等 D、弧①的半径长大于长度的一半8. 一定能使等式“”成立的图形是( )A、
A、弧①②的半径长一定相等 B、弧③④的半径长一定相等 C、弧②③的半径长一定相等 D、弧①的半径长大于长度的一半8. 一定能使等式“”成立的图形是( )A、 B、
B、 C、
C、 D、
D、 9. 小亮设计了如下测量一池塘两端的距离的方案:先取一个可直接到达点 , 的点 , 连接 , , 延长至点 , 延长至点 , 使得 , , 再测出的长度,即可知道 , 之间的距离.他设计方案的理由是( )
9. 小亮设计了如下测量一池塘两端的距离的方案:先取一个可直接到达点 , 的点 , 连接 , , 延长至点 , 延长至点 , 使得 , , 再测出的长度,即可知道 , 之间的距离.他设计方案的理由是( ) A、 B、 C、 D、10. 在边长为的正方形纸片中剪下一个边长为的正方形,将剩余部分剪拼成一个长方形,尺寸如图所示,则“?”表示的长度为( )
A、 B、 C、 D、10. 在边长为的正方形纸片中剪下一个边长为的正方形,将剩余部分剪拼成一个长方形,尺寸如图所示,则“?”表示的长度为( ) A、 B、 C、 D、11. 将正方形网格图中的某两个白色方格涂上颜色,使整个图形有四条对称轴.正确的涂色位置是( )
A、 B、 C、 D、11. 将正方形网格图中的某两个白色方格涂上颜色,使整个图形有四条对称轴.正确的涂色位置是( ) A、①② B、①④ C、②③ D、①③12. 一副三角板 , 按如图所示的方式叠放在一起,其中 , , , 当时,( )
A、①② B、①④ C、②③ D、①③12. 一副三角板 , 按如图所示的方式叠放在一起,其中 , , , 当时,( ) A、 B、 C、 D、13. 毛毛的电子邮箱密码由八个数字或字母组合而成,其中每个数字都是从中任选的,毛毛只记得前七位的组合,第八位只记得是一个偶数,那么毛毛一次随机试验就能解锁密码的概率为( )A、 B、 C、 D、14. 地表以下岩层的温度随着所处深度的变化而变化,在某个地点与之间的关系可以近似地用关系式来表示.当深度增加时,的值( )A、减少 B、增加 C、不变 D、增加15. 如图,和是的高,交于点 , 且 , , 则的长为( )
A、 B、 C、 D、13. 毛毛的电子邮箱密码由八个数字或字母组合而成,其中每个数字都是从中任选的,毛毛只记得前七位的组合,第八位只记得是一个偶数,那么毛毛一次随机试验就能解锁密码的概率为( )A、 B、 C、 D、14. 地表以下岩层的温度随着所处深度的变化而变化,在某个地点与之间的关系可以近似地用关系式来表示.当深度增加时,的值( )A、减少 B、增加 C、不变 D、增加15. 如图,和是的高,交于点 , 且 , , 则的长为( ) A、3 B、4 C、5 D、616. 如图, , 点在上,且 , 点到射线的距离为 , 点在射线上, . 若的形状,大小是唯一确定的,则的取值范围是( )
A、3 B、4 C、5 D、616. 如图, , 点在上,且 , 点到射线的距离为 , 点在射线上, . 若的形状,大小是唯一确定的,则的取值范围是( ) A、或 B、 C、 D、或
A、或 B、 C、 D、或二、填空题
-
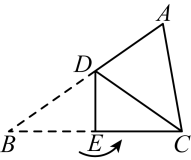
17. , 则 .18. 如图,将沿折叠,使点与点重合,若 , , 则 , .
 19. 将“
19. 将“ ”和“
”和“ ”按如图所示的方式有规律的排列.
”按如图所示的方式有规律的排列. (1)、图中“
(1)、图中“ ”的个数为7(填序号); (2)、设图中“
”的个数为7(填序号); (2)、设图中“ ”的个数为 , “
”的个数为 , “ ”的个数为 , 写出与的函数关系式为; (3)、若图中“
”的个数为 , 写出与的函数关系式为; (3)、若图中“ ”的个数与“
”的个数与“  ”的个数之和为247,则 .
”的个数之和为247,则 . 三、解答题
-
20.(1)、计算:;(2)、利用整式的乘法公式计算: .21. 已知 , , 求代数式的值.22. 如图,是的中线, , 分别是和延长线上的点,且 .
 (1)、与全等吗?请说明你的理由;(2)、若 , , 的面积为3,请直接写出的面积.23. 如图是一个可以自由转动的转盘,它被分成了6个面积相等的扇形区域.数学小组的学生做转盘试验:转动转盘,当转盘停止转动时,记录下指针所指区域的颜色,不断重复这个过程,获得数据如下:
(1)、与全等吗?请说明你的理由;(2)、若 , , 的面积为3,请直接写出的面积.23. 如图是一个可以自由转动的转盘,它被分成了6个面积相等的扇形区域.数学小组的学生做转盘试验:转动转盘,当转盘停止转动时,记录下指针所指区域的颜色,不断重复这个过程,获得数据如下:
转动转盘的次数
200
300
400
1000
1600
2000
转到黄色区域的频数
72
93
130
334
532
667
转到黄色区域的频率
0.36
0.325
0.3325
0.3335
(1)、下列说法错误的是(填写序号).①转动转盘8次,指针都指向绿色区域,所以第9次转动时指针一定指向绿色区域;
②转动15次,指针指向绿色区域的次数不一定大于指向黄色区域的次数;
③转动60次,指针指向蓝色区域的次数一定为10.
(2)、求表中 , 的值,并估计随机转动转盘“指针指向黄色区域”的概率(精确到0.1);(3)、修改转盘的颜色分布情况,使指针指向每种颜色的可能性相同,写出一种方案即可.24. 作图:如图, , 按以下步骤使用尺规作图(保留作图痕迹,不写作法):
①作的平分线;
②在上任意画出点E(不与点A重合);
③连接 .

问题:
(1)、说明平分的理由;(2)、判断与的数量关系,并说明理由.(提示:为说明方便,可直接在尺规作图后的图中添加字母或线段)25. 五月份正是杏大量上市的季节,小李将自家产的杏拿到集市上售卖,小李在卖杏之前,钱包内有零钱元,下表记录的是杏的销售额(元)随销售量(千克)变化的有关数据:销量(千克)
销售额(元)
请根据表中数据回答下列问题:
(1)、直接写出 , 值;(2)、求在小李售卖杏的过程中,钱包里的零钱(元)与(千克)的函数关系式;(3)、求销量为18千克时小李钱包中的零钱.26. 如图, , 点P在直线上,作 , 交于点M,点F是直线上的一个动点,连接 , 于点E,平分 . (1)、若点F在点E左侧且 , 求的度数;(2)、当点在线段(不与点M,E重合)上时,设 , 直接写出的度数(用含的代数式表示);(3)、将射线从(1)中的位置开始以每秒的速度绕点P逆时针旋转至的位置,转动的时间为t秒,求当t为何值时,为直角三角形.
(1)、若点F在点E左侧且 , 求的度数;(2)、当点在线段(不与点M,E重合)上时,设 , 直接写出的度数(用含的代数式表示);(3)、将射线从(1)中的位置开始以每秒的速度绕点P逆时针旋转至的位置,转动的时间为t秒,求当t为何值时,为直角三角形.