河北省承德市承德县2022-2023学年七年级下学期期末数学试题

试卷更新日期：2023-07-28 类型：期末考试

进入出卷网下载

一、单选题

1. 如图，在平面内作已知直线 $m$ 的平行线，可作平行线的条数有（）

A、0条 B、1条 C、2条 D、无数条

查看试题解析
2. 点P为直线l外一点，A，B，C三点在直线l上， $P A = 2.4 c m$ ， $P B = 3 c m$ ， $P C = 2 c m$ ，则点P到直线l的距离不可能是（）

A、 $2.4 c m$ B、 $2 c m$ C、 $1.5 c m$ D、 $0.8 c m$

查看试题解析
3. 微米是长度单位， $1 微米 = 0.000001 米$ ．已知人正常的红细胞的平均直径约为 $7.2$ 微米，用米做单位来表示这个数应为（）

A、 $7.2 \times 1 0^{6}$ B、 $72 \times 1 0^{- 7}$ C、 $7.2 \times 1 0^{- 6}$ D、 $0.72 \times 1 0^{- 5}$

查看试题解析
4. 下列计算正确的是（）

A、 $a^{3} + a^{4} = a^{7}$ B、 $a^{5} \div a^{2} = a^{3}$ C、 $3 a \cdot 2 a = 6 a$ D、 ${(- 3 m n)}^{2} = - 6 m^{2} n^{2}$

查看试题解析
5. 若 $a < b$ ，则下列不等式一定成立的是（）

A、 $a + c < b + c$ B、 $a c > b c$ C、 $a c^{2} < b c^{2}$ D、 $\frac{a}{c} > \frac{b}{c}$

查看试题解析
6. 如图，两直线a，b被直线l所截，则下列条件中不能证明 $a ∥ b$ 的是（）

A、 $∠ 1 = ∠ 5$ B、 $∠ 2 = ∠ 4$ C、 $∠ 3 = ∠ 5$ D、 $∠ 5 + ∠ 2 = 180 °$

查看试题解析
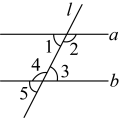7. 对于① $a^{2} b - a b^{2} = a b (a - b)$ ， ② $(x + 2) (x - 3) = x^{2} - x - 6$ ，从左到右的变形，下面的表述正确的是（）．

A、①②都是因式分解 B、①②都是乘法运算 C、①是因式分解，②是乘法运算 D、①是乘法运算，②是因式分解

查看试题解析
8. 在下列所给的四根已知长度的细木条中，能与长度为7cm，15cm的两根细木条首尾相接钉成一个三角形木架的是（）

A、7cm B、8cm C、13cm D、24cm

查看试题解析
9. 若 $(x - 3) (x + n) = x^{2} + m x - 21$ ，则m，n的值分别是（）

A、4， $- 3$ B、 $- 7$ ， 4 C、 $- 5$ ， 18 D、4，7

查看试题解析
10. 如图所示，下列关系一定成立的是（）

A、 $∠ A D B ＞ ∠ B E D$ B、 $∠ A E B ＞ ∠ D B C$ C、 $A E + A B ＞ B C$ D、 $∠ C ＞ ∠ A$

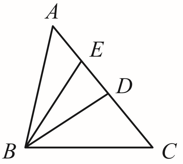查看试题解析
11. 在解二元一次方程组 ${\begin{array}{l} 6 x + m y = 3 ① \\ 2 x - n y = - 6 ② \end{array}$ 时，若 $① + ②$ 可直接消去未知数y，则m和n满足的条件是（）

A、 $m = 3 n$ B、 $m n = 1$ C、 $m + n = 0$ D、 $m - n = 0$

查看试题解析
12. 若关于x的一元一次不等式组 ${\begin{array}{l} x - 2 m < 0 \\ x + 1 \geq 2 \end{array}$ 无解，则m的取值范围为（）

A、 $m > - \frac{1}{2}$ B、 $m \leq \frac{1}{2}$ C、 $m > \frac{1}{2}$ D、 $m \leq - \frac{1}{2}$

查看试题解析
13. 如图，在边长为a的正方形中挖掉一个边长为b的小正方形，把余下的部分拼成一个长方形（无重叠部分），通过计算两个图形中阴影部分的面积，可以验证的一个等式是（）

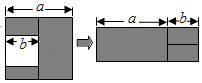A、a²﹣b²＝（a+b）（a﹣b） B、a（a﹣b）＝a²﹣ab C、（a﹣b）²＝a²﹣2ab+b² D、a（a+b）＝a²+ab

查看试题解析
14. 如图，将一副三角板和一张对边平行的纸条按下列方式摆放，两个三角板的一直角边重合，含 $30 °$ 角的直角三角板的斜边与纸条一边重合，含 $45 °$ 角的三角板的一个顶点在纸条的另一边上，则 $∠ 1$ 的度数是（）

A、 $10 °$ B、 $15 °$ C、 $40 °$ D、 $25 °$

查看试题解析
15. 一次学校智力竞赛中共有 $20$ 道题，规定答对一题得 $5$ 分，答错或不答一道题扣 $2$ 分，得分为 $75$ 分以上可以获得奖品，小锋在本次竞赛中获得了奖品．假设小锋答对了 $x$ 题，可根据题意列出不等式（）

A、 $5 x + 2 (20 - x) \geq 75$ B、 $5 x + 2 (20 - x) > 75$ C、 $5 x - 2 (20 - x) > 75$ D、 $5 x - 2 (20 - x) \geq 75$

查看试题解析
16. 如图，已知点P是射线 $O N$ 上一动点（不与点O重合）， $∠ O = 30 °$ ，若 $△ A O P$ 为钝角三角形，则 $∠ A$ 的取值范围是（）

A、 $0 ° < ∠ A < 60 °$ B、 $90 ° < ∠ A < 180 °$ C、 $0 ° < ∠ A < 30 °$ 或 $90 ° < ∠ A < 130 °$ D、 $0 ° < ∠ A < 60 °$ 或 $90 ° < ∠ A < 150 °$

查看试题解析

二、填空题

17. 已知：a^m=10，aⁿ=2，则a^m+n= .

查看试题解析
18. 如图，已知在 $△ A B C$ 中，点D，E，F分别为 $B C$ ， $A D$ ， $C E$ 的中点，且 $S_{△ A B C} ＝ 24 c m^{2}$ ，则 $S_{阴影} =$ $c m^{2}$ ．

查看试题解析
19. 为保证安全，某两段铁路 $M N ， P Q$ 两旁安置了两座可旋转探照灯A，B，探照灯的光线可看作射线如图，灯A的光线 $A C$ 从射线 $A M$ 开始，绕点A顺时针旋转至射线 $A N$ 上便立即回转，灯B光线 $B D$ 从射线 $B P$ 开始，绕点B顺时针旋转至射线 $B Q$ 便立即回转，两灯不停交叉照射巡视．已知 $P Q ∥ M N$ ，连接 $A B$ ， $∠ B A M ： ∠ B A N = 2 ： 1$ ，则 $∠ B A N =$ $°$ ；若灯B的光线先转动，每秒转动 $1 °$ ， 45秒后灯A的光线才开始转动，每秒转动 $2 °$ ，在灯B的光线第一次到达 $B Q$ 之前，灯A的光线转动秒时，两灯的光线互相平行．

查看试题解析

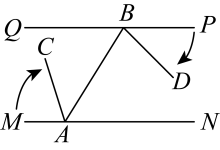
三、解答题

20.

(1)、解不等式组 ${\begin{array}{l} 3 (x + 1) \geq 2 x + 1 \\ 3 x < x + 2 \end{array}$ ．

(2)、已知 $4 x - 5 = 10$ ，求代数式 ${(x - 2)}^{2} - (x + 1) (x - 1)$ 值．

查看试题解析
21. 我们定义一个新运算，规定： $a ※ b = 4 a - 3 b$ ，例如： $5 ※ 6 = 4 \times 5 - 3 \times 6 = 2$ ，据此解答下列问题：

(1)、若 $x ※ y = 1$ ， $x ※ 2 y = - 2$ ，分别求出 $x$ 和 $y$ 的值；

(2)、若 $x$ 满足 $x ※ 2 \leq 0$ ，求 $x$ 的取值范围．

查看试题解析
22. 如图，方格纸中每个小正方形的边长都为1，在方格纸中将 $△ A B C$ 经过一次平移后得到 $△ A^{'} B^{'} C^{'}$ ，图中标出了点C的对应点 $C^{'}$ ．
⑴请画出平移后的 $△ A^{'} B^{'} C^{'}$ ；
⑵请连接 $A A^{'}$ ， $C C^{'}$ ，并直接写出这两条线段之间的位置关系和数量关系是 ▲ ；
⑶ $△ A^{'} B^{'} C^{'}$ 的面积为 ▲ ．

查看试题解析
23. 阅读理解：所谓完全平方式，就是对于一个整式 $A$ 如果存在另一个整式 $B$ ，使得 $A = B^{2}$ ，则称 $A$ 完全平方式．例如 $a^{4} = {(a^{2})}^{2}$ ， $a^{4} = {(a^{2})}^{2}$ ， $4 a^{2} - 4 a + 1 = {(2 a - 1)}^{2}$ ，则 $a^{4}$ ， $4 a^{2} - 4 a + 1$ 均为完全平方式．

(1)、下列各式中是完全平方式的是（只填序号）．
① $a^{6}$ ；② $a^{2} + a b + b^{2}$ ；③ $x^{2} - 10 x - 25$ ；④ $m^{2} + 6 m + 9$

(2)、将（1）中所选的完全平方式写成一个整式的平方的形式．

(3)、若 $x^{2} + x + m$ 是完全平方式，求 $m$ 的值．

查看试题解析
24. 已知 $A D$ 为 $△ A B C$ 的中线，E为线段 $A D$ 上一点．

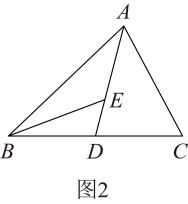
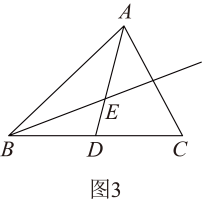(1)、如图1，若 $A B - A C = 3$ ， $△ A D C$ 周长为10，求 $△ A B D$ 周长；

(2)、若 $△ B D E$ 面积为20， $B D = 8$ ，请在图2中作 $△ B D E$ 的 $B D$ 边上的高，并求出点E到直线 $B C$ 的距离；

(3)、如图3，若 $∠ A B D = 40 °$ ， $∠ A D B = 110 °$ ，射线 $B E$ 平分 $∠ A B D$ ，点P射线 $B E$ 上一点，且直线 $D P$ 与 $△ B D E$ 的一条边所在的直线垂直，请直接写出 $∠ B D P$ 的度数．

查看试题解析
25. 某养鸡场计划购买甲、乙两种小鸡苗共2000只进行饲养，已知甲种小鸡苗每只2元，乙种小鸡苗每只3元．

(1)、若购买这批小鸡苗共用了4500元，求甲、乙两种小鸡苗各购买了多少只？

(2)、若购买这批小鸡苗的钱不超过4700元，问应选购甲种小鸡苗至少多少只？

(3)、相关资料表明：甲、乙两种小鸡苗的成活率分别为94%和99%，若要使这批小鸡苗的成活率不低于96%且买小鸡的总费用最小，问应选购甲、乙两种小鸡苗各多少只？总费用最小是多少元？

查看试题解析
26. 如图1，已知直线 $P Q / / M N$ ，点A在直线 $P Q$ 上，点C、D在直线 $M N$ 上，连接 $A C$ 、 $A D$ ， $∠ P A C = 50 °$ ， $∠ A D C = 30 °$ ， $A E$ 平分 $∠ P A D$ ， $C E$ 平分 $∠ A C D$ ， $A E$ 与 $C E$ 相交于E．

(1)、求 $∠ A E C$ 的度数；

(2)、若将图1中的线段 $A D$ 沿 $M N$ 向右平移到 $A_{1} D_{1}$ 如图2所示位置，此时 $A_{1} E$ 平分 $∠ A A_{1} D_{1}$ ， $C E$ 平分 $∠ A C D_{1}$ ， $A_{1} E$ 与 $C E$ 相交于 $E$ ， $∠ P A C = 50 °$ ， $∠ A_{1} D_{1} C = 30 °$ ，求 $∠ A_{1} E C$ 的度数．

(3)、若将图1中的线段 $A D$ 沿 $M N$ 向左平移到 $A_{1} D_{1}$ 如图3所示位置，其他条件与（2）相同，求此时 $∠ A_{1} E C$ 的度数．

查看试题解析