河北省保定市定兴县2022-2023学年七年级下学期7月期末数学试题
试卷更新日期:2023-07-28 类型:期末考试
一、单选题
-
1. 化简a2•a3的结果是( )A、a B、a5 C、a6 D、a82. 俗话说:“水滴石穿”,水滴不断的落在一块石头的同一位置,经过若干年后,石头上形成一个深度为的小洞,则用科学记数法可表示为( )A、 B、 C、 D、3. 若 , 则下列不等式一定成立的是:( )A、 B、 C、 D、4. 如图,生活中,有以下两个现象,对于这两个现象的解释,正确的是( )
 A、两个现象均可用两点之间线段最短来解释 B、现象1用垂线段最短来解释,现象2用经过两点有且只有一条直线来解释 C、现象1用垂线段最短来解释,现象2用两点之间线段最短来解释 D、现象1用经过两点有且只有一条直线来解释,现象2用垂线段最短来解释5. 对于① , ② , 从左到右的变形,表述正确的是( )A、都是因式分解 B、都是乘法运算 C、①是因式分解,②是乘法运算 D、①是乘法运算,②是因式分解6.
A、两个现象均可用两点之间线段最短来解释 B、现象1用垂线段最短来解释,现象2用经过两点有且只有一条直线来解释 C、现象1用垂线段最短来解释,现象2用两点之间线段最短来解释 D、现象1用经过两点有且只有一条直线来解释,现象2用垂线段最短来解释5. 对于① , ② , 从左到右的变形,表述正确的是( )A、都是因式分解 B、都是乘法运算 C、①是因式分解,②是乘法运算 D、①是乘法运算,②是因式分解6.某数学兴趣小组开展动手操作活动,设计了如图所示的三种图形,现计划用铁丝按照图形制作相应的造型,则所用铁丝的长度关系是( )
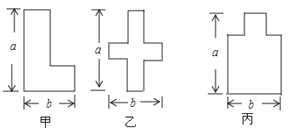 A、甲种方案所用铁丝最长 B、乙种方案所用铁丝最长 C、丙种方案所用铁丝最长 D、三种方案所用铁丝一样长7. 不等式组的解集在数轴上表示正确的是( )A、
A、甲种方案所用铁丝最长 B、乙种方案所用铁丝最长 C、丙种方案所用铁丝最长 D、三种方案所用铁丝一样长7. 不等式组的解集在数轴上表示正确的是( )A、 B、
B、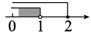 C、
C、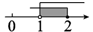 D、
D、 8. 若是二元一次方程的解,则的值为( )A、2 B、3 C、4 D、59. 下列多项式:① ;② ;③ ;④ ,其中能用平方差公式分解因式的多项式有( )A、1个 B、2个 C、3个 D、4个10. 若k为正整数,则 ( )A、 B、 C、 D、11. 若一个三角形的三边长是三个连续的自然数,其周长m满足10<m<20,则这样的三角形有( )A、2个 B、3个 C、4个 D、5个12. 如图,下列条件:①∠1=∠2;②∠4=∠5;③∠2+∠5=180°;④∠1=∠3;⑤∠6=∠1+∠2;其中能判断直线l1∥l2的有( )
8. 若是二元一次方程的解,则的值为( )A、2 B、3 C、4 D、59. 下列多项式:① ;② ;③ ;④ ,其中能用平方差公式分解因式的多项式有( )A、1个 B、2个 C、3个 D、4个10. 若k为正整数,则 ( )A、 B、 C、 D、11. 若一个三角形的三边长是三个连续的自然数,其周长m满足10<m<20,则这样的三角形有( )A、2个 B、3个 C、4个 D、5个12. 如图,下列条件:①∠1=∠2;②∠4=∠5;③∠2+∠5=180°;④∠1=∠3;⑤∠6=∠1+∠2;其中能判断直线l1∥l2的有( ) A、5个 B、4个 C、3个 D、2个13. 如图,直线 , 将含有的三角板的直角顶点放在直线上,若= , 则的度数是( )
A、5个 B、4个 C、3个 D、2个13. 如图,直线 , 将含有的三角板的直角顶点放在直线上,若= , 则的度数是( )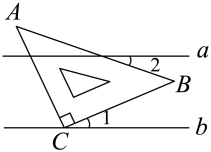 A、 B、 C、 D、14. 下面是两位同学在讨论一个一元一次不等式.根据上面对话提供的信息,他们讨论的不等式是( )
A、 B、 C、 D、14. 下面是两位同学在讨论一个一元一次不等式.根据上面对话提供的信息,他们讨论的不等式是( ) A、 B、 C、 D、15. 如图①,在边长为a的大正方形中剪去一个边长为b的小正方形,再将图中的阴影部分剪拼成一个长方形,如图②.这个拼成的长方形的长为30,宽为20,则图②中Ⅱ部分的面积是( )
A、 B、 C、 D、15. 如图①,在边长为a的大正方形中剪去一个边长为b的小正方形,再将图中的阴影部分剪拼成一个长方形,如图②.这个拼成的长方形的长为30,宽为20,则图②中Ⅱ部分的面积是( )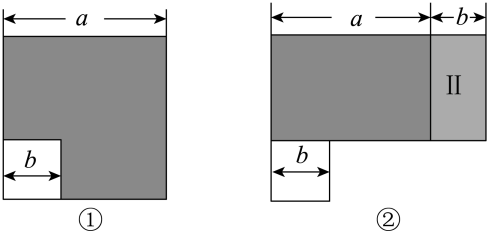 A、60 B、100 C、125 D、15016. 杨辉三角是数学之花,是中国古代数学的伟大成就.它有许多有趣的性质和用途,这个由数字排列成的三角形数就称为杨辉三角,如图,其中每一横行都表示 (此处 为自然数)的展开式中各项的系数.
A、60 B、100 C、125 D、15016. 杨辉三角是数学之花,是中国古代数学的伟大成就.它有许多有趣的性质和用途,这个由数字排列成的三角形数就称为杨辉三角,如图,其中每一横行都表示 (此处 为自然数)的展开式中各项的系数.…
那么 展开式中第四项的系数为( )
 A、8 B、10 C、18 D、20
A、8 B、10 C、18 D、20二、填空题
-
17. 计算: .18. 若多项式a2b2+6ab+A是完全平方式,则A= .19. 如图1,有一条长方形纸带ABCD,∠DEF=15°.
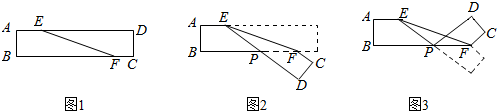 (1)、将纸带沿EF折叠,如图2所示,则∠EPB的度数为;(2)、将图2中的纸带再沿BF折叠,如图3所示,则∠CFE的度数为 .
(1)、将纸带沿EF折叠,如图2所示,则∠EPB的度数为;(2)、将图2中的纸带再沿BF折叠,如图3所示,则∠CFE的度数为 .三、解答题
-
20. 解方程组:21. 下面一道例题及部分解答过程,其中 、 是两个关于 , 的二项式.
例题:先去括号,再合并同类项
2(A)-3(B)
解:原式=
=( )
注意:运算顺序从左到右,逐个去掉括号
请仔细观察上面的例题及解答过程,完成下列问题:
(1)、直接写出多项式 和 ,并求出该例题的运算结果;(2)、求多项式 与 的平方差.22. 把下面的证明补充完整.如图,已知直线分别交直线于点平分平分 . 求证:

证明:(已知)
( )
平分平分(已知),
▲ , ▲ ( ),
▲ (等量代换)
( )
23. 如图,是一个长为2m,宽为2n的长方形,沿图中虚线用剪刀均分成四块小长方形,然后按图b的形状拼成一个正方形.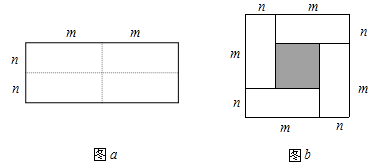 (1)、你认为图b中的阴影部分的正方形的边长等于多少?
(1)、你认为图b中的阴影部分的正方形的边长等于多少?答:
(2)、请用两种不同的方法求图b中阴影部分的面积.方法1:
方法2:
(3)、仔细观察图b,写出下列三个代数式之间的等量关系.代数式:(m+n)2 , (m-n)2 , 4mn
答:
(4)、根据(3)题中所写的等量关系,解决如下问题.若a+b=8,ab=5,则(a-b)2 = .
24. 如图,已知BC平分∠ABD交AD于点E , ∠1=∠3, (1)、证明;AB∥CD(2)、若AD⊥BD于点D , ∠CDA=34°,求∠3的度数.25. 某小区准备新建50个停车位,用以解决小区停车难的问题.已知新建1个地上停车位和1个地下停车位共需0.6万元;新建3个地上停车位和2个地下停车位共需1.3万元.(1)、该小区新建1个地上停车位和1个地下停车位各需多少万元?(2)、该小区的物业部门预计投资金额超过12万元而不超过13万元,那么共有哪几种建造停车位的方案?26. 综合与实践课上,同学们以“一个含30°角的直角三角尺和两条平行线”为背景开展数学活动,如图,已知两直线a,b且ab,三角形ABC中,∠ACB=90°,∠ABC=60° ∠BAC=30°.操作发现:
(1)、证明;AB∥CD(2)、若AD⊥BD于点D , ∠CDA=34°,求∠3的度数.25. 某小区准备新建50个停车位,用以解决小区停车难的问题.已知新建1个地上停车位和1个地下停车位共需0.6万元;新建3个地上停车位和2个地下停车位共需1.3万元.(1)、该小区新建1个地上停车位和1个地下停车位各需多少万元?(2)、该小区的物业部门预计投资金额超过12万元而不超过13万元,那么共有哪几种建造停车位的方案?26. 综合与实践课上,同学们以“一个含30°角的直角三角尺和两条平行线”为背景开展数学活动,如图,已知两直线a,b且ab,三角形ABC中,∠ACB=90°,∠ABC=60° ∠BAC=30°.操作发现: (1)、如图1,若∠1=42°,求∠2的度数;(2)、小聪同学把图1中的直线a向上平移得到如图2,请你探究图2中的∠1与∠2的数量关系,并说明理由.(3)、小颖同学将图2中的直线b向上平移得到图3,若∠2=4∠1,求∠1的度数.
(1)、如图1,若∠1=42°,求∠2的度数;(2)、小聪同学把图1中的直线a向上平移得到如图2,请你探究图2中的∠1与∠2的数量关系,并说明理由.(3)、小颖同学将图2中的直线b向上平移得到图3,若∠2=4∠1,求∠1的度数.